《自然数中的明珠》序

孙宏安

随笔与书评

《自然数中的明珠》序

孙宏安

与俞晓群相识有年，常有书籍上学习上的交往。欣闻晓群的著作《自然数中的明珠》要修订再版，我当然是很高兴的，因为这本书对我有很重要的意义——当年它的首版不仅使我了解了数论中的许多知识和典故，而且使我喜欢上了书中阐述的若干课题，在此后很长的岁月里对其研究的发展进行跟踪，并且在向中学数学教师和其他读者介绍相关的知识方面做了一些努力。不过当晓群发来修订稿要我先看一下并为之写一篇序的时候，我当真是亦喜亦忧了一番。喜的是能够先睹为快，了解那些我喜欢的课题的最新发展，忧的是对于我来说，这本书的序是如何可能呢？

回想起来，最初结识俞晓群是在二十世纪八十年代初，当时我协助我的导师梁宗巨和王鸿钧编写一部书《中学数学教师手册》，这部书就是俞晓群主持的编辑室编辑的。于是认识了晓群，可能由于我们最初都是学习数学的，所以有较多的共同语言，来往就多了起来，以这部书为起点，在晓群那里学习到许多著书立说的要点和书籍由组稿到撰写到编校到发排发行的全过程，这些对我后来的写作生涯无疑有着重要的奠基意义。晓群对于出版、书籍特别是文化的独到见解对于我提升自己的文化素养更有着潜移默化的作用，一个最典型的例子就是对中国古代科学的理解。由于我从事的专业工作特别是由于我的个人方面的因素我的研究一度指向中国古代科学和科学教育，特别是中国古代科学教育史。在进行了一些理论准备和大量的资料收集之后，我对中国古代科学教育史的研究就面临着这样两个问题：一个是按着什么样的方法论原则组织材料进行写作的问题，一个是如何处理中国古代文献中随处可见的数术的问题。

按我当时的理解，我们在探讨科学史时，通常是从现代科学出发，通过追溯其产生的渊源或以它“截取”古代文献中的模拟物进行研究。在研究中把古人的知识分解并解释为我们要研究的各门学科的成绩，可以称之为 “截取-解释”的方法论。这一点可能是十分必要的，否则我们就无法进入古代科学的殿堂。

正如西方科学史学科奠基人萨顿所说的“科学史是唯一能反映人类进步的历史”那样，许多科学史著述把科学的历史表述为科学成就的编年史，对中国科学史的研究也经常是这样。不可否认，这种研究是十分重要的，而且确已取得巨大的成就。但与此同时，人们又发现，这种“截取-解释”的研究，多是以现代科学为标准，用以截取中国古代的有关记载，然后予以现代科学的解释。这种方法论，当然有其意义。但是如果不考虑中国古人在从事有关活动时自己的目的和当时的社会价值观念，就可能陷入误区：或者，把所作的解释当作了中国古代文献中原来就有的东西，由此可以在中国古代文献中找出大批大批的西方科学要在数百年甚至上千年之后直至近代甚至现代才得出的科学成果，更有甚者，竟能在某些中国古代文献中发现现代的前沿科学成果；或者，不承认被解释项是解释项的某种特例，因而认为中国古代无科学。值得注意的是，这两种趋于极端的观点居然是在同一种方法论指导下得出来的。这提示我们，这种“截取-解释”的方法具有较大的随意性，因此仅仅采用这样的方法论原则是难以实现科学史研究的目的的，这一点当然对科学教育史的研究也具有同样的意义，因为科学教育是以科学为内容的，必须在正确评价某一时代科学的情况下才能正确评价当时的科学教育。我怎么办呢？

这时读到了俞晓群惠赠的著作《古数钩沉》（北京师范大学出版社），书中晓群提出了这样一个科学史研究的方法论原则：使科学史研究“进入一个更广阔的思维空间之中”，即“在大文化的背景下，探讨每一历史现象的存在和意义”，而“在文化人类学的意义上，历史是一个有机的整体，任何人为地割裂历史的做法都是违反科学精神的。对于历史事实的认识问题，其关键在于研究者的态度，而不在于保留些什么，抛弃些什么，掩盖些什么，或者篡改些什么。”这一方法论原则——可以称为“大文化背景分析”的原则——与前面说的“截取-解释”原则有很强的互补性。这两者的结合将有助于理解古代科学，因而也有助于科学史和科学教育史的研究和发展。这就解决了我的中国古代科学教育史研究的方法论原则的问题，我的研究迅速升温，很快就取得了预期的成果。

至于数术，那是无论探讨中国古代数学探讨中国古代科学或者更广泛的研究中国古代文化，都无法绕过去的坎儿，比方说，翻开《史记》，几乎每一篇都涉及到数术。但是当时所见的许多科学史甚至历史著作对数术都缺乏关注，或者说是回避或者部分回避数术问题。不过我却无法回避，因为在我的中国古代科学教育研究中，怎么处理数术甚至于决定着对古代科学教育的重要事实和评价的问题，因为我们通常用科学专门教育解释的事物，对古人来说可能是纯粹的数术教育！按照大文化背景分析的方法论，数术是中国古代一个相当独特的文化因素，必须正视它，研究它。俞晓群的《古数钩沉》就探讨了若干数术问题，他的一系列文章更专门探讨了中国文化中的数术，后来他出版了一部《数术探秘：数在中国古代的神秘意义》（生活·读书·新知三联书店）总结自己对数术的研究。对于数术研究，他充分发挥自己的哲学智慧，坚持研究数术的理性原则和对数术探索的大文化背景分析原则。再后来他又出版了一部《数与数术札记》（中华书局），对数术进行了更为深入的哲学和文化学分析，例如，在分析了《十三经》的数术特征之后，探讨了数术的产生和演化，探讨了徜徉在科学、非科学与伪科学之间的易数（一种“纯”的数术），特别是探讨了数术观念的力量。这部书 “是把解读数与数术古代典籍同哲学思考紧密结合在一起的”（王充闾语）。应该说，俞晓群是国内较早从科学的角度运用科学的方法对数术加以文化探讨、科学分析乃至于哲学思考的学者，他的这一思路后来得到学界的响应，《数术探秘》甚至产生了国际影响，我就见到过韩国出版的韩文译本。俞晓群的数术研究为我的中国古代科学教育史中对数术的分析提供了基础。而且使我对数术大感兴趣，后来还对《红楼梦》做了一点儿数术研究，形成了几篇文字。

由于方法论和数术理解这两个问题的解决，我顺利地完成了中国古代科学教育史的研究，提出的中国古代科学发展的文化背景——人文精神，治术精神和数术氛围——得到了若干人士的首肯，并借以申报了一项教育部重点课题，进而实现了对中国近现代科学教育史的研究。说起来，俞晓群的帮助对我的研究来说是非常重要的。

二十世纪九十年代初，俞晓群接手主持辽宁教育出版社的工作，后来担任辽宁出版集团副总，再后来任海豚出版社社长，逐渐成为一位著名的编辑和出版家，他提出并且努力实践着出好书构建“书香社会”的出版观念。看一下他主持的大书单：创作：“国学丛书”（二十种）、“当代汉学家论著译丛”、“中国地域文化丛书”、“书趣文丛”（六辑六十种）、“新世纪万有文库”、“万象书坊”、“海豚书馆”等。引进：《牛津少年儿童百科全书》和“牛津学术精选”（与英国牛津大学出版社合作，顺便说一下，俞晓群主持的辽宁教育出版社是较早与国外出版社实现合作的出版社之一），“剑桥集粹”、《工商管理大百科全书》、《经济学：原理与政策》和《投资组合与投资组合管理》（与美国ITP公司联合出版），与英国吉尼斯世界纪录有限公司签约，陆续出版发行了“吉尼斯”系列六种单卷本大型百科全书，之后又推出了举世瞩目的《吉尼斯世界纪录大全》（二〇〇〇、二〇〇一、二〇〇二、二〇〇三年版），还引进了“IDG傻瓜系列”、“完全傻瓜指导系列”和“袖珍傻瓜指导系列”、“几米作品精选集系列”、“美国国家地理学会旅行家系列”、“百年摄影经典系列”、“探索书系”、“美国国家地理杂志系列”、“古希腊、古罗马和欧洲风化史系列”、“科林斯精品系列”等精品图书。

进一步看一下正在运作的“海豚书馆”的详细书单：

我见到了十二辑五十一种，包括：

类别 书名 作者遗珠 周錬霞甘雨胡同六号 南 星八十回忆 熊式一文艺拾遗（二十三种）孽海花闲话 冒鹤亭武侠丛谈 钱基博高罗佩事辑 严晓星从莎士比亚说到梅兰芳 宋春舫兰生弟的日记 徐祖正

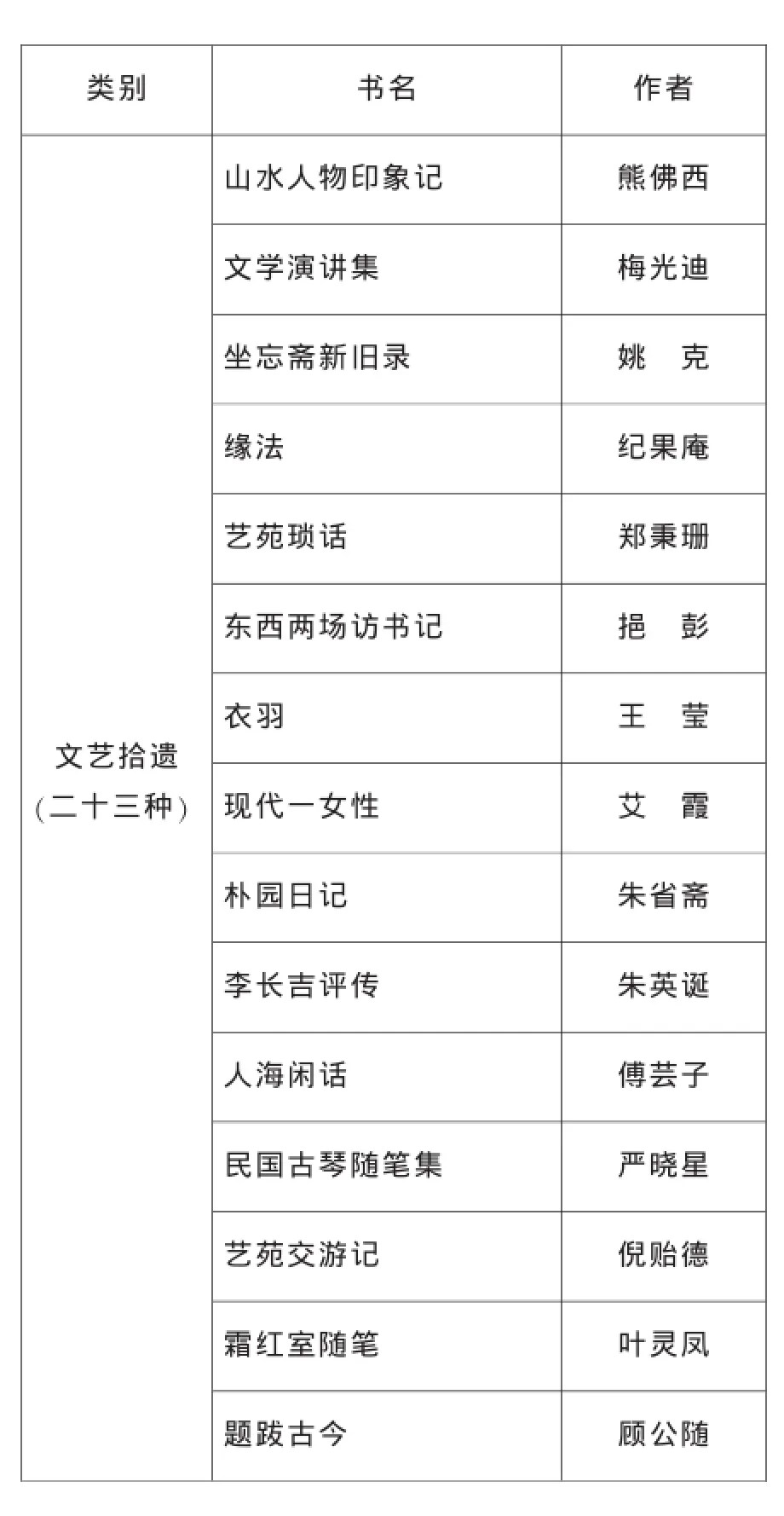
类别 书名 作者山水人物印象记 熊佛西文学演讲集 梅光迪坐忘斋新旧录 姚 克缘法 纪果庵艺苑琐话 郑秉珊东西两场访书记 挹 彭衣羽 王莹文艺拾遗（二十三种）现代一女性 艾 霞朴园日记 朱省斋李长吉评传 朱英诞人海闲话 傅芸子民国古琴随笔集 严晓星艺苑交游记 倪贻德霜红室随笔 叶灵凤题跋古今顾公随

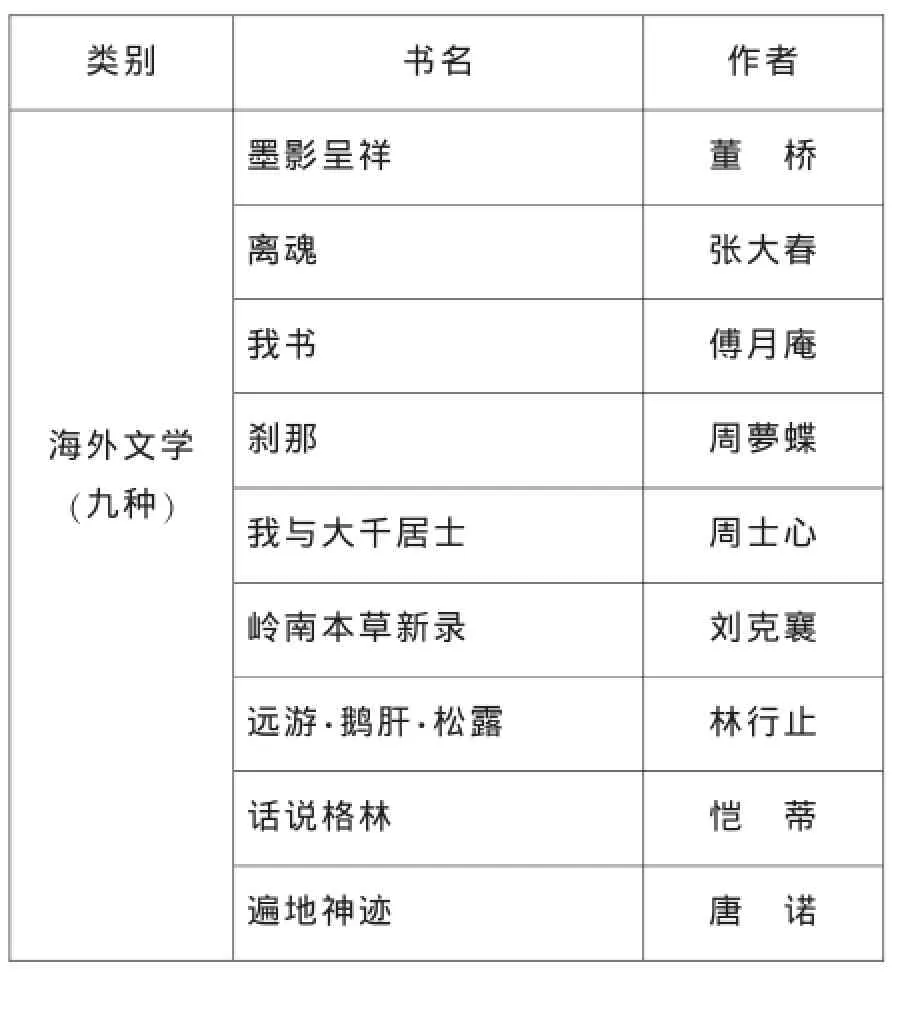
类别 书名 作者墨影呈祥 董桥离魂 张大春我书 傅月庵海外文学（九种）刹那 周夢蝶我与大千居士 周士心岭南本草新录 刘克襄远游·鹅肝·松露 林行止话说格林 恺蒂遍地神迹唐诺

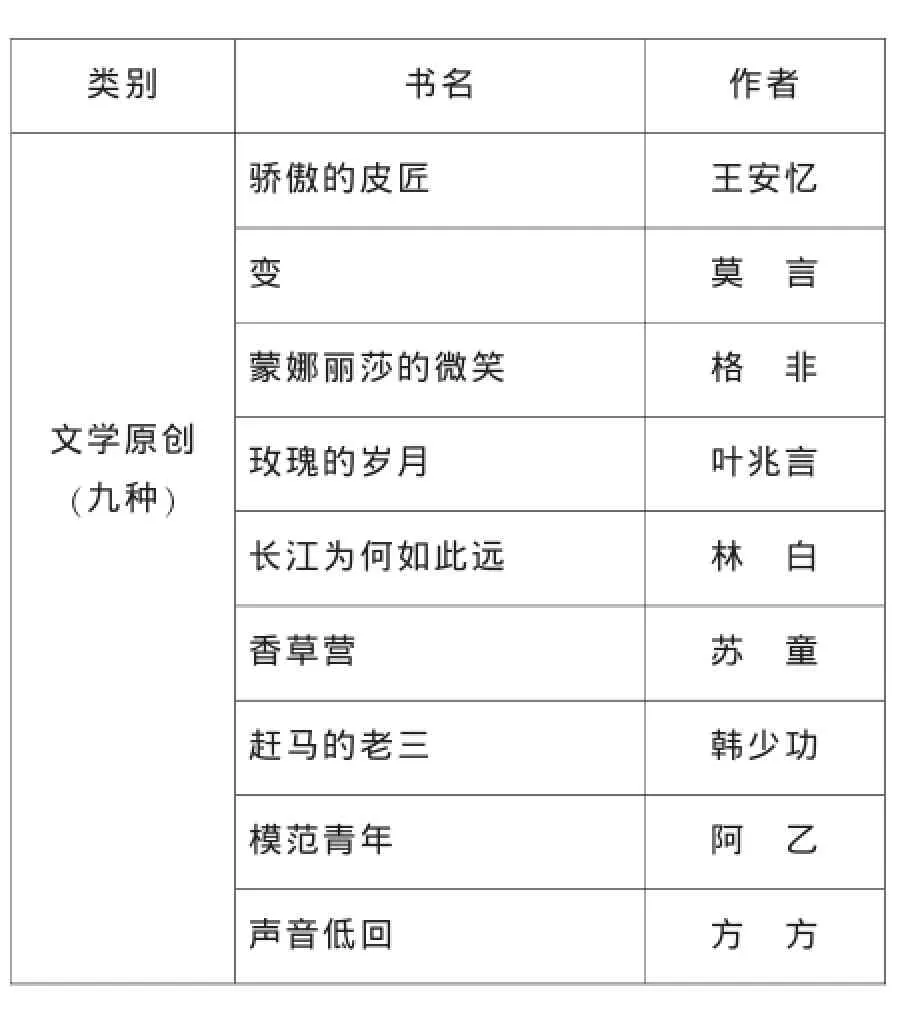
类别 书名 作者骄傲的皮匠 王安忆变莫言蒙娜丽莎的微笑 格 非文学原创（九种）玫瑰的岁月 叶兆言长江为何如此远 林 白香草营 苏童赶马的老三 韩少功模范青年 阿乙声音低回 方方

类别 书名 作者汉石经斋文存 徐森玉占卜的源流 容伊学术钩沉（五种） 中国坐椅习俗 翁同文汉字史话 李孝定中国历史上的纪年 刘乃和

类别 书名 作者胡诌诗集 爱德华·李尔翻译小品（二种） 法朗士私记 施康强

类别 书名 作者本无畛域——书评七篇 葛兆光学术原创（三种）历史意识与帝王意志 杨国强人文·民主·思想 余英时

出版社与学术研究是什么关系？透过俞晓群在辽宁教育出版社的工作，我深深地感到出版社是学术研究的重要阵地，在一些情况下甚至是学术研究的组织者和旗帜。就我所稍有涉猎的数学史和科学史领域来看，俞晓群主持的辽宁教育出版社在相当时期内就起了这样的阵地、组织者和旗帜的作用。看一下当时辽宁教育出版社的一份丛书的书单：

《中国古代科技名著译丛》、《自然科学大事记》（八种）、《中国古代科学技术事典》、《新世纪科学史系列》（七种）、《中国科学技术史纲》（六种）。

以前两种为例，《中国古代科技名著译丛》，选择了学界公认的二十几部中国古代科技名著，进行了文字校订、难点注释、全文白话翻译，每部书还要请相应的研究专家撰写导言，对该书进行全面的论述。这套丛书是对中国古代科学技术的一次相当规模的研究和普及，对中国科学技术史的研究产生了积极的促进作用。《自然科学大事记》别开生面的地方是把中国古代科学成果融入世界科学发展之中，编年体更有利于对中国古代科学在世界科学发展的背景下的认识和深入理解。

科学界和科学史界的知名人士诸如卢嘉锡、路甬祥、李学勤、梁宗巨、梅荣照、郭书春、陈美东、何丙郁、廖育群、江晓原、刘钝、李文林等都进入丛书作者的名单，充分表明这些丛书在科学史领域的前沿性和权威性。不仅如此，辽宁教育出版社还为科学史界学者的创新性研究开辟了阵地，就记忆所及，下面这些书在学界是产生了很大的影响的：《李俨钱宝琮科学史全集》，何丙郁《中国科技史论集》，陈美东《古历新探》，郭书春 《汇校九章算术》、《校点算经十书》，《严敦杰祖冲之科学著作校译》，梁宗巨《数学历史典故》、《世界数学通史》，刘钝、王扬宗《中国科学和科学革命》。

出版社与学术研究的关系实际上就是出版社与学者的关系，这个关系首先表现在两个方面，一个是出版社的学术研究作用就是通过作者学者群体现出来的，因此创造条件充分发挥学者的创造才能就是出版学术著作的题中应有之义；另一个是作者学者队伍的建设创新。这两个方面晓群他们处理得都是很好的，不仅为一些著名的学者出版了若干新著，而且这些丛书使一大批学术新秀走上前台推出自己的著作，后来其中不少人士成为有关领域的台柱。这个关系其次还表现在出版人与作者的关系方面，晓群在这方面的做法令人感动。主要是体现着“以人为本”的思想，及时与作者沟通，对作者尊重、关心、帮助，注意聆听作者的意见和建议，不仅如此，俞晓群和作者的关系还进入了思想交流、精神共鸣的境界。他在自己的著作《人书情未了：一个出版人的手记》（东方出版社）、《这一代的书香：三十年书业的人和事》（浙江大学出版社）中详细的记载和描述就表现出这一境界。俞晓群和我的导师梁宗巨的交往给我留下深刻的印象。

梁宗巨教授是数学史领域的领军人物之一，早年就从事世界数学史的研究，但是在众所周知的动乱年代里梁宗巨受到迫害，最初的巨量的手稿也被付之一炬。戏剧性的是当时的一位学生冒着危险 “偷出”两本手稿精心保存下来，一九七七年交还梁宗巨。梁宗巨一切从头开始，一九八〇年辽宁人民出版社出版了梁宗巨的《世界数学史简编》一书，这是国内研究世界数学史的开端。接着，辽宁教育出版社（就是从辽宁人民出版社中分出来的）和梁宗巨的合作就开始了，并且一直持续下去，俞晓群把这种合作提高到了新的层次，特别是优先考虑对梁宗巨一直从事的世界数学通史的研究撰写提供支持，作为重点图书出版了梁宗巨的阶段性成果《数学历史典故》（一九九二）；并请梁宗巨主持《自然科学大事记·数学卷》（一九九四），以此为梁宗巨的研究提供一个新的阵地；接着，就开始出版梁宗巨作为国家自然科学基金项目的 《世界数学通史》，一九九五年开始印行上卷，并应梁宗巨的修改要求，在刚刚印出后马上就修订改版一次，但是梁宗巨竟没能看到上卷的最后正式出版。是年底，梁宗巨因病辞世，留下下卷的写作提纲和近十万字的手稿。下卷怎么办？俞晓群毫不犹豫地接受了梁宗巨最后的安排，要我和他的第一位研究生王青建完成下卷的续写工作。随后，俞晓群委托专门的编辑，支持、鼓励，在一定程度上也是督促我们的续写工作，和我们一起摸爬滚打三年之久，终于完成了这一艰巨的工作，形成了八十万字的下卷，俞晓群马上决定同时出版重新设计的上下卷一体版本，以此来表示对本书的重视和对梁先生的纪念。当然这部书也不负众望，后来和辽宁教育出版社“新世纪科学史系列”之一——路甬祥的《科学之旅》一同入选中国出版集团的《中国文库》第二辑科学技术类之列。

多少年之后，俞晓群这样表述与梁宗巨的交往和对梁宗巨的怀念：

我问他，那本《世界数学史简编》为什么写得如此流畅，如此完美，甚至超越了学术专著固有范式的窠臼？他说，这里面包含着一个人生命的意义，还浸润着生活的泪水和血水……他再拿起笔，心中的学问已经化成一种宗教式的崇高与冲动。生活与生命的意义都被结成文化精神的力量，支撑着梁先生那支神来的妙笔。

我问他下一篇文章是什么？他说是《零的历史》。此文一发表，就轰动了数学史界。我问他下一部学术著作是什么？他说是《数学历史典故》。此书一出版，台湾九章出版社立即购买了它的繁体字版权。我问他再下一部著作是什么？他说是 《世界数学通史》。我们马上签下此书的出版合同、渴盼着这部巨著的完成……一九九五年十一月二十日，梁先生溘然仙逝。

记得一九九六年元旦的那天晚上，我打开自己的《编辑日记》，试图从“我的作者”栏目中划去梁先生的名字，禁不住热泪喷涌而出。后来，我这样感伤的情绪一直延续下去，直到《世界数学通史》上卷出版，直到梁先生的学生孙宏安、王青建接续完成下卷的写作，直到中国出版集团将这部大作收入“中国文库”，直到今天，我又一次伴看秋日的凉风斜雨，回望那一点书与人的往事……

每当读到此处，我都感到有热泪盈眶：梁宗巨的音容笑貌如在眼前，续写世界数学通史的场景历历在目。俞晓群对梁宗巨的尊重、向往、同情、怀念的浓重的感情使我感动，而且更深入地感受到俞晓群的人文情怀，我想这正是对“以人为本”思想的实践诠释。

回到《自然数中的明珠》这部书上来，认真阅读（其中一部分是重读），感到确实很有特色，主要表现为这样几点：

1、促进读者学思结合

这部书当然是一部数学科普著作，但是并不是完全以数学趣事吸引读者的，很多地方倒是以数学思维取胜——实际上数学思维是更本质的数学趣味。一个做法是对书中引用的命题，大多都给以运用初等方法的证明，这些证明和论述密切结合，能加强读者的数学思考。难能可贵的是，在一些简单的证明中，有的还为读者留下进一步思考的空间，而这些思考正好是理解下一步论述的需要。全书的安排例如对所讲述的八种数的关系的论述，也是促进读者进行学思结合的极好的方式——实际上使人不由自主地对这些数的关系作进一步的思考，并得出“原来如此”的思考后的感叹！

2、有特色的数学历史阐述

对于本书所论述的各种数，几乎都给出了详细的历史脉络，因此这部书又是一部数学史的科普著作，实际上所论述的各种数的提出研究和发展就是一个历史的过程，这一过程充分表明数学是人类共同的文化遗产，在每一种数的发展过程中许多国家许多民族的许多有名的和无名的数学家作出了自己的贡献。本书不是数学史的专门著述，但还是尽量指出有关学者的工作。当然，另一方面，正如本书在详细地阐述了勾股定理的发现和证明后指出关于最先发现和命名存在争议，然后作了评价：“用什么来命名并不是问题的关键，无论是谁最早发现的勾股定理，它都是全人类的财富。”这应该就是数学史以及科学史研究者的胸怀！

数学史的阐述离不开数学家，本书介绍了若干在所阐述的数的研究中起了重要作用的数学家的简短的传略，有可能的还附上了照片或者画像，这对于理解有关的数学知识的发展是颇有益处的。这方面本书的一个特点是对于数学大师的贡献予以充分的展示，但是并不拔高吹捧，而是也指出大师的失误；同时对于数学家偶尔出现的失误予以分析，但并不是吹毛求疵，而是力图找出失误产生的可能原因以及就是这个失误对数学的发展产生了什么积极的影响。在一定程度上“还原”数学研究的“原生态”。这一个方面充分表现出作者的辩证的发展的哲学的思维方式，对读者则有思考问题方式上的启发。

3、促进读者的整体性思维

如前面说的把所讨论的各种数联系起来的做法对人的思考的促进的一个方面就是对整体性思维的促进作用，而这种作用特别是在作者进行有关的历史阐述时表述出来，给人以特别深刻的印象。这也可以说是促进读者学思结合的一个具体内容。

书中引用高斯《算术研究》(一八〇一)中的话：“把素数同合数鉴别开来，以及将合数分解成素因数的乘积，被认为是算术中最重要最有用的问题之一。”可以说是本书“整体性”的纲要，实际上指出了素数判定，合数的因数分解，数的因数的种种关系，就是所有这八种数的本质性的联系。这一点儿也不奇怪，因为就是现代数学界也仍然认为“自然数结构的中心是素数”〔休森（S.F.Hewson），二〇〇四〕。

例如完全数是亲和数的一种特例：m和n是一对亲和数的充要条件是因数之和σ(m)=σ(n)= m+n。如果这个式子中m=n，则变成了σ(n)=2n，m=n就是一个完全数。

完全数和亲和数都是由某数的因数和引起的，数的因数和甚至各个数位上的数字之和都能构成新的数论话题，如“数的黑洞”问题——自生成数、自复制数、因数和的黑洞——都属于这种情况。

再如指出：鲁卡斯发现了斐波那契数列与梅森数的渊源。而通过斐波那契数系，又可以把斐波那契数与所有的自然数联系起来。

任何费马合数都是伪素数但都不是卡迈克尔数；费马合数的因数如果不是素数就一定是伪素数。这样就把伪素数与费马数联系起来了。

任意两个费马数都没有公因数，由它可推出“素数是无限多的”。得到了素数无限性的另一种证明：

费马数既不是完全数，也不是亲和数中的一个。

斐波那契数的方幂的展开式与二项展开式（贾宪三角）的相似性，形数与贾宪三角也有密切的关系，这个角度也表现出形数和斐波那契数的联系，而且斐波那契数通过黄金数与混沌也联系起来。

4、数论前沿成果介绍的及时性

数论是大众喜爱的数学课题，一些即使是非常前沿的数论课题其结果也往往是人人都可以明白的——这就是数论的魅力之所在：它的问题往往能够很简单地表述出来，但是解决起来（证明或者反驳）却极其困难；它的证明可能非常简单而精巧，也可能极其冗长和复杂。正因为如此，经常有大量的业余数学爱好者试图用非常简单的方法去解决数论中的著名问题。所以及时向公众介绍数论研究的前沿成果是很有必要的，这是数论方面的普及著作的重要内容之一。但是因为数论研究是每时每刻都散在地进行着的，因此追踪数论的某些课题的研究发展有一定的难度。所以常出现介绍数论的著述中所说的某课题“现在最好的成果”往往是很久以前的成果了，其结果不仅仅使读者得不到最新的信息，而且使这一著述在一定程度上失去可信度。这方面的例子不胜枚举。此外，研究者得出人家早已得出的成果的情况也是时常发生的。例如我在二〇〇五年的一个学术性期刊上看到一篇文章，说是找到了十对最大的亲合数，看一下还没有本书中指出的一九七四年的成果大；还有二〇一一年的一篇文章，十分努力地证明“费马数既不是完全数，也不是亲和数中的一个”，但是按本书的介绍，这个命题在二〇〇〇年已经为吕卡（Florian Luca）所证明。再如，看到一篇二〇〇七年的文字，论证费马数没有公因数认为得到了证明素数无限多的一个新证法。本书则十分注意数学成果的时间性（这就是数学史著述的特点），一些成果一直列举到二〇一二年八月，其余的成果也注意给出得到的时间，我想对于一个普及型著作这一点就更加重要，因为读者不可能深入研究有关的内容关注研究前沿的信息，为读者提供及时的前沿研究信息就是一个普及读物作者的责任。应该说，我特别认同本书的这个特点！

愿作为写作人的俞晓群写出更多的著作，愿作为出版人的晓群出版更多的好书。是为序。

二〇一二年仲秋

孙宏安，大连教育学院教授。