储层渗透性与地层因素关系的实验研究与分析

刘忠华，吴淑琴，杜宝会，李潮流，胡 松，曾富强

1中国石油勘探开发研究院测井与遥感技术研究所，北京 100083

2大港油田公司勘探事业部，天津 300280

1 引 言

阿奇1942年［1］给出了地层因素与孔隙度之间的函数表达式，同时他发现，与孔隙度相比，渗透率与地层因素的关系并不明晰，但他并未就此问题做进一步深入分析.一般认为，同孔隙度一样，渗透性与地层因素之间也呈负相关关系，即渗透性越差、含水岩石的导电能力越差，地层因素增加；渗透性越好、导电能力越好，地层因素减小［2－5］.但这一观点并未真正得到以大量配套岩芯实验数据为基础的证明（无论是来自不同地区还是来自同一地层）.在低渗透致密砂岩油气藏日益成为油气重点勘探领域的今天，搞清储层渗透性与地层因素的关系，对于正确理解低渗透致密砂岩储层的导电能力、提高利用电阻率测井资料识别评价低渗透油气藏精度具有重要意义.

为了揭示储层渗透性与地层因素之间的内在关系，本文对渤海湾盆地不同孔隙结构的碎屑岩储层样品进行了孔隙度、渗透率、核磁共振、岩电、压汞、X衍射、铸体薄片等大量配套岩石物理实验，重点考察了地层因素与渗透率、压汞喉径均值、储层品质参数、核磁共振T2谱及孔隙度之间的实验关系；在此基础上，给出两种能够简单模拟实际情况的岩石孔隙模型，首先用欧姆定律及毛管渗流原理对它们的渗透性及导电能力进行计算，然后对实验结果作出进一步分析与解释.通过实验及理论两方面的综合分析，阐明了储层渗透性与其地层因素之间的关系.

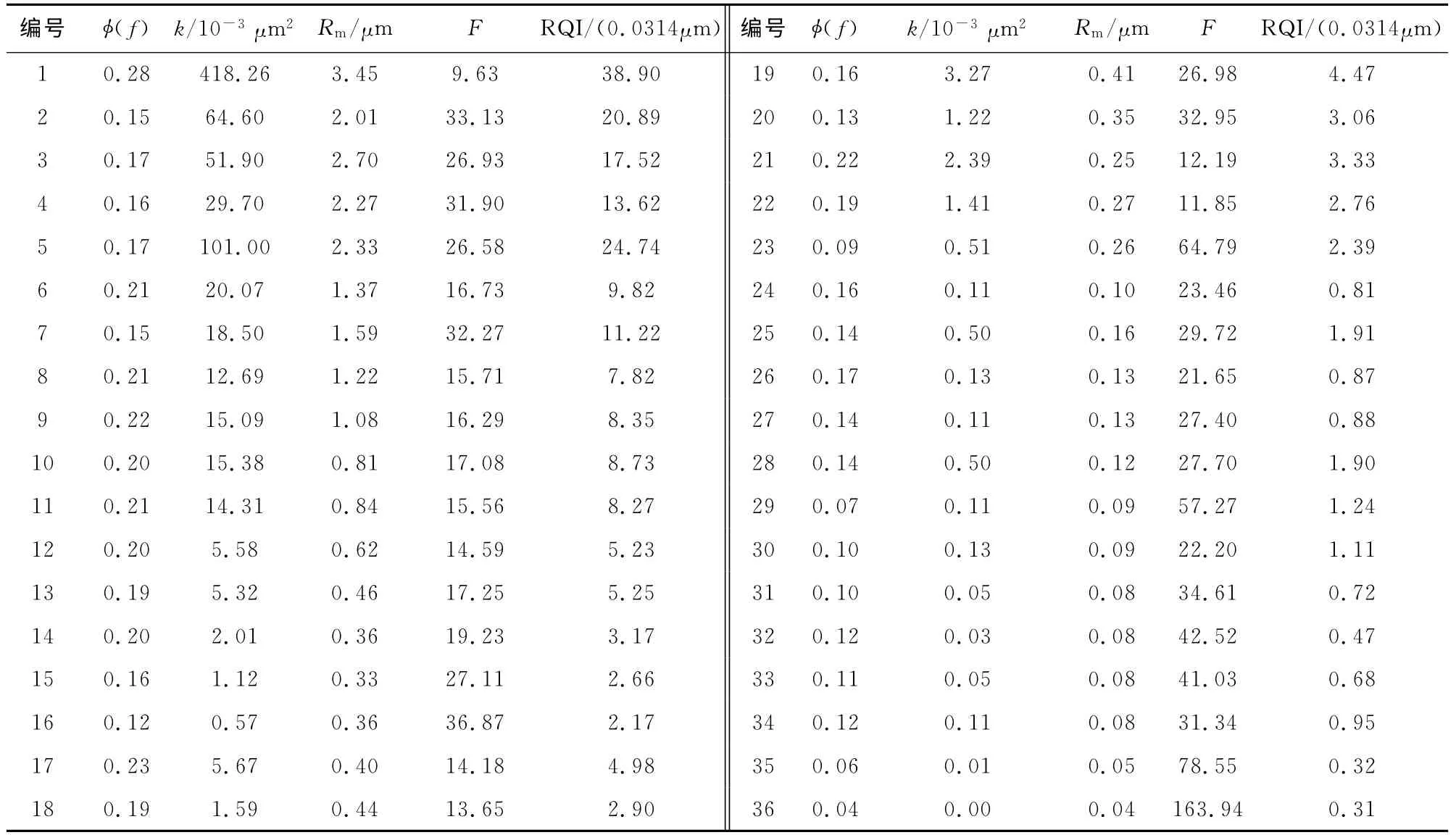
表1 岩芯样品配套的岩石物理实验数据Table 1 Experimental data of core samples

2 样品及实验结果

为了研究储层渗透性与其地层因素之间的关系，岩芯样品的选择及配套的岩石物理实验设计至关重要.因为渗透性差异直接取决于孔隙结构的差异，所以选择的岩芯样品必须能够尽可能反映不同类型的孔隙结构特征.我们首先对大量样品进行了常规孔隙度、渗透率及核磁共振等非破坏性实验测量，同时对从柱塞样得到的碎样进行X衍射和铸体薄片分析.在此基础上，根据孔、渗大小、核磁共振T2谱形态特征、矿物含量及微孔隙结构分析结果，进一步筛选了渤海湾盆地同一目标区沙河街储层的36块不同孔隙结构特征、骨架矿物不导电、没有微裂缝发育的样品进行岩电及压汞等配套岩石物理实验.

部分实验数据结果见表1.第二至六列分别为孔隙度φ（f）、渗透率k（10－3μm2）、压汞喉径均值Rm（μm）、地层因素F（无量纲）、渗透率与孔隙度的组合参数RQI（其具体含义为渗透率与孔隙度之比的平方根）.RQI一般称为储层品质指数［6－8］，表达式为：

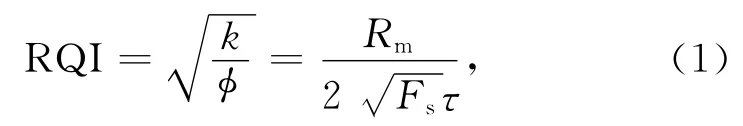
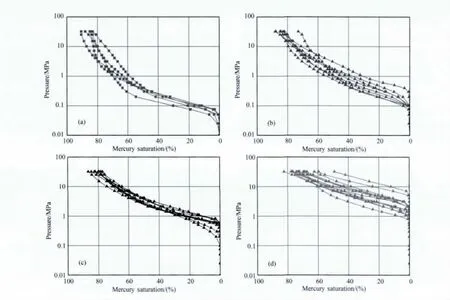
图1 全部岩芯四类孔隙结构的压汞曲线特征（a）I类压汞曲线；（b）II类压汞曲线；（c）III类压汞曲线；（d）IV类压汞曲线.Fig.1 MICP curves of all samples with four types of pore structure（a）MICP curves of I class；（b）MICP curves of II class；（c）MICP curves of III class；（d）MICP curves of IV class.

表2 四类孔隙结构的各类参数的取值分布范围Table 2 The value range of various parameters of four types of core samples

式中φ为孔隙度，小数；Fs为几何因子，无量纲；τ为喉道曲折度，无量纲.

为了便于后续分析，首先根据压汞毛管压力曲线形态及喉径均值大小将36块岩芯样品的孔隙结构分为四种类型.I类孔隙结构的样品排驱压力小于0.1MPa，平均孔喉半径的分布范围为2～3.5μm；II类孔隙结构的样品排驱压力0.1～0.5MPa，平均孔喉半径的分布范围为0.46～1.59μm；III类孔隙结构的样品排驱压力0.5～1MPa，平均孔喉半径的分布范围为0.25～0.44μm；IV类孔隙结构的样品排驱压力大于1MPa，平均孔喉半径的分布范围为0.04～0.16μm.四类孔隙结构样品的全部毛管压力曲线如图1所示，四类孔隙结构样品的喉径均值Rm、RQI等参数的分布范围详见表2.

然后，建立地层因素F－渗透率k（10－3μm2）的关系图，并与地层因素F－孔隙度φ（%）的关系图进行综合对比，如图2所示.仔细观察不难发现，地层因素相近的岩芯样品具有相近的孔隙度值，这符合阿奇公式的规律，但其渗透率的变化范围却比较大，差异明显.当孔隙度相近、渗透率仅有0.1×10－3μm2的样品与渗透率高达100×10－3μm2的样品同样可以具有非常相近的地层因素，渗透率差别高达1000倍.为了更清楚地说明这一点，我们从该图中选取了两组数据，分别显示在图3、图4中.这两组数据点对应岩芯的孔隙结构类型、地层因素F、孔隙度φ、渗透率k、喉径均值Rm、RQI及离心束缚水饱和度Swi等实验数据分别显示在表3和表4中.

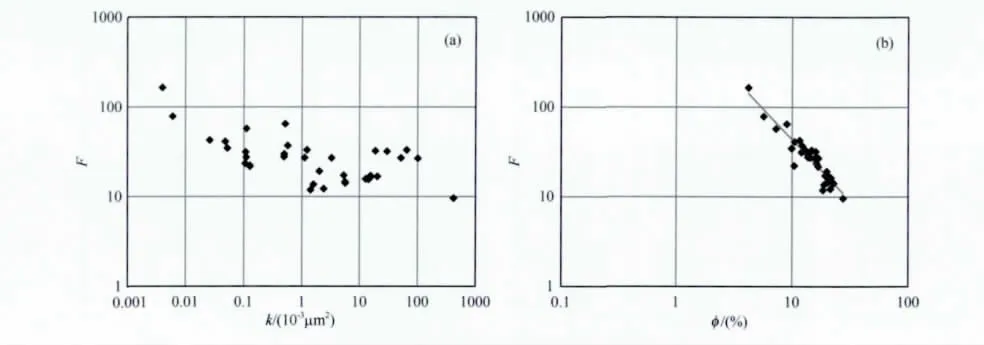
图2 全部岩芯的地层因素与渗透率、孔隙度的关系图（a）地层因素－渗透率关系图；（b）地层因素－孔隙度关系图.Fig.2 Relations of formation factor to permeability and porosity of all samples（a）Relation of formation factor to permeability；（b）Relation of formation factor to porosity.

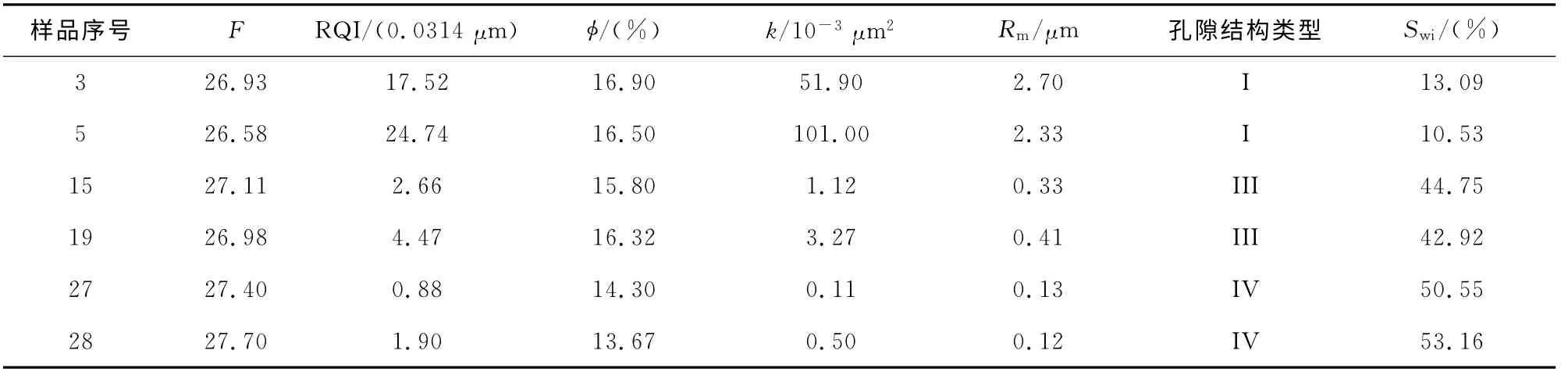
表3 从图2所选第一组岩芯的实验数据Table 3 Experimental data of the first group core samples selected from figure 2

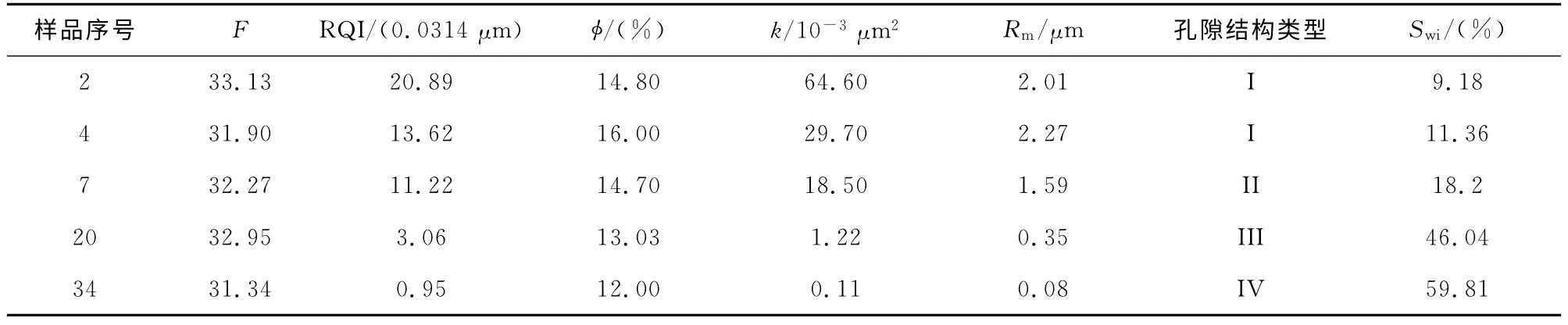
表4 从图2所选第二组岩芯的实验数据Table 4 Experimental data of the second group core samples selected from figure 2

3 实验现象分析

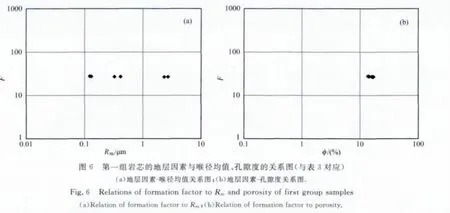
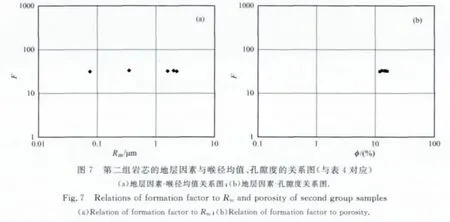
从表3、表4可以看出，孔隙度相近、渗透率差异显著的数据点，对应着不同的孔隙结构类型.因此从图2至图4中观察到的实验规律，其本质是储层微观孔隙结构与其电性响应之间的内在关系之反映.由于压汞喉径均值是直观定量衡量孔隙结构变化的参数，故将图2中的渗透率换为喉径均值，建立地层因素F－喉径均值Rm（μm）的关系图，并与地层因素F－孔隙度φ的关系图进行综合对比，考察孔隙结构与地层因素之间的内在关系，如图5所示.根据图2和图5，我们可以进一步将实验规律描述为：孔隙度相近但孔隙结构类型不同、渗透率差异明显的岩芯样品可以具有相近的地层因素值，导电能力相近.根据表3、表4，将图3、图4中的渗透率换为相应的喉径均值，如图6、7所示.

图8为表3、表4两组数据点对应岩芯的压汞曲线及核磁共振T2谱.从中可以更直观地看到，这些孔隙度相近、渗透率差异显著但地层因素相近的岩芯，其孔隙结构差异十分明显.

虽然近三十年来不断有学者注意到以束缚流体为主的微孔隙对岩石导电有影响作用，并相继提出一些导电模型来帮助理解和分析，如综合导电模型GCRMM及三水模型等［9－18］，但鲜有人直接利用实验数据来定量说明微孔隙对岩石导电能力的贡献究竟有多大.本文的研究则弥补了这一不足，通过表3—4、图3—4及图6—8所揭示的物理意义十分重要：岩石孔隙中束缚流体的导电能力不容忽视，当岩石孔隙度相近时，以微小孔隙为主、渗透率低、束缚水饱和度较高的样品可以与以大孔隙为主、渗透率高、可动水饱和度较高的样品具有相近的导电能力.表3—4、图3—4及图6—8为这一观点提供了直接的实验证据.如表3中的5号样品，孔隙度为16.5%，渗透率为101×10－3μm2，喉径均值为2.33μm，束缚水饱和度10.53%；27号样品与5号相比，孔隙度接近，但渗透率低（0.11×10－3μm2），束缚水饱和度高（50.55%），地层因素却与5号十分接近.两块岩芯的渗透率之比为909.9（5号与27号相比），束缚水饱和度之比为0.2.

我们先前的研究认为，储层品质指数RQI能够很好地反映储层孔隙结构特征［19－20］.从表2也不难看出，根据压汞数据对孔隙结构的分类结果，不同类型的RQI分布范围没有任何重叠，说明如果单独采用RQI对储层孔隙结构进行分类，能够达到与压汞数据相同的结果.将图5中的喉径均值换为RQI图中，更方便我们观察实验规律.此外RQI参数还有一个重要优点，就是它在实验室测量中非常易于获得，成本低廉，在知道孔隙度和渗透率后，就可以计算得到.在研究储层渗透性或孔隙结构与电性响应的内在关系方面，地层因素－RQI关系图非常简单实用.

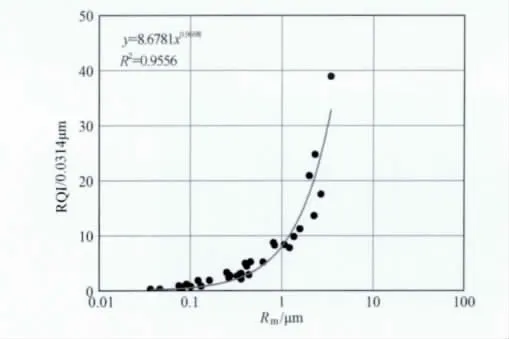
图10 全部岩芯的储层品质指数与压汞喉径均值的关系图Fig.10 Relation of RQI to Rmof all samples

4 理论探讨

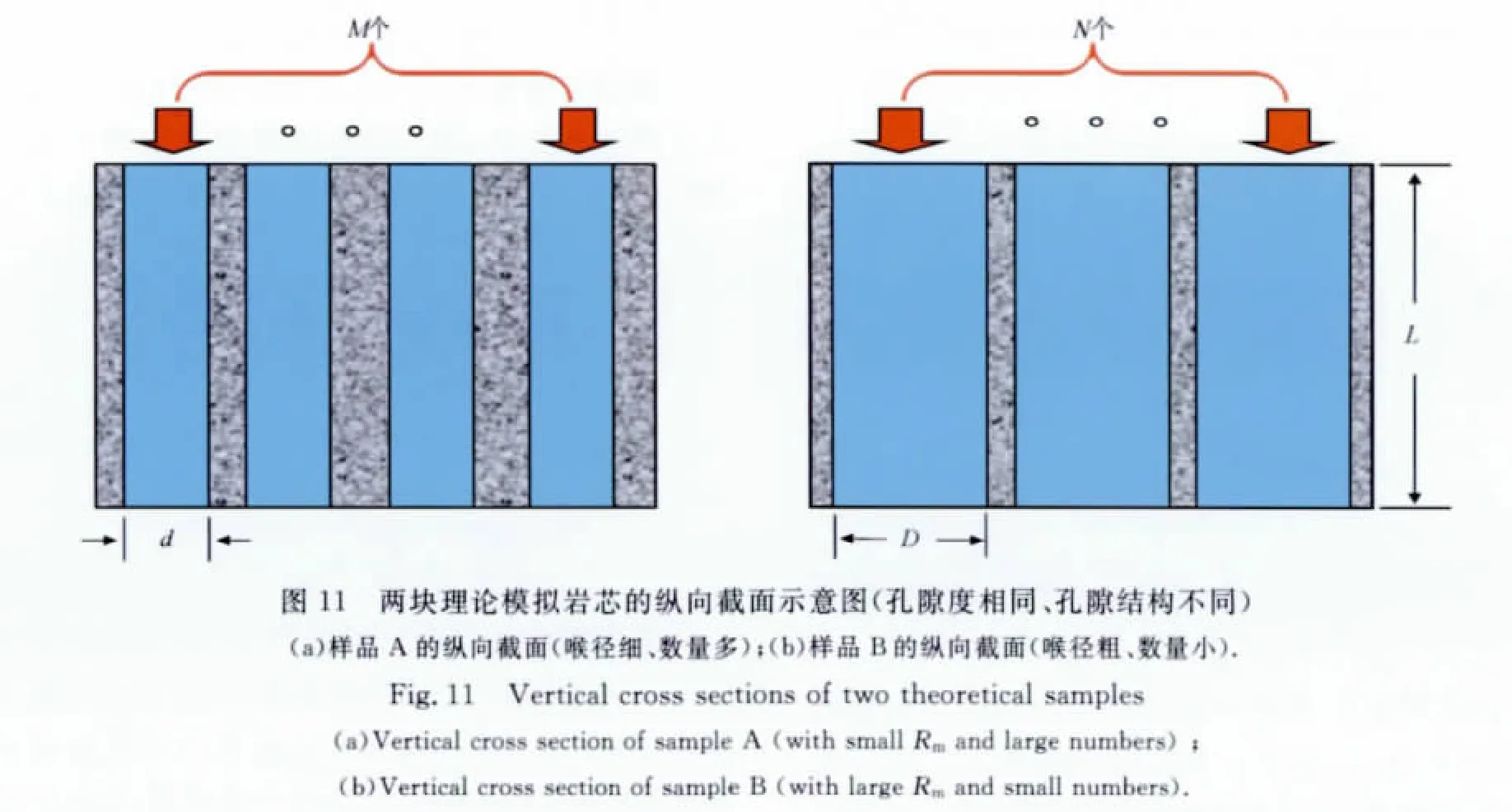
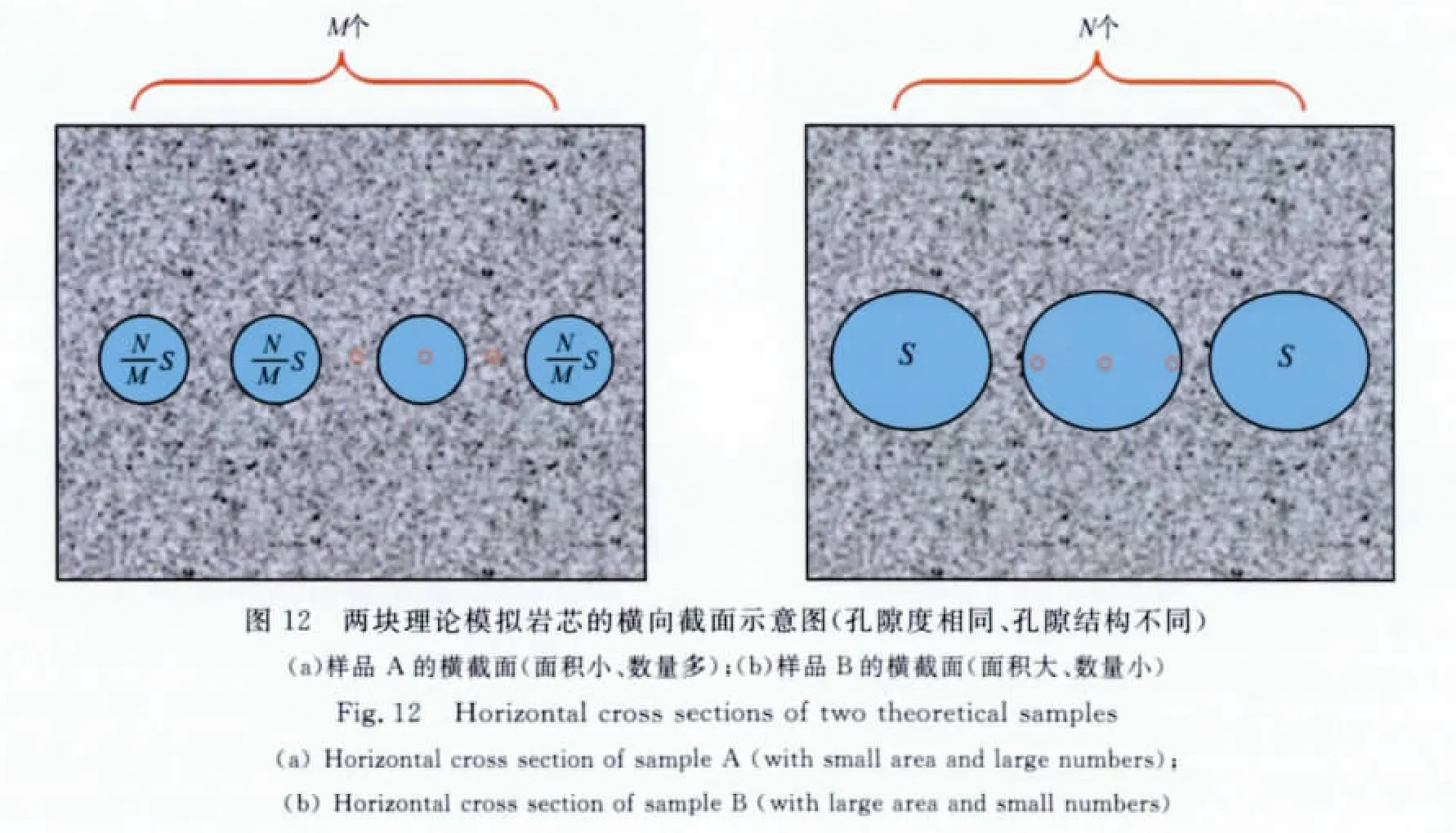
配套的岩石物理实验及综合对比分析表明，孔隙度相近但孔隙结构类型不同、渗透率和束缚水饱和度差异明显的岩芯样品可以具有相近的导电能力.如何从理论分析的角度更深刻地理解这一重要的实验现象呢？地层因素与压汞喉径均值的交绘图（见图5）提示我们，孔隙结构的差异可以用毛管半径的大小来反映，故可对孔隙度相近但孔隙结构类型不同的岩芯样品进行如下的地质模型抽象：假设有两块碎屑岩岩芯，二者具有相同的几何形状、体积及孔隙度，它们的孔隙空间均由毛细管组成，均饱和相同性质的流体.样品A由较多的直径较细的毛管组成，数量设为M个，每个毛管的直径为d，底面圆形面积为SA；样品B由较少的直径较粗的毛管组成，数量设为N个，直径为D，底面圆形面积为SB；两块样品的毛管长度均为L.其纵向截面的具体示意图如图11所示.图中箭头代表流体流动及电流运动方向.两块样品的水平向截面示意图如图12所示.因此两块样品具有相同的孔隙度和曲折度，不同之处在于它们的孔隙结构特征，即样品A模拟由许多数量的小孔隙组成的孔隙系统，样品B模拟由少量大孔隙组成的孔隙系统.由于两块样品的体积及孔隙度相同，且毛管长度也相同，所以有如下关系：

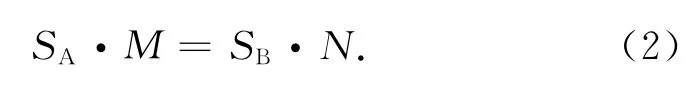
根据前述假设，SA＜SB，M＞N.样品A、B的电阻分别表示为RA和RB，各自每个毛管的电阻分别表示为PA和PB.则根据并联导电原理及公式（2），二者的电阻之比为：

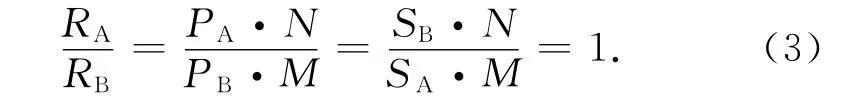
样品A、B的渗透率分别表示为kA和kB，因为二者具有相同的孔隙度、曲折度及几何形态，故根据公式（1），二者的渗透率之比为：

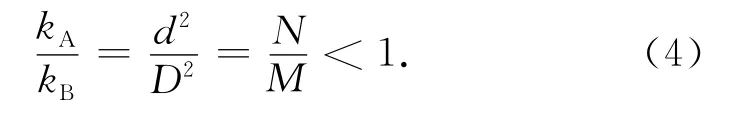
上述简单的理论分析说明，孔隙度相近但孔隙结构不同的样品，它们的渗透率不同，但导电能力却可以非常接近，这一理论分析结果与实验观察到的规律相吻合.根本原因在于流体在孔隙介质中的渗流过程与离子在其中的导电过程有着本质区别.在孔隙度相近时，流体渗流能力受控于岩石喉径均值大小，随着喉径均值的减小而显著降低（公式（1）、公式（4））；而离子在孔隙介质中的导电能力则主要受控于连通的孔隙空间大小（公式（3））.

理论分析还说明，在孔隙度、孔隙曲折度及几何形态均相近时，岩芯渗透率的差异与各自喉径均值的平方比密切相关.如表4中的2号、34号样品，它们的孔隙度相近（二者比值为1.2）、孔隙结构及渗透率的差异均十分明显（喉径均值的平方比为631.3，渗透率之比为587.3），地层因素却十分接近（地层因素之比为1.1）.该实例中，喉径均值平方比与渗透率之比十分接近（前者与后者之比为1.1），与公式（4）的结论基本吻合.需要说明的是，实际样品的孔隙结构远比我们抽象的假设条件复杂，根据公式（1），在孔隙度相近时，不同样品的渗透率比值除与喉径均值的平方比相关外，还受孔隙几何形状、孔隙曲折度等因素影响.因此孔隙度相近、孔隙结构或渗透率不同、地层因素相近的岩芯样品，它们的渗透率之比与喉径均值之比并不总是十分接近.如表3中的5号、27号样品，它们的孔隙度之比为1.2，喉径均值的平方比为321.2，渗透率之比为918.2，地层因素之比为0.97.该例中，喉径均值平方比是渗透率之比的0.35倍，表明两块岩芯样品的孔隙几何形态及曲折度有明显差异.

5 认识与结论

（1）储层品质参数与压汞喉径均值呈幂函数关系，二者之间具有非常好的相关性.在成本、时间受限的情况下，可以用该参数替代压汞参数来反映孔隙结构特征，进而借助该参数进行与孔隙结构有关的岩石物理实验规律分析.

（2）储层渗透性与其地层因素之间的关系主要表现在：①孔隙度相近但孔隙结构类型不同、渗透率差异明显的岩芯样品可以具有相近的导电能力，从本文实验数据看，具有此种规律的样品的渗透率差异可高达数百倍，这种差异与喉径均值的平方比、孔隙曲折度及几何形态相关；②从本文建立的地层因素－渗透率关系图可以看到，当渗透率大于100×10－3μm2时，地层因素随着渗透率的增加有迅速减小趋势；当渗透率小于0.01×10－3μm2、孔隙度小于5.7%时，地层因素随着渗透率的减小有迅速增加趋势.这在一定程度上反映了两种极端情况，一种是储集空间和渗透性趋于极差的情况，一种是趋于极好的情况，对应的导电能力也分别趋于极差和极好.

（3）根据结论（2）不难看出，储层渗透性与其导电能力之间并非简单的单调函数关系，“岩石渗透性越差、其导电能力越差，渗透性越好、导电能力越好”这一观点并不正确.对于孔隙度相近、渗透率在（0.01～100）×10－3μm2这一区间变化的岩芯样品，可以具有相近的地层因素.这一重要认识对于正确理解低渗透致密储层的导电能力、提高利用电阻率测井资料识别评价低渗透油气藏精度具有重要的理论研究价值及现实意义.

（

）

［1］ Archie G E.The electrical resistivity log as an aid in determining some reservoir characteristics.AIME，1942，146（1）：54－62.

［2］ Winsauer W O，Shearin H M Jr，Masson P H，et al.Resistivity of brine－saturated sands in relation to pore geometry.Bull.Amer.Assoc.Petr.Geols.，1952，36：253－277.

［3］ Alger R P.Interpretation of electric logs in fresh water wells in unconsolidated formations.SPWLA 7thAnn.Logging Symp，1966.

［4］ Carothers J E.A statistical study of the formation factor relation.TheLogAnalyst，1968，9（5）：13－20.

［5］ Ogbe D，Bassiouni Z.Estimation of aquifer permeabilities from electric well logs.TheLogAnalyst，1978，19（5）：21－27.

［6］ Amaefule J O，Mehmet A，Laboratories C，et al.Enhanced reservoir description：Using core and log data to identify hydraulic（flow）units and predict permeability in uncored intervals／wells.68thAnnual Technical Conference and Exhibition of the Society of Petroleum Engineers，1993，SPE 26436：205－220.

［7］ Kozeny J.Uber Kapillare Leitung des Wassers im Boden，Sitzungsberichte.Royal Academy of Science，Vienna，Proc.ClassI，1927，136：271－306.

［8］ Carmen P C.Fluid Flow through Granular Beds.AIChe，1937，15：150－166.

［9］ Diederix K M.Anomalous relationships between resistivity index and water saturation in the rotliegend sandstone.SPWLA 23rdAnnual Logging Symposium，1982.

［10］ Swanson B F.Microporosity in reservoir rocks－its measurement and influence on electrical resistivity.SPWLA 26thAnnual Logging Symposium，1985.

［11］ Givens W W.Formation factor，resistivity index，and related equations based upon A conductive rock matrix model（CRMM）.SPWLA 27thAnnual Logging Symposium，1986.［12］ Givens W W.A generic electrical conduction model for lowcontrast resistivity sandstones.SPWLA 29thAnnual Logging Symposium，1988.

［13］ Crane S D.Impacts of microporosity，rough pore surfaces，and conductive minerals on saturation calculations from electric measuremens：An extended Archie′s“Law”.SPWLA31stAnnual Logging Symposium，1990.

［14］ 曾文冲.油气藏储集层的测井评价技术.北京：石油工业出版社，1992.

Zeng W C.Well Logging Evaluation Technologies of Oil and Gas Reservoirs（in Chinese）.Beijing：Petroleum Industry Press，1992.

［15］ 莫修文，李舟波，贺铎华等.三水导电模型及其在低阻储层解释中的应用.长春科技大学学报，2001，3（1）：92－95.

Mo X W，Li Z B，He D H，et al.The application of threewater conduction model in the interpretation of low－resistivity reservoir.JournalofChangchunUniversityofScienceand Technology（in Chinese），2001，3（1）：92－95.

［16］ 李舟波，莫修文，王谦等.塔里木盆地低阻泥质砂岩油气储层导电模型的建立和应用.“九五”全国地质科技重要成果论文集，2000.

Li Z B，Mo X W，Wang Q，et al.The electrical conductivity model and its′applications in shale sands of Tarim Basin with low resistivity（in Chinese）.Proceedings of National Geology Science and Technology Achievements in the Ninth Five Years Plan.2000.

［17］ 闫磊，潘保芝，莫修文等.几种评价低阻储层的导电模型.吉林大学学报（地球科学版），2007，37（S1）：121－125.

Yan L，Pan B Z，Mo X W，et al.Study on some low resistivity reservoir models.JournalofJilinUniversity（EarthScienceEdition）（in Chinese），2007，37（S1）：121－125.

［18］ 张丽华，潘保芝，李舟波等.新三水导电模型及其在低孔低渗储层评价中的应用.石油地球物理勘探，2010，45（3）：431－435.

Zhang L H，Pan B Z，Li Z B，et al.New three－water conduction model and its application in evaluation of low porosity and low permeability reservoir.OilGeophysical Prospecting（in Chinese），2010，45（3）：431－435.

［19］ 刘忠华.储层孔隙结构的测井评价方法研究［硕士论文］.北京：中国石油勘探开发研究院，2003：14－24.

Liu Z H.Research on well logging evaluation method of formation pore structure［Master′s Thesis］（in Chinese）.Beijing：Research Institute of Petroleum Exploration and Development，2003：14－24.

［20］ 张龙海，周灿灿，刘国强等.孔隙结构对低孔低渗储集层电性及测井解释评价的影响.石油勘探与开发，2006，33（6）：671－676.

Zhang L H，Zhou C C，Liu G Q，et al.Influence of pore structures on electric properties and well logging evaluation in low porosity and permeability reservoirs.PetroleumExploration andDevelopment（in Chinese），2006，33（6）：671－676.