电厂热工智能控制系统的研究

崔师明，范山东

(1.黑龙江林业高级技术学院，黑龙江 绥化 152061;2.黑龙江科技学院电气与信息工程学院，黑龙江 哈尔滨 150027)

0 前言

电厂热工是一个大滞后、非线性、时变的控制过程。为了在工业中更好的控制纯滞后时变系统，不少学者基于内模控制结构，综合各种控制(如模糊控制、自适应控制、神经网络)的优点，提出了很多控制方法。而本文首先在总结2 自由度内模控制的调节方法和规律的基础上，采用模型参考自适应控制的思想，将模糊控制方法和内模控制方法结合在一起，提出了一种模型参考模糊自适应内模控制方法:采用相消法设计内模控制器，用参考模型理想输出和实际对象输出之差e 及其变化率Δe 在线模糊调节控制器中滤波参数，目标是使系统输出平稳快速［1］。仿真结果表明，这种方法可以使系统的性能达到快速性和鲁棒性的最佳结合。然后，在总结前人对输入受限问题的处理经验的前提下，提出了一种限幅状态与内模控制相互切换的方法。最后，把控制器滤波参数的模糊自整定和有输出限幅的内模控制二者有机的结合起来，发挥各自的长处，形成在线智能切换的模型参考自适应内模控制方法，对由国内某500 MW 火电厂锅炉一级减温系统的实际阶跃响应信号拟和出来的相应的一级减温被控对象动态传递函数进行仿真，并与常规内模控制系统、PID 控制系统作各种性能比较［2］。仿真结果表明，采用本文提出的方法在系统响应的快速性、鲁棒性和抗干扰方面都得到了较大改善，从而证明了方法的正确性和有效性。

本文综合应用内模控制方法和模型参考自适应控制的思路，控制器的设计用内模结构的相消法设计，调节信号来自参考模型输出与系统实际输出的误差及其变化率，采用模糊调节，目标是使系统输出平稳快速［3］。系统结构如图1 所示。

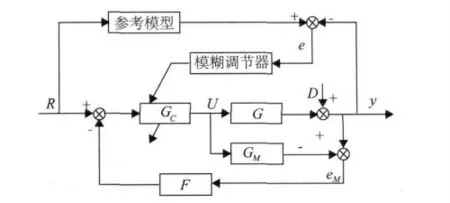
图1 系统示意图

1 控制量限幅的内模控制器

工业过程控制中，大部分控制量由于执行机构等的限制，控制信号的幅度和变化率都受到限制，若直接应用未考虑控制受限的控制器就相当于在系统中引入了非线性环节，性能将大幅度下降。为了解决该问题，在总结前人对输入受限问题的处理经验的前提下，提出了一种限幅状态与内模控制其相互切换的方法，即根据系统响应是否在误差带范围内及系统的模型预测输出是否超过一该误差带，来共同确定控制量在限幅值与内模控制器输出值之间进行在线智能切换［4］。采用智能控制器的系统结构图如图2 所示。

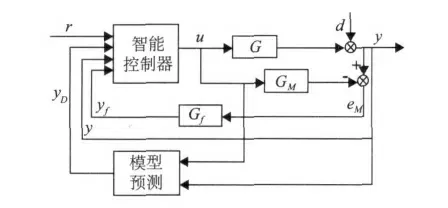
图2 智能内模控制结构图

如图3，设y1和y2分别为系统实际响应误差带的下、上限，y1'和y2'分别为系统预测输出的上、下限，y1，y2，y1'，y2'均可在线调整;yp(k+L)为系统模型预测输出值，其L 表示滞后步数。为严格限制控制量u，保证系统良好的响应速度及抗扰性，且系统响应不出现过大超调，对控制器的输出采用分段计算的方法。即当系统响应小于y1且模型预测值也小于y1'时，用最大限幅值，以提高快速性;y(k)＜y1且yp(k+L)＜y1'，按最大限幅值计算u(k);当系统响应大于y2且模型预测值也大于预测误差带y2'时，用最小限幅值;y(k)＞y2且y(k +L)＞y2'，按最小限幅值计算u(k);其余时候就直接按式y=Gr×r +Gd×d=r计算控制量u(k)(图3)。

图3 误差带示例

为验证本方案的有效性，将本文方案与直接用常规内模控制器输出加限幅相比。取常见的一阶惯性对象加纯滞后，即实际对象为:

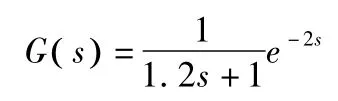
采样周期T=1 s，加零阶保持器后离散化模型为:

控制量限幅值为0≤u(k)≤1.8，取α=0.4，β=0.7，参考信号r 为单位阶跃信号，在仿真时间40 s 时加一幅值为0.5 的阶跃扰动。

当模型精确时，智能控制系统对应参数为:y1=0.85，y2=1.1，y1'=1，y2'=0.88，响应如图4 中实线所示，直接用常规内模控制器输出加限幅时，系统响如图4 中虚线所示。控制量均经系数为0.3 的变换后，表示在图下方。

图4 模型精确时的系统响应

当对象参数发生20%变化时，即实际对象为

本智能控制系统对应参数为:y1=0.8，y1'=0.95，y2=1.15，y2'=0.9.响应如图5 中实线所示;直接用常规内模控制器输出加限幅时，系统响应如图5 中虚线所示。控制量均经系数为0.3 的变换后，表示在图下方。以上仿真结果表明，本文方案在其响应速度、抗扰性及鲁棒性等方面都有一定改善。

图5 模型失配时的系统响应

2 模型预测的改进

考虑到实际对象中存在着时变或非线性等因素，或多或少的存在模型误差，加上系统中的各种随机干扰，使得预测模型不可能于实际对象的输出完全一致。上一节所述方法的不足之处是，因为预测是基于模型，当模型失配越大，预测就越不准确，从而影响控制效果［5］。现举例如下:

假定对象模型为:

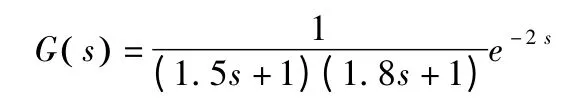
采样时间T=1 s，则其加零阶保持器的离散化模型为:

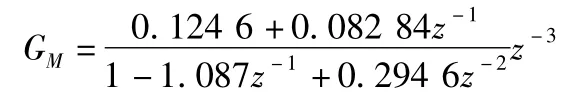
当实际对象有模型失配时，实际对象变成了:

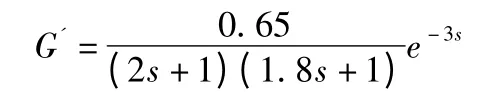
这时，对于单位阶跃输入，在T=40 s 时加一幅值为0.5 的阶跃扰动，根据模型的预测结果如图6 中点划线所示。

图6 模型失配时的系统预测和真实响应图

图6 中实线为实际输出。从图6 可以很清楚的看出，由于模型的失配，使得预测效果完全偏离系统的真实输出。上述的预测都是完全基于其模型，实质上是开环的。在预测控制中，其最具生命力的三大特征之一便是反馈校正。借鉴其思路，也利用反馈校正来修正开环模型预测。具体的做法就是:将第k 步的实际对象输出测量值y(k)与预测模型输出ym(k)之间的误差，加到模型的预测输出ym(k+i)上，得到闭环输出预测，用yp(k+i)表示:

其中:h 为修正误差系数，em(k)为k 时刻预测模型输出误差。

由于系统存在纯时延t，最开始em(k)(k=l，2，…，t+l)是0，到了t+l 时刻就会在预测值上突加一个em，对预测值有一定振荡，为了减小这个影响，本文对h 取变参数，刚开始时取h＜l，慢慢增加h，最终取h=1。上述模型失配系统的预测结果如图7 点划线所示。实线为实际输出。图7 改进后的预测输出图。根据上述改进预测输出的思想，对上面的系统进行仿真。系统对象为:

图7 改进后的预测输出图

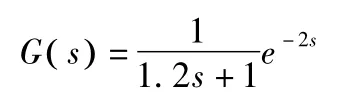
而发生模型失配后，实际对象为:

仿真结果如图8 中实线所示，点划线为未加改进的模型预测所得响应曲线。控制量均经系数为0.3 的变换后，表示在图下方。由图8 和图5 可以看出，利用改进后的带反馈校正的模型预测代替简单模型预测作为系统预测输出，系统响应比改进前有更好的响应特性，从而验证了本文方法的正确性和有效性［6］。

图8 改进后有模型失配时的系统响应图

3 仿真研究

在前面的章节里已经分别讨论了控制器滤波参数的模糊自整定和有输出限幅的内模控制问题，且分别作的仿真都己经证明了方法的正确性和有效性。本文把二者有机的结合起来，发挥各自的长处，形成在线智能切换的模型参考模糊自适应内模控制方法。结构框图如图9。

图9 采用模糊调节器的自适应内模控制

为了验证本文提出的该方法的有效性，用Matlab 对系统进行仿真，仿真框图采用图9 的结构，并将系统仿真结果与模型参考模糊自适应内模控制加限幅输出方法进行比较。上图中，G 为实际对象，GM为被控对象模型，Q是包含调节滤波参数和处理有控制限幅的智能控制器，F馈为反滤波器，R，D 和Y 分别代表参考输入、扰动和输出，M，e，e 和Δe 分别表示模型误差、理想输出和实际输出之差e 及其变化率［7］。

对象模型为工业过程中常见的二阶惯性环节加纯滞后

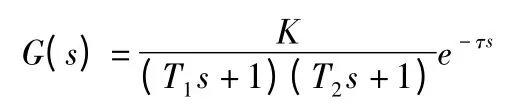
其中，T1=1.5，T2=1.8，K=1，τ=2 采样周期为T=1 s，则其加零阶保持器的离散化模型为:

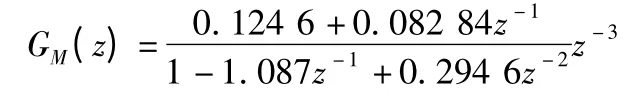
被控对象分别取以下3 种形式(采样周期T=0.5 s):

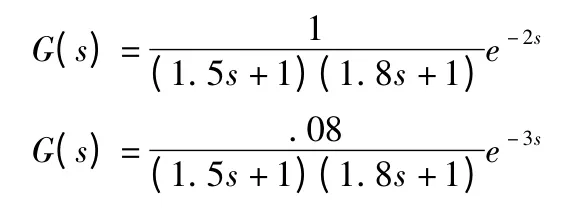
从仿真结果可以看出，无论有无模型误差，采用本文提出的方法在系统响应的快速性、平稳性和鲁棒性方面都得到了较大改善，从而证明了本文方法的正确性和有效性。

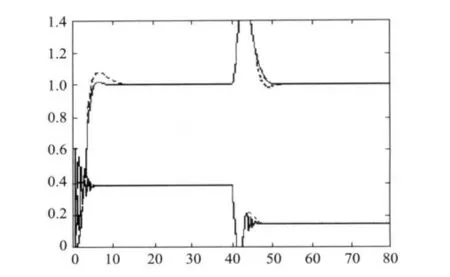
图12 系统(3)的响应曲线

4 结论

在结合对输入受限问题的处理经验的前提下，本文根据系统响应是否在误差带范围内及系统模型的预测输出是否超过该误差带，来共同确定控制量在限幅值与内模控制器输出值之间进行在线智能切换。其特点是:在线调节时，当滞后增大或者模型失配时，适当减小系统实际响应误差带和系统预测输出的的上限，增大系统实际响应误差带和系统预测输出的的下限，便可获得较好的效果，该方法简单实用，便于在线调节，具有一定的工程应用价值;另外，对模型失配较大情况下预测不准进行了讨论，受预测控制的启发，在模型预测中引入反馈校正，即根据k 时刻以及以前时刻的预测误差对未来的模型预测值进行修正。使预测更加准确，从而更精确的决定控制状态的切换和控制量的选取，使系统响应获得更好的快速性、平稳性和抗扰性。仿真结果证明了本文方法的正确性和有效性。

［1］张玉铎，王满稼.热工自动控制系统［M］.北京:水利电力出版社，1984.

［2］Garcia C.E.，Morari，M.Intemal model control.2.Design procedure for multivariable systems.I＆EC process Des.Dev.，1985，24(2):472-484.

［3］祝小莲，等.一种有输出限幅的智能内模控制器设计方法［J］.昆明理工大学学报.2001，26(增刊):132-134.

［4］郭巨众.模糊内模控制模糊内模控制及其在过热汽温控制中的应用［M］.太原:太原理工大学，2003.

［5］李成鑫，赵耀.有控制输出限幅的智能内模控制器的一种改进［J］.贵州科学学报，2002，20(4):10-12.

［6］廖明，吴宁，谢品芳.神经网络内模控制算法的研究［J］.电气传动自动化，1998，20(4):24-28.

［7］范影乐，杨胜天，李轶.MATLAB 仿真应用详解［M］.北京:人民邮电出版社，2001.