一类求解广义特征值问题的瀑布型多重网格法
白建军,胡 晔 (吕梁学院数学系,山西 吕梁033000)
笔者研究满足Lipschiz条件的常系数连续电磁场Maxwell方程组[1],即求向量场u满足:

式中,Ω∈R2为连通多项式域,∂Ω表示Ω∈R2的边界;n表示∂Ω的外法向单位向量。通过有限元离散,最终将式 (1)中特征值的计算转化为求解线性方程组的问题,对于大型矩阵计算问题,笔者以并行保域逆迭代法为光滑子,结合新外推方法提出一类求解广义特征值的方法。
1 有限元离散
为了离散式 (1),先将区域Ω作三角剖分。根据变分原理[2-5],由有限元逼近[4]将问题转化为:
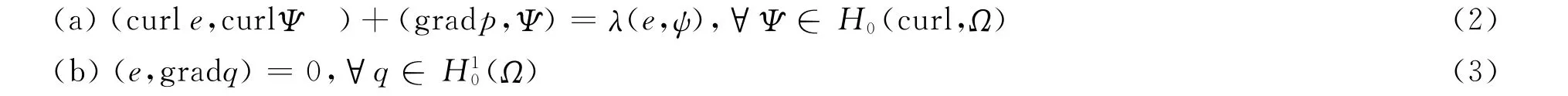
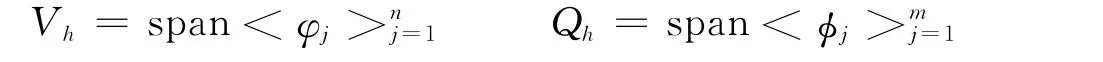
定义:
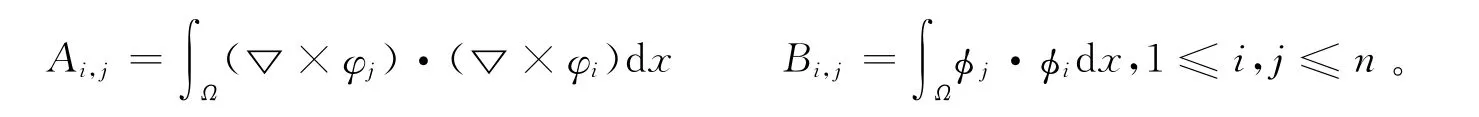
则式 (2)和式 (3)可导成A X=λB X形式。其中,A和B都是n×n实矩阵。
2 光滑过程并行保域逆迭代算法 (PDS)
周树荃[6-7]等提出并行保域逆迭代算法有效避免了漏根、迭代过程的不收敛等缺点,提高了解的精度。
算法1(对称不定矩阵LDLT分解在标准存储格式下的并行计算) 由于矩阵A∈Rn×n具有对称性,利用该算法求单位三角矩阵L=(lij)和对角方阵D,使A=LDLT成立。当i>j时,lij将元素Aij覆盖;当i=j时,di将元素Aij覆盖。
步5 k←k+1,如果k>n,停止;如果k≤n,执行步2。
步4 利用Rayleigh商处理近似的特征值,使其尽量精确化
步8 控制迭代,设kk为任意大于零的整数 (一般设置为6)如果k≤kk,执行步2;若不满足k≤kk,执行以下步骤。
3 瀑布型多重网格法 (NCGMGE)
文献 [8]只能对u进行更新,而不能更新λ。而以特征值共轭梯度法[9]为基础的特征值瀑布型多重网格方法 (NCGMGE)[10],在循环迭代过程中,能使 (λ,u)中的λ和u同时得到更新。具体算法如下:

end
4 新的瀑布型多重网格算法 (WPECMG)
为了提高运算的收敛速度,文献 [11]提出并改进了外推方法,笔者结合新外推方法,以PDS法为光滑子给出求解特征值问题一类新的瀑布型多重网格算法 (WPECMG)。具体算法如下:的精确解
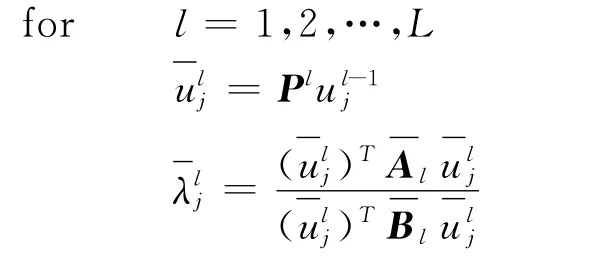
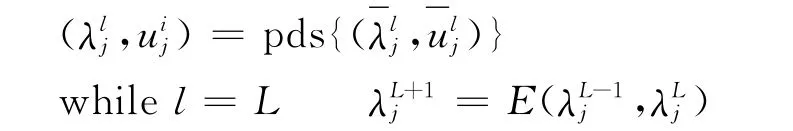
end
根据文献 [12]可以得到,在有限元进行离散以后,对于模小的特征值可以得到逼近程度较好的解。
5 数值试验
考虑模型如 (1)所示,仅考虑二维平面下的方程,求解区域为Ω=[0,a]×[0,b],方程组的真解为:

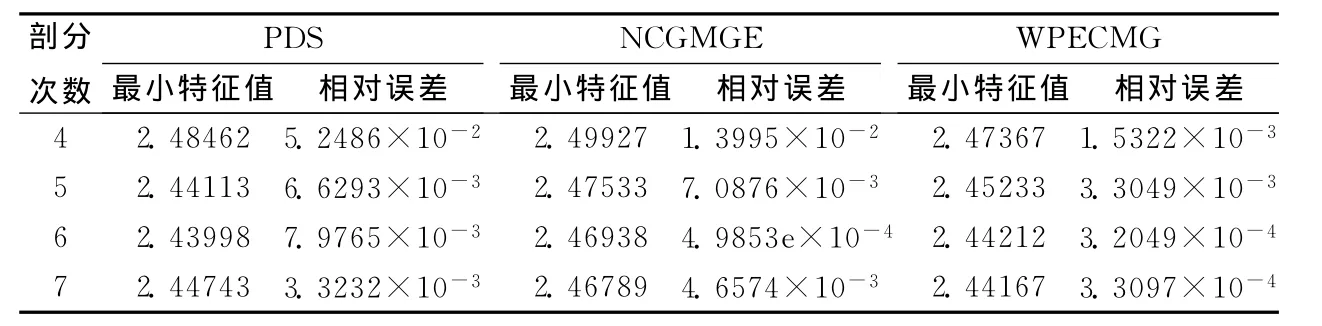
表1 PDS、NCGMGE与WPECMG的数值结果

表2 PDS、NCGMGE与WPECMG的时间结果
[1]Arbenz P,Geus R.Solving Maxwell eigenvalue problems for accelerating cavities [J].Phys Review ST Accel Beams,2001 (4):20-23.
[2]王生楠 .有限元素法中的变分原理基础 [M].西安:西北工业大学出版社,2005.
[3]林金木 .有限单元法变分原理与应用 [M].长沙:湖南大学出版社,2003.
[4]Hiptmair R.Canonical construction of finite element[J].Math Comput,1999,68 (5):1325-1346.
[5]Watanabe K,Igarashi H.Robustness of nested multigrid method for edge-based finite elem-Ent analysis [J].IEEE Transactions on Magnetics,2009,45 (3):1088-1091.
[6]周树荃,曾岚 .求解广义特征值问题的并行保域行列式查找法 [J].南京航空航天大学学报,1995,27(2):148-154.
[7]周树荃,戴华 .求解对称带状矩阵广义特征值问题的保域行列式查找法 [J].南京航空学院学报,1985,17(4):23-30.
[8]Chen C M,Hu H T,Xie Z Q,et al.Analsis of extrapolation cascadic multigrid method [J].Science in china Series A:mathematics,2008,51 (8):1349-1360.
[9]刘寒兵 .一种有效的广义特征值分析方法 [J].固体力学学报,2003,24(4):419-426.
[10]匡前义,李郴良,李明 .一种求解广义特征值的瀑布型多重网格方法 [J].云南民族大学学报,2009,18(3):202-205.
[11]Chen C M,Xie Z Q,Li C L,et al.Study of A New Extrapolation Multigrid Method[J].湖南师范大学自然科学学报,2007,30(2):1-5.
[12]Weiss B,Biro O.Edge element multigrid solution of nonlinear magnetostatic problems [J].Comple,2001,20 (2):357-365.

