液体静压导轨的仿真和实验模态分析
郝 乐,刘一磊,郝 瑾,马 波,成法坤,汪 洋
(1.中国重型机械研究院股份公司,陕西 西安 710032;2.哈尔滨工业大学,黑龙江 哈尔滨 150001)
0 前言
超精密机床的加工性能与动态特性有密切关系,尤其在工作时产生的振动不仅会影响机床动态精度和工件的表面质量,而且还会降低生产效率和刀具耐用度,甚至会降低机床的使用寿命,同时产生的噪声对环境有严重影响,因此超精密机床的动态性能成为了研究热点之一[1-3]。在超精密机床中,为实现高刚度和大承载力,液体静压导轨被广泛采用。设计静压支承时,在考虑静态性能的同时还应根据工作情况兼顾动态性能,特殊情况下动态性能可能成为主要矛盾,并直接关系到整个机床的性能,所以对液体静压导轨进行动态分析十分必要,而模态分析是动态分析的重要部分。此外在超精密机床的液体静压导轨中,由于各个零件的机加工和部件的组装中存在误差,同时导轨结构在油膜压力下发生变形,使得导轨的实际参数与设计值间存在偏差。虽然液压油膜能够均化误差,减小了设计值与实际参数的差异;但由于超精密机床的高性能要求,仍需要更准确地确定机床导轨的模态参数,以掌握超导轨的性能。
华中科技大学的陈学东等人对所研制的超精密定位工作台导轨的动态性能进行深入的研究,不仅得到了性能优良的工作台,更为机床导轨动态性能的研究提供了好的方法[4]。本文对设计的液体静压导轨进行了仿真和实验模态分析,得到了液体静压导轨的固有频率和模态阵型,并对油膜结合面的阻尼系数进行识别,以更好的确定结构导轨的动态特性。
1 液体静压导轨的仿真模态分析
在液体静压导轨设计完成后,对其进行仿真模态分析是非常必要的,这可以对结构的合理性进行分析,并预测该结构的固有频率和模态阵型。本文的液体静压导轨采用了通用的结构形式,如图1 所示,主要由滑台,幅板和“T”型支承组成。对其进行有限元建模,如图2 所示,采用弹簧单元(COMBIN14)来实现导轨结合面间的刚度,不设置阻尼系数;在实际结构中,导轨幅板之间,幅板与滑台之间是用螺钉固定在一起,但由于模态分析时不能含有非线性因素,因此对导轨幅板之间以及幅板和滑台之间进行了粘接处理,这会给仿真结果带来不可避免的误差。


在有限元模型中,由于静压导轨的滑台受到直线电机驱动,因此在滑台Z 轴方向施加约束;此外“T”型支承与大理石基座相连,对支承底面施加“零位移”的全约束。通过对有限元模型进行有重力的预应力模态计算后,得到了固有频率和模态振型。图3 a~d为静压导轨的前4 阶振型。从中可以看出一阶固有频率为59.19Hz。

2 液体静压导轨的实验模态分析
为准确掌握液体静压导轨的动态特性,得液体静压导轨的实际模态参数,并对前面有限元结果进行验证,判断预测方法的可行性和结果的准确性,对液体静压导轨进行实验模态分析是非常重要的。油膜动态特性实验方法有两大类:时域法、频域法。针对本文设计的液体静压导轨实际结构和现有实验设备,采用了锤击方式的频域分析法。锤击法是一种宽频激励的方法,一次锤击产生的绕动力包含了宽频范围内各种频率的信号,此外力锤激励对结构无附加质量,不会对结构的动态特性产生影响,实验效率高,设备少且相对简单,实验周期较短。锤击激励法比较适合于零件、部件、轻型、小型机械结构的激振试验[5]。
此外,实验采用固定激励,逐点拾振的方法进行传递函数的测量。实验中,锤击法实验模态分析的主要组成如图4 所示,设备由激励器(PCB PIEZOTRONICS 公司的086c03 型力锤,其上附加有力传感器)、加速度传感器(PCB PIEZOTRONICS 公司的M353B18 型)和动态信号分析仪(Agilent 35670A)等设备组成。

图4 实验系统组成Fig.4 Composition of experimental system
通过上述实验得到了频率响应谱图及对应的相干函数。实验中,拾阵点位于滑台和幅板表面的油腔位置,激励点位于滑台和幅板的中心位置,如图5 所示。此外采用了在同一点多次触发,取平均值的方法计算最终的频响函数。但是由于人为因素,锤击点的位置不能保证完全相同,这对测量结果会存在着一定的影响。图6为激振力函数,呈现明显的尖脉冲形式,证明了输入信号的有效性。取在7 点激励在4 点拾振所测量得到的频响函数和相干函数曲线为例进行说明,如图7 和图8 所示。图7 中,低频段波峰是由于测试现场的供油油泵产生的较大噪声而带来的,因此从与仿真结果相近的第一个较大峰值开始,认为是实验得到的固有频率结果。图8 中的相干函数大部分在0.9 以上,确认了此次实验可信。通过对在滑台上表面及侧面进行实验得到的频率响应函数进行综合分析,得到了液体静压导轨的固有频率见表1。

表1 试验模态分析前4 阶固有频率Tab.1 Experimental modal analysis of front four-order inherent frequencies Hz


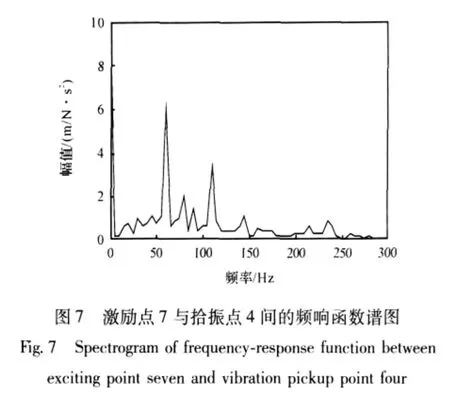

实验得到的导轨一阶固有频率为56.5Hz,该频率相对较低,静压导轨结构容易受到外界低频激励而产生较大的振动,对机床整体的动态特性也存在着影响,需要对导轨增加预紧力和载荷,以提高其固有频率。
3 仿真与实验结果对比分析
根据静压导轨实验模态分析结果,与对静压导轨有限元模型仿真得到结果进行对比,计算出了两种结果的相对误差。仿真模态分析结果、实验模态分析结果与相对误差见表2。

表2 实验模态分析与仿真模态分析前4 阶结果对比Tab.2 Comparison of results from experimental and simulation modal analyses of front four-order inherent frequencies
从上表中可以看出,除了第四阶固有频率的仿真结果与实验结果存在的差距较大外,其他三阶两种结果吻合较好。在测量时,滑台Z轴方向并未进行约束与每次锤击点的不同都会对实验结果产生影响。此外,由于有限元理论的离散化误差,对导轨幅板之间螺栓连接的忽略,以及采用弹簧单元模拟静压导轨刚度存在的误差等,使得仿真模态分析结果与实验模态分析结果之间存在着不可避免的偏差。虽然实验结果与仿真结果不是完全相符,但是二者的频率分布基本一致。
4 静压导轨的模态参数识别
模态参数识别有频域法和时域法两种,使用较多的是频域法。它是根据测取的频响函数估计值序列,依照一定的用模态参数表达的数学关系式进行。目前商用模态参数识别软件已经成熟,并得到了广泛的应用。但都是以对要识别的对象进行实验模态分析,得到频响函数为基础。陈学东等人采用了参数优化法,根据优化原理使理论模型的参数与试验模态参数的误差的加权累积量最小,即应用试验模态分析的结果修正有限元模型,使其模态参数与试验结果的模态参数基本一致[6]。本文利用实验中测量得到的频响函数曲线采用传统的半功率带宽法对液体静压导轨结合面的模态参数进行识别,其原理如图9 所示[7],依据公式(1)计算得到了结构的阻尼比ξ。

图9 半功率带宽法原理Fig.9 Principle of half-power bandwidth method

将文中得到的频响函数图谱作为静压导轨模态参数识别的频响函数曲线,根据公式(1)计算得到了导轨阻尼比。静压导轨前4 阶阻尼比见表3。
5 结论
通过对超精密机床中的液体导轨结构进行仿真和实验模态分析,得到了导轨结构的固有频率和模态阵型。其中仿真模态预测了导轨的固有频率并分析了结构的合理性,实验模态分析得到了准确的导轨模态参数并对有限元仿真结果进行了验证,从而证明了仿真方法在分析液体静压导轨的动态特性时是可行的。
本文中的液体静压导轨一阶固有频率为56.5Hz,需要施加预紧力和载荷以提升固有频率,防止在低频阶段发生共振。此外对实验结果采用半功率带宽法进行分析,得到了导轨的阻尼比,这些对全面掌握静压导轨的性能非常重要,可为液体静压导轨的设计与使用提供参考依据。
[1]N.C.Das.A Study of Optimum Load Capacity of Slider Bearings Lubricated with Power Law Fluids.Tribology International.1999,32:435-441.
[2]沈晓庆,翁泽宇,杨托,等.数控机床滚动导轨结合面参数的特性分析[J].机械制造,2009,47(2):30-32.
[3]Won-Jae Lee,Seok-ll Kim.Joint Stiffness Identification of an Ultra- Precision Machine for Machining Large-Surface Micro-Features[J].International Journal of Precision Engineering And Manufacturing.2009,10(5):115-121.
[4]陈学东.超精密气浮定位工作台技术[M].武汉:华中科技大学出版社,2007.
[5]师汉民.机械振动系统-分析·测试·建模·对策[M].武汉:华中科技大学出版社,2004.
[6]Xuedong Chen,Jin Lei.The dynamic modeling and dynamics response analysis of ultra-precision drive machine[J].Nano/Micro Engeered and Molecular Systems,2008:828-833.
[7]管迪华.模态分析技术[M].北京:清华大学出版社,1994.

