双桨双舵船横驶靠泊方案

陈锦标，封伟士，杨小军，肖英杰,，周伟

(上海海事大学 a. 商船学院； b. 航运仿真技术教育部工程研究中心， 上海 201306)

0 引 言

近年来，船舶日益大型化、快速化，配备传统单桨单舵的大型船舶的靠泊操纵越来越复杂.[1]为提高大型船舶的操纵性，减少靠离泊时对拖船、缆绳、锚链等的依赖，降低靠离泊成本，出现许多双桨双舵的大型船舶.目前，因双桨双舵船舶操纵模型具有较大的复杂性，对其靠离泊操纵方式研究成果较少.本文从MMG模型(由日本操纵运动数学模型建模小组提出)入手，建立双桨双舵船舶的靠离泊操纵模型，研究其靠离泊操纵方案.

MMG模型的主要特点是将作用于船体上的各个力分解计算.[2]本文基于MMG建模方法对双桨双舵船横驶靠泊进行受力分析，建立船舶运动数学模型.在此基础上对某一双桨双舵大型集装箱船的横驶靠泊方案进行研究，给出具体操纵方案.

1模型建立

为保障码头安全，对不同大小船舶的横向靠泊速度有不同要求.船舶越大，靠泊时可容许的横向靠泊速度越小.对开敞式码头，大型船舶、超大型船舶横向靠泊速度应控制在0.20 m/s以下；20万t以上的超大型船舶横向靠泊速度应控制在0.15 m/s以下(当横距泊位在100 m以内时，横向靠泊速度控制在0.10 m/s以内；在距泊位50 m以内时，应控制横向靠泊速度为0.03～0.05 m/s).靠泊的末段主要由多个拖船控制与协助.[3]根据双桨双舵大型船舶惯性大且靠泊时速度极低的特性，作如下假设:

(1)港池内水足够深且船舶运行速度较小，可不考虑浅水效应等.

(2)船舶受波浪影响较小，可忽略不计船舶的纵摇、垂荡及横摇运动.

(3)气象状况较好，即风、流均匀且较小，船舶进行自主靠泊.一般认为靠泊安全流速小于0.5 kn，最大不超过1 kn；靠泊安全风速小于3级，最大不超过5级.

根据以上假设，建立船舶运动坐标系，见图1.Ox0y0z0为空间固定坐标系，Gxyz是固定于船舶的运动坐标系，坐标原点G位于船舶重心.x轴指向船首为正，y轴指向船右舷为正，z轴垂直向下为正.[4-6]

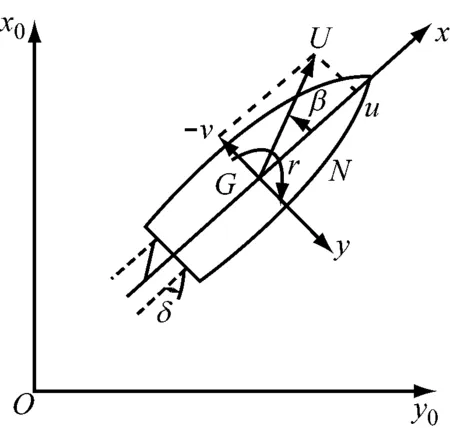
图1 船舶运动坐标系

MMG模型把附体坐标系原点取在船舶重心G，采用船舶操纵运动方程[5]为

(1)

式中：m为船舶质量;mx和my为船舶附加质量；u和v为船舶运动的速度分量；r为转艏角速度；X，Y分别为作用于船体x轴和y轴方向上的力；下标H为裸船体，P为桨，R为舵，A为风，W为流，B为岸壁，L为缆绳，T为拖船，S为艏侧推器，C为锚链.

根据上述假设，模型构造中无需考虑拖船拖力、锚力和缆绳的作用力，只考虑桨、舵、艏侧推器、风、流的作用力.

船舶航行中，螺旋桨的推力是主控力，用来克服水的阻力，维持船舶的操纵运动.根据MMG模型结果，在低速域时桨推力的模型[4]为

(0.7πnDP)2)CT(γ)

(2)

式中:tP为推力减额系数[7-8]；ωP为伴流系数；DP为桨径；n为转速；ρ为水的密度；γ为进速角;CT(γ)为实验系数.船用舵一般置于螺旋桨后，可以利用螺旋桨尾流增加舵效.在MMG模型中，作用于舵上的流体动力模型[5]为

(3)

式中：δ为舵角；FN为舵的正压力，可分解为纵向力FNsinδ和横向力FNcosδ;1-tR为舵的阻力减额修正系数[7-8]，

在航行中，舵处于两种不同的尾流中，即桨尾流和船体尾流,因此舵的正压力可表示为

FN=FN1+FN2=

(4)

式中：FN1和FN2分别为由桨尾流和船体尾流引起的舵的正压力；uR1和uR2分别为两种尾流速度；α1和α2分别表示两种尾流相对舵的冲角；η1和η2分别为A1/AR和A2/AR，其中，AR为舵面积，A1和A2分别为处于桨尾流中和处于船尾流中的舵面积；k(u)为速度修正参数[4]，当u≥0时，取值为1，当u<0时，取值为-0.75.

集装箱船舶具有较大的受风面积，风会对其操纵方式产生较大影响.风作用力表达式[4，9]为

(5)

式中：ρA为空气密度；vA为相对风速；AT和AL分别为水线上船舶正投影面积和侧投影面积；CAX和CAY分别为纵向和横向风压力系数.

船舶在港内航行时，与涨落潮流存在相对运动，船体受到水流的作用力.水流作用力的计算可类似于风作用力[4]，其表达式为

(6)

式中：AWf和AWs分别为水线下船舶正投影面积和侧投影面积；vW为相对流速；Cx(β)和Cy(β)为纵向和横向流压力系数.

2 双桨双舵船靠泊操纵数学模型

在低速域时操纵双桨双舵船与单桨单舵船的最大区别是：单桨单舵船在低速或速度为0时，舵效几乎为0，而双桨双舵船在低速域时，其双桨双舵及侧推器仍然可以配合使用.因此,双桨双舵船的操纵性比单桨单舵船好很多.理论上，若环境状况良好，桨、舵、侧推器配合得当，双桨双舵船可以不依靠拖船缆锚等的协助而实现自主靠泊.[10-11，13]以下是对双桨双舵船自主靠泊操纵的建模分析.

为实现向左横驶靠泊，船舶必须受到指向左舷的推力；为保证船舶、泊位的安全，必须克服船舶的纵向速度以及转艏角速度，即令u=0和r=0[12-13]，同时横向靠泊速度应较小.假定双桨双舵船的左桨以一定的功率倒车，左正舵；假定右桨进车，右舵固定一右舵角δ；艏侧推器进车[14].船舶受力分析见图2.图中左桨产生的拉力为XPl，左舵几乎无舵效；右桨产生的推力为XPr，由于右舵向右打一个舵角δ又处于右桨的尾流中，因此右舵产生的水动力分别为XRr(纵向)和YRr(横向).

图2 靠泊受力分析

对于内旋式双桨双舵船，当其左桨倒车右桨进车时，左桨排出流推船尾向右，右桨产生的横向力推船尾向左.这两个力可以相互抵消一部分，又因为这两个力比较小，所以它们的合力对船舶的作用可忽略不计.

在港区，大型船舶一般选择风、流均匀且较小的情况靠泊，以降低事故发生率.对于集装箱船舶，其正面受风面积较侧面受风面积小得多，若不是正横向来风，则力的作用重心一般偏离船舯(受力分析见图2，其纵向分力作用在x轴上，横向分力对船舶重心产生一个转船力矩).在港区，流一般平行于泊位，所以流对船舶的横向力较小.为保证靠泊安全，一般选择顶流靠泊，流的受力分析见图2.

图2中：bR为桨间距；xS为重心G到侧推器的距离；xPR为重心G到桨的纵向距离；xA为风力的作用点到重心G的距离；α为船首尾线与重心G到右(左)螺旋桨连线的夹角.

根据受力分析可知：若操纵适当，可以使桨、舵、风、流的纵向合力为0；艏侧推器产生推力YS，可以抵消船首偏转力矩，横向合力由桨舵侧推器的水动力和风的作用力提供，满足船舶自主靠泊操纵条件.为计算方便，将两个螺旋桨之间的相互干扰和舵到船尾的距离考虑为误差.根据MMG分离建模思想，可以单独计算每个螺旋桨和舵工作时产生的水动力，其经验公式见式(2)和(3).如图2所示，为克服纵向力和转艏角速度，建立数学模型如下：

式(7a)表示等式成立时纵向合力为0；式(7b)表示等式成立时，转艏力矩相互抵消；式(7c)是船舶重心处受到的横向力.若式(7a)和(7b)成立，式(7c)

不为0，则船舶操纵满足船舶自主靠泊条件，船舶横驶靠泊是可行的.用nl表示左桨转速，由于船舶纵向速度u=0，左桨产生的水动力[5]为

(8)

对于内燃机，倒车功率约为进车功率的85%[12-13]，所以左桨倒车产生的水动力应乘以85%.左桨倒车产生的拉力可简化为

(9)

其中

对于双桨双舵船，其左右桨对称，参数相同，因此CP也适应于右桨的水动力模型.假设nr为右桨转速，右桨产生的推力为

(10)

(11)

(12)

将XPl，XPr，XRr，XA，XW，YRr和YA代入式(7a)并化简得

(13)

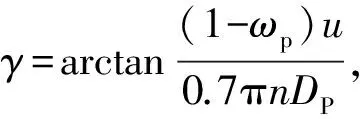
(14)

由上式可知，当舵角固定为δ，且左桨倒车转速和右桨正车转速满足上式时，可以满足式(7a)，使船舶的左右桨舵产生的纵向合力为0.为消除转艏力矩，满足式(7b)，艏侧推器应提供的侧推力为

(15)

船舶横向受横向合力FY，当船舶有横向速度时，还会受到横向水阻力YW，根据牛顿第二定律可以得到一阶微分方程

(16)

令CW=0.5ρAWsCy(β)，则YW=CWv2,v是船舶横向靠泊速度.求解上式，可得船舶速度达到v所需时间

(17)

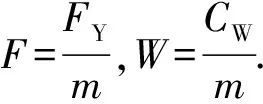
若操纵方案满足式(7)，则可以实现船舶的横驶自主靠泊.

3 方案研究

通过上面建立的双桨双舵大型船舶横驶靠泊模型，对某双桨双舵大型集装箱船在某实验港区的靠泊方案进行研究.

该船为内旋式双桨双舵大型集装箱船，螺距固定，满载排水量达25万t，配备艏侧推器.在前进时双桨产生的横向力在内侧产生干扰，在错车时，可以抵消部分横向力.考虑到该船为超大型船，在带缆前距泊位横距较小，因此将横向靠泊速度上限定为0.03 m/s.同时，考虑到该船为新型双桨双舵大型船，主机和侧推器功率较大，响应时间较小，故在操纵过程中不考虑船舶动力系统响应时间.该船资料见表1，车钟令见表2.

表1 实船资料

该船在某港区靠泊，泊位前沿线走向为000°→180°，该港区常年约有60%的风为西北向来风，流为涨落潮流，流速较低.假设该船左舷顶流靠泊，左桨倒车，左舵正舵；右桨正车，右舵右满舵；流速为1 kn左右.取风压合力系数为1.34[9,15]，流压力系数为0.3，海水密度ρ=1.025×103kg/m3，空气密度ρA=1.226 kg/m3，计量单位均采用国际单位制.根据上面建立的模型，在不同风况下对其操纵方案进行研究.

表2 车钟令

由表3可知，在侧推器的功率范围内均能使转艏力矩为0，但船舶设计时转速是阶跃性变化的，因此不能完全满足模型要求，所以纵向力不常为0.最佳动力配比方案为左桨倒车转速23 r/min，右桨正车转速21 r/min，艏侧推器应提供y轴正向69.53 kN的侧推力.操纵结果无转艏运动，纵向有微弱的后退速度，经过166 s后船舶横向靠泊速度将超过速度控制界限0.03 m/s.因此，操纵建议如下：靠泊前，先进车以施加一个向前的力，使船舶有微弱的前进运动，然后按此方案进行操纵，可抵消此方案产生的后退的力，应间歇式提供动力，根据操纵时间严格控制靠泊速度，保证靠泊安全.在无外力协助时，按以上建议方案在模拟器上进行模拟[16]，模拟横向速度为0.025 7 m/s(0.05 kn)左右，可以证明该模型所论证的操纵方案是可行的，因模拟器有一定的精度问题，所以模拟结果会有一定偏差.模拟器操纵结果见图3.

表3 无风、流情况下的操纵方案及其结果

图3 无风流情况左横移

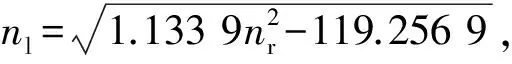
由表4可知，在这种风况下，虽然在侧推器功率范围内可以使转艏力矩为0，但纵向合力都较大，所以在此种风况下不建议自主靠泊.若借助外力如拖船的辅助，可选择左桨转速23 r/min，右桨转速21 r/min，侧推力y轴正向7.36 kN的操纵方案，此方案操纵结果纵向合力最小，侧推力较小，建议再借助较小的外力达到靠泊目的，降低靠泊成本.

表4 在风况一下的操纵方案及其结果

表5 在风况二下的操纵方案及其结果

由表5可知，在这种风况下，虽然仍不能完全满足模型要求，但可以选择多种操纵方案.方案一建议：左桨倒车转速27 r/min，右桨正车转速30 r/min，艏侧推器应提供Y轴负向128.13 kN的侧推力.此方案使转艏力矩为0，纵向有后退运动.按此方案，经过97 s后船舶横向靠泊速度将超过速度控制界限0.03 m/s，因此建议船舶在靠泊前先进车，使船有一前进的动量，可以抵消船舶的纵向运动.然后采用此方案，并间歇式提供动力，根据时间严格控制靠泊速度，从而实现横驶靠泊.方案二建议：左车倒车，右车进车，转速均为51 r/min，艏侧推器需提供y轴正向的148.36 kN的侧推力.按此方案，经过31 s后船舶横向靠泊速度将超过速度控制界限(0.03 m/s).此方案所需侧推器的功率较大，但纵向合力很小，纵向速度很小，因此若侧推器操纵控制合适，在船舶横向速度足够小的情况下，可以完全不借助外力进行横驶靠泊.

4 结束语

本文基于MMG建模方法，在多种环境状况下，对不受外力协助的双桨双舵大型船舶横驶靠泊操纵进行分析，建立靠泊操纵数学模型，并给出双桨双舵的动力配比和侧推力计算公式、超过应控制横向靠泊速度界限的操纵时间.然后在某一实验条件下，根据建立的数学模型，对某实验船的横驶靠泊方案进行研究.对3种风、流状况下的操纵方案进行分析，给出该船的最优靠泊方案，从理论上为大型船舶在有风和流影响、无拖船和锚协助时实现横驶靠泊提供一个可参考的操纵方案，可以降低大型双桨双舵船靠泊时的风险并减少靠泊成本，具有较大的可推广性.基于该模型可以继续对双桨双舵船操纵模型进行拓展研究.

当然，这个模型还有许多不足，如只考虑部分风、流情况，未将随机情况考虑在内，且风、流压力系数是类似船舶的实验结果，虽有一定的适用性，但不完全准确，会导致一定的误差.

对今后工作的展望：(1)考虑更多的环境条件对船舶的三维受力进行讨论，以达到更好的实景模拟效果；(2)对某一具体船型的船模进行水池风洞试验，实测各种相关系数，以提高模型精度；(3)将模型应用于越来越流行的模拟器上，辅助教学和实验研究.

参考文献：

[1] 吴冲. 集装箱船舶大型化规模经济研究[D]. 上海: 上海海事大学, 2005.

[2] 贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1998: 141-205.

[3] 彭国均, 刘洋, 张杏谷. 大型船舶辅助靠泊仪设计[J]. 交通运输工程学报, 2012(6): 18-54.

[4] 田超. 风浪流作用下船舶操纵运动的仿真计算[D]. 武汉: 武汉理工大学, 2003.

[5] KIM Y G, KIM S Y, KIM H T,etal. Prediction of the maneuverability of a large container ship with twin propellers and twin rudders[J]. J Mar Sci & Technol, 2007, 12(3): 130-138.

[6] OKAZAKI T, ISHIWATA A. Development of a ship maneuvering simulator to make maneuvering plan[C]//World Automation Congress (WAC), IEEE, 2012: 1-6.

[7] 杨盐生. 船舶阻力系数和推力系数的计算的数据库方法[J]. 大连海事大学学报, 1995, 21(4): 14-17.

[8] 李国定, 古文贤. 螺旋桨推力减额分数t值的研究[J]. 大连海运学院学报, 1990, 16(3): 251-254.

[9] 张金鹏. 大型集装箱风载荷理论分析及计算[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[10] 杜林海. 双桨双舵船舶港内操纵性研究[D]. 大连: 大连海事大学, 2004.

[11] 王化明, 邹早建. 双桨双舵船舶操纵性预报研究[J]. 武汉理工大学学报, 2006, 30(1): 124-127.

[12] 王诗洋. 舰船双桨双舵推进系统的水动力研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.

[13] 李日岭. 大型船舶自主靠泊方法的研究[D]. 大连: 大连海事大学, 2012.

[14] LEE S K, FUJINO M. Assessment of a mathematical model for the manoeuvring motion of a twin-propeller twin-rudder ship[J]. Int Shipbuilding Progress, 2003, 50(1): 109-123.

[15] 赵大明, 施朝健, 彭静. 应用扩展卡尔曼滤波算法的船舶运动模型参数辨识[J]. 上海海事大学学报, 2008, 29(3): 5-9.

[16] 王胜正, 施朝健, 石永辉. 新一代船舶操纵模拟器关键技术[J]. 上海海事大学学报, 2007, 28(1): 143-149.