基于SIHC仿真平台的船舶航向控制算法性能测试

蒋娇，李丽娜，陈国权,2，赵晴

(1. 集美大学 航海学院，福建 厦门 361021；2. 大连海事大学 航海学院，辽宁 大连 116026；3. 中国电信九江分公司，江西 九江 332000)

0 引 言

随着世界海运事业的发展，船舶数量越来越多，船舶朝大型化、高速化方向发展，船舶的航行安全显得越来越重要，这客观上推动着船舶导航与自动化驾驶技术的发展.船舶在海上航行受到风、浪和流的影响，故只有正确控制和使用船舵才能使船舶在各种外界影响下保持航向或者改变航向，从而保证船舶安全迅速地从出发地到达目的地.自动舵具有减少人力、节约燃料、降低机械磨损等功能.目前,船舶航向控制领域出现各类先进的控制算法.为设计满足不同指标要求及适应各种应用场合的航向智能控制算法，通过选择若干主流算法集成到船舶智能操控(Ship Intelligent Handling and Control, SIHC)仿真平台桌面系统进行性能测试.本文基于文献[1]和[2]实现的算法及文献[2]提出的控制算法评价方法，着重对该平台集成的两种航向控制算法进行初步的性能测试.

1 SIHC仿真平台简介

SIHC仿真平台是用于船舶航行自动化基础研究的仿真测试平台，其中的本船具有航向和航迹两种自动控制模式，能实现船舶自动避碰与航迹自动监控，可用于船舶智能避碰决策算法与智能控制算法测试.该平台实现以下创新点：智能目标船功能；先进的仿真技术；集成6自由度液压/电动平台；接入船舶自动识别系统(Automatic Identification System, AIS)交通流功能；标准电子海图平台.本文测试使用的是SIHC仿真平台的桌面系统，主要由1台主控台计算机、1台目标船服务器、4台本船计算机构成，本船集成有丹麦航海研究所(Denmark Marine Institute)开发的6自由度船模.

2 船舶航向控制算法原理

2.1 普通PID航向自动舵原理

6自由度船模自带有普通PID航向自动舵.基于其自带的船模参数，可以更好地确定PID的3个参数的初始值，从而达到较好的航向控制效果.普通PID航向自动舵结构及原理分别见图1和2.从图1可以看出，该自动舵实际上由一个传统的PID航向自动舵和一个滤波器组成.

图1 普通PID航向自动舵结构

图2 普通PID航向自动舵原理

普通PID航向自动舵控制规律的传递函数形式为

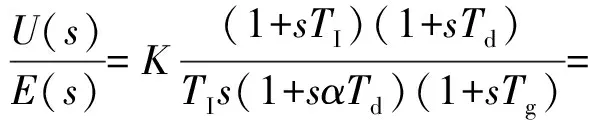
式中:U(s)为输出舵角；E(s)为输入航向偏差；K为舵增益；TI为积分时间常数；Td为反舵时间； 1/Tg为滤波频率；1/α为差异化系数.

2.2 模糊自整定PID航向自动舵原理

模糊自整定PID控制[1]运用模糊数学的基本原理和方法，把模糊控制规则的条件及其操作用模糊集表示，并把这些规则和有关信息作为知识存入计算机知识库中，然后根据控制系统的实际响应情况运用模糊推理，自动实现对PID参数的最佳调整[3].模糊自整定PID控制算法由模糊自整定PID控制器、限幅环节和被控对象等3个部分组成，其原理见图3.

图3 模糊自整定PID控制原理

模糊自整定PID控制算法在运行中不断检测误差e(t)=ψ(t)-ψr(t)和误差的变化率ec(t)=de(t)/dt，然后根据模糊规则(见表1～3)对PID的3个参数kp，ki，kd进行调整，以满足不同e和ec对控制参数的不同要求，从而使被控对象具有良好的动、静态性能.其中，ψ表示受控系统的航向角，ψr表示其设定值.

在船舶模糊自整定PID自动舵中，必须测量误差和误差的变化率即艏摇角速率ec.

在本设计中，作为输入的e和ec的论域为

e,ec={-5,-4,-3,-2,-1,0,1,2,3,4,5}

作为输出的修正量Δkp,Δki,Δkd的论域为

Δkp，Δki，Δkd={-5,-4,-3,-2,-1,0,1,2,3,4,5}

选取的输入、输出变量词集[4]为

e,ec,Δkp，Δki，Δkd={NB,NM,NS,ZO,PS,PM,PB}

词集中的元素依次分别代表负大、负中、负小、零、正小、正中和正大.

表1 Δkp的模糊控制规则[5]

表2 Δki的模糊控制规则

表3 Δkd的模糊控制规则

根据工程技术人员的技术知识和实际操作经验，本设计中输入、输出变量的隶属度函数曲线NB部分均取降半正态分布曲线，PB部分均取升半正态分布曲线，NM,NS,ZO,PS和PM部分均取三角分布曲线[6],因此可以得出各模糊子集的隶属度.根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计PID参数的模糊矩阵表，查出修正量代入式(1)～(3)：

在整个系统运行过程中，控制系统通过对模糊逻辑规则的结果处理、查表和计算，完成对PID参数的在线自整定.

3 航向控制算法性能评判方法

3.1 航向跟踪评判方法

为使船舶自动舵具有航迹(线)自动保持能力，必然要求自动舵具有航向跟踪功能，即在给定航向因接近计划航向的转向点需要改变的情况下，自动舵具有自动跟踪航向变化的能力.[1]

根据定值自动控制系统的性能指标及经验，航向跟踪的性能指标主要由超调量、跟踪响应速度、操舵次数、最大舵值和振荡次数组成.为得到这5个指标的权值，针对航向跟踪进行问卷调查.问卷中通过两两比较的方式让被调查者在速度快、精度高、耗油少等3个因素中选择最看重的因素.共发出问卷68份，速度快、精度高和耗油少被选中的次数分别为62，79和11.

问卷调查中的3个因素与这5个性能指标的相关程度有很大的差异：速度快是跟踪响应速度指标的最大关联因素；精度高是超调量指标的最大关联因素；耗油少是操舵次数、最大舵值、振荡次数这3个指标的最大关联因素.因此，可以分别算出5个性能指标的相应权值：超调量指标权值w1为0.45；跟踪响应速度指标权值w2为0.36；操舵次数、最大舵值、振荡次数这3个指标的权值w3，w4，w5理论上应该均为0.06.但是这5个性能指标的权值和不为1.经研究发现振荡次数指标比操舵次数和最大舵值这两个指标相对更重要，故其权值理应比另外两个大.以此得到超调量、跟踪响应速度、操舵次数、最大舵值、振荡次数这5个指标的权值依次分别为0.45，0.36，0.06，0.06，0.07.根据对船上工作人员的问卷调查，自动舵改向的最佳状态是零超调、无振荡、操舵两次、舵向改变10°时的响应时间控制在300 s以内、最大舵值不超过10°.故得出改向时自动舵的5个性能指标的隶属函数[10-11]如下：

超调量的隶属函数

f(x)=e-x2(x≥0)

跟踪响应速度的隶属函数

操舵次数的隶属函数

最大舵值的隶属函数

振荡次数的隶属函数

f(x)=e-x2(x≥0)

3.2 航向保持评判算法

船舶自动舵的航向保持功能是在给定航向不变的情况下能确保船舶在外界环境干扰作用下具有保持既定航向的能力.航向保持的性能指标主要由保向精度和舵机能耗组成.航向保持的性能指标为

式中：J为总体性能指标值；N为采样个数；ψ0(n)为设定航向；ψ(n)为实际航向；δn为当前舵角.对航向保持的评判主要从航向偏差和能耗方面考虑，所以J值越小，控制算法的航向保持性能越好.

为得到保向精度指标和舵机能耗指标的权值λ1和λ2，对一些有经验的船舶驾驶人员和航海教学人员进行一次问卷调查.在发出的58份问卷中，减少航向偏差和减少舵机能耗被选中次数分别为43和15，由此可以得出λ1和λ2分别为0.74和0.26.

4 评判结果及分析

4.1 航向跟踪测试方案与评判结果

考虑到不同船型及不同环境等因素，测试方案选取3种不同船型船模，即散货船、集装箱船和油船，另外为周全考虑又选取一条较小船模(巡逻艇)，船模信息见表4.环境设置分为8个等级，风向为40°，波浪周期为5 s，波浪方向为220°，具体的风速与浪高对应关系见表5.测试过程考虑流的影响，流速设置为1 kn，流向为120°.

表4 测试方案船模基本信息

表5 测试方案环境设置

在同一海域设置本船1和本船2，测试过程中两条船采用同样的船模.设定船舶的初始速度为该船的服务速度，船舶初始航向为0°，船舶航行全过程中其车钟都在FULL挡位.船舶开始运行后本船1和本船2分别采用模糊自整定PID航向自动舵和普通PID航向自动舵进行改向60°的操作，当两船航向改到60°且稳定后，结束测试.利用平台设计的接口，提取两船的数据，然后利用MATLAB分别画出两船的实际航迹向曲线.图4和5分别为船模III在环境7下的两种自动舵的实际航向及舵角变化曲线，其中，实线和虚线分别为普通PID自动舵和模糊自整定PID自动舵控制下的变化曲线.

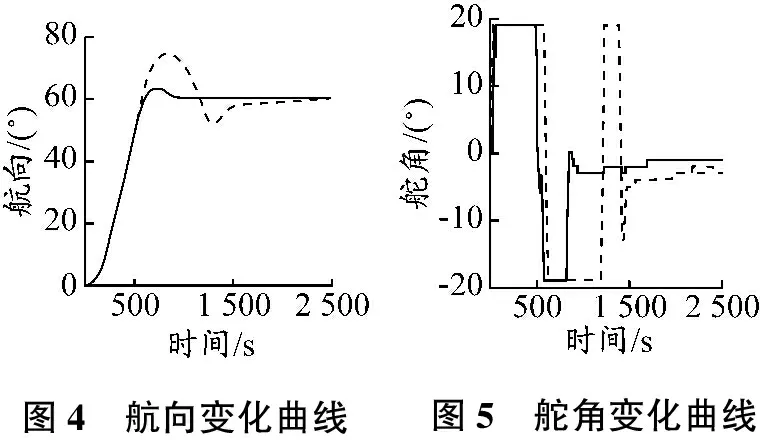
图4 航向变化曲线 图5 舵角变化曲线

再利用上述航向跟踪性能评判方法对每次实验数据进行处理，得到的评判结果见表6.

从表6可以明显看出，在不同环境下两种自动舵的控制性能基本接近，且稳定性都较好，但是在风浪等级较高的环境条件下亦或对于较小的船模，普通PID自动舵的性能稍好.同时可以看出，两种自动舵对不同船型的控制性能有明显差异(巡逻艇的控制效果最好，其次是集装箱船，对油船的控制性能最差)，这显示出两种自动舵对不同船型航向跟踪的适应性存在不足.

4.2 航向保持测试方案评判结果

航向保持测试方案的环境设置和船模选取与航向跟踪测试方案一致.在同一海域设置本船1和本船2，测试过程中两船采用同样的船模，设定船舶的初始速度为该船的服务速度，船舶的初始航向为60°，船舶航行全过程中其车钟都在FULL挡位.船舶开始运行后本船1和本船2分别采用模糊自整定PID和普通PID航向自动舵保向，当两船的航向都稳定在60°时，结束测试.根据第3.2节的航向保持评判算法，利用MATLAB对实验输出的船首向及舵角等数据进行处理，所得评判结果见表7.

表7 航向保持评判结果

由船模I和II的评判结果分析可知：在航向保持过程中本船1的总体性能指标值比本船2的小，即模糊自整定PID自动舵比普通PID自动舵有更好的航向保持性能.对于船模Ⅲ，普通PID自动舵的航向保持性能较好.由于船模IV较小，在风浪等级较高的环境下两种自动舵对其丧失航向保持能力.表7同时显示，模糊自整定PID自动舵对集装箱船的航向保持控制性能最好.

5 结束语

借助SIHC仿真平台开展船舶自动控制算法仿真及性能测试，利用MATLAB工具，分别从航向跟踪和航向保持两个方面对该平台集成的普通PID自动舵和模糊自整定PID自动舵的控制性能进行测试.从测试结果可知：在航向保持方面，就一般的船型而言，模糊自整定PID自动舵的性能优于普通PID自动舵；在航向跟踪方面，普通PID自动舵和模糊自整定PID自动舵的控制性能近乎一致；在某些环境下，普通PID自动舵对某些船型的控制性能会稍胜一筹，但对不同船型的适应性有待日后进一步优化.在航向控制评判算法方面，航向跟踪性能评判的隶属函数的临界值还有待于进一步细致优化，以更客观精准地分析比较不同船舶航向控制算法性能的优劣.

参考文献：

[1] 李丽娜, 杨神化, 熊振南, 等. 船舶拟人智能避碰决策理论框架的研究[J]. 中国航海, 2009, 32(6): 30-34.

[2] ZHAO Q, LI L, CHEN G. Research on fuzzy self-tuning of PID autopilot[C]//ICTE 2011, ASCE, 2011: 985-990.

[3] 赵晴. 船舶航迹智能控制算法的研究[D]. 厦门: 集美大学, 2012.

[4] 刘洋, 米伟, 郭晨. 船舶航向模糊自整定操舵控制器的研究[J]. 中国航海, 2010, 33(1): 71-75.

[5] 季本山. 基于PLC的模糊PID船舶自动舵[J]. 上海海事大学学报, 2009, 30(4): 57-62.

[6] 陈水利, 李敬功, 王向公. 模糊集理论及其应用[M]. 北京: 科学出版社, 2005： 42-58.

[7] 李丽娜, 张寿桂. 航海自动化[M]. 2版. 北京: 人民交通出版社, 2012: 70-83.

[8] HTIN Aung Kyaw, XIAO Yingjie. Assessment on the Yangon river channel based on fuzzy synthetic evaluation[J]. 上海海事大学学报, 2007, 28(1): 50-56.

[9] 陈辰, 胡甚平. 基于模糊DEA的航运公司安全管理有效性评价[J]. 上海海事大学学报, 2012, 33(1): 12-15.

[10] 张晓平. 模糊综合评判理论与应用研究进展[J]. 山东建筑工程学院学报, 2003, 18(4): 90-93.

[11] 陈锦标, 吴广宇, 应士君. 基于灰色模糊综合评估法的大型船舶模拟操纵评价[J]. 上海海事大学学报, 2008, 29(4): 1-5.