船舶自振特性分析
熊志鑫, 夏侯命胜, 张玉奎
(1. 上海海事大学 海洋科学与工程学院,上海 201306; 2. 中国船舶及海洋工程设计研究院,上海 200011)
0 引 言
上海海事大学的“48 000 DWT教学实习船”,是目前世界上投资规模最大、设施最齐全、设备最先进的教学实习船.除具备一般船舶的运输功能之外,其显著特征是集学生实习和实训功能、科学研究功能、国际交流功能于一身.教学实习船是真正意义上的大型远洋运输船舶,突出学生实习和实训功能,满足200余位师生员工的日常生活需求和教学活动的开展,为上海海事大学学生提供良好的实习平台,并用以培养各类高级航运人才.
由于船舶整体或局部发生共振会使人体感觉不舒服、导致船上精密仪器失灵和结构系统破坏等后果,因此有必要在设计阶段对大型多用途远洋船舶结构的总体和局部振动性能进行预报,了解这类船舶的结构动力响应特性,以便在结构设计方面采用合理方案和必要措施,以减轻结构振动的危害.
引起船舶振动的激励源有主机、螺旋桨、波浪载荷、风和流等,主要激励源是主机和螺旋桨.[1-5]因此,结构基频必须错开主要的激励频率,并且要有一定的频率储备.为了避免船体低阶振动频率与外界激励接近引起共振,要求总体振动1~3阶固有频率与主要的激励频率分别错开±8%~±10%,±10%~±12%,±12%~±15%.[6]若不满足频率储备要求,则需要进行振动响应计算或实船振动响应测量.基于上述要求,本文采用有限元混合模型对全船振动特性和上层建筑部位的振动进行计算分析和校核.计算内容包括全船结构自由振动计算.重点是确定全船结构的自由振动特性,避免船体主要激励源与船体自身结构的共振破坏,避免过度振动引起船上工作人员的工作和生活的不舒适.
1 船舶基本参数
1.1 主尺度
船舶主尺度参数及主机、螺旋桨参数见表1.

表1 船舶主尺度参数及主机、螺旋桨参数
1.2 船体梁基本剖面特性
表2列出各段船体梁的截面积A、垂向惯性矩Kv、水平惯性矩Kh和质量分布.表中,Mss和Mbs分别表示满载和压载时的船体质量.

表2 各段船体梁的截面积、惯性矩和质量分布
2 经验公式估算
船体总振动的固有频率是处理船舶振动问题的重要参数之一.通过固有频率与主机、螺旋桨等频率的比较,可以防止船体发生有害振动,避免产生共振现象.在预报固有频率时通常采用的方法[7-10]有以下3种:型船比较法、经验公式法、有限元法.对于教学实习船的振动情况,目前尚无可靠的母型船资料可查,所以采用后两种方法.
经验公式法是根据100余艘不同类型船舶资料归纳出的,适用于船长小于230 m的油船、干货船、散货船、矿砂船和客货船,一般情况下误差不大于7%.为了计算方便,本文在应用有限元方法计算时,采用船体梁模拟货舱和艏部结构.由于混合模型采取船体梁简化形式,不便进行全船扭转振动的计算.所以,采用经验公式算法既可以计算全船扭转振动固有频率,又能验证有限元混合模型法的准确性.以下即是根据船级社关于振动的计算要求,应用经验公式法对全船和上层建筑固有频率进行的估算.
2.1 经验公式法1
当主尺度和排水量已知时,船体梁垂向弯曲振动的前两阶固有频率
(1)
式中:i为船体梁垂向弯曲振动的节点数;fiv指节点数为i的船体梁垂向弯曲振动的固有频率;D为型深,m;L为垂线间长,m;B为型宽,m;aiv和biv为由船的类型和节点数确定的无因次因数,由表取得a2v=383,b2v=0.408,a3v=775,b3v=0.782;Kiv为船体横剖面对中和轴的惯性矩沿船长分布形式的变化,对固有频率影响的无因次修正因数,K2v=0.9+0.1Cb=0.985,K3v=0.85+0.15Cb=0.978;Eiv为船体桥楼对固有频率影响的无因次修正因数,E2v=1.028,E3v=1;Δv为包括附连水在内的船舶总质量,t;Cvm为船体钢材类型对船体振动影响的因数.
水平弯曲振动固有频率
(2)
式中:i为船体梁水平弯曲振动的节点数;fih指节点数为i的船体梁水平弯曲振动的固有频率;D为型深,m;L为垂线间长,m;B为型宽,m;aih和bih为由船的类型和节点数确定的无因次因数, 由表取得a2h=493,b2h=0.290,a3h=1 133,b3h=0.287;Kih为船体横剖面对中和轴的惯性矩沿船长分布形式的变化,对固有频率影响的无因次修正因数,K2h=0.9+0.1Cb=0.985,K3h=0.85+0.2Cb=1.021;Eih为船体桥楼对固有频率影响的无因次修正因数,E2h=E3h=1;Δh为包括附连水在内的船舶总质量,t;Chm为船体钢材类型对船体振动影响的因数.
2.2 经验公式法2
当中剖面惯性矩已知时,船体梁垂向弯曲振动的前两阶固有频率
(3)
式中:a2v=34 000,b2v=0.455,a3v=73 800,b3v=0.772;K2v=0.9+0.1Cb=0.985,K3v=0.85+0.2Cb=1.021;E2v=1.028,E3v=1;Iov为船体中剖面对水平轴的惯性矩.
水平弯曲振动固有频率
(4)
式中:a2h=34 000,b2h=0.455,a3h=73 800,b3h=0.772;K2h=0.9+0.1Cb=0.985,K3h=0.85+0.2Cb=1.021;E2h=E3h=1;Ioh为船体中剖面对水平轴的惯性矩.
2.3 全船扭转振动固有频率计算
全船扭转振动固有频率
(5)
式中:t为船体外壳板的平均厚度;Δ为船舶排水量.
2.4 上层建筑整体固有频率计算
上层建筑纵向振动固有频率
(6)
式中:fc为上层建筑纵向振动固有频率;fs为上层建筑仅作剪切振动时的固有频率;fr为上层建筑回转振动时的固有频率;K1和K2为上层建筑类型的修正因数, 由于本船特点符合规范中的A型结构,取值K1=0.9,K2=2.5.
以上所有参数选取,详细参照《船上振动控制指南》[11]相关内容.
3 有限元计算分析
经验公式法可以较方便地估算出一阶频率,但对于二阶及更高阶频率,则需要有限元方法进行计算.振动计算在全船有限元模型上进行,考虑到细长型船体的特点,机舱前部的主船体用变剖面的梁模拟.[12]艉部结构包括机舱、舵机舱、上层建筑内的围壁、平台以及主机座与主轴结构均在计算模型中予以表达,由细致的有限元模型描述,从而确保计算结果能比较真实地反映实际结构系统的振动形态.[13]
3.1 计算工况
教学实习船的全船自由振动响应计算以满载出港和压载到港两种装载状态分别进行.各装载状态的整体振动计算参数见表3(具体可参见船体设计装载手册).

表3 各装载状态振动计算参数
3.2 有限元模型
教学实习船的振动计算有限元船体梁混合模型完全依据各相关专业的设计图纸进行,前后处理分别运用MSC.Patran/Nastran完成.
图1为船体梁混合模型示意图,上层建筑、艉部和机舱结构采用三维有限元模型,机舱之前的结构(货舱和艏部)采用等效船体梁模拟.在等效船体梁与艉部结构连接处,采用剖面位移与转角的耦合加以模拟.其中,上层建筑、艉部和机舱三维有限元模型中包括船体的外壳、横舱壁、内底、纵桁和肋板等板结构,采用CQUAD4和CTRIA3壳体单元模拟;所有承受载荷的板上纵桁和加强筋等采用考虑偏心的梁单元模拟,并考虑适当的纵骨及加强筋等的合并;小的开孔结构及其周围加强筋以等效板厚的方法进行,且尽量依据实际形状模拟大的开孔结构.

图1全船有限元模型示意图
网格间距纵向一般为肋位间距,横向为纵骨间距;垂向的每一平台间为6个单元;双层底内的肋板腹板、桁材及舷侧翼板上的桁材沿其高度方向划分为2个单元.
船体梁由肋位#57开始,每10个肋位为1组,每组用一段梁模拟.各段梁的截面积和惯性矩由附近主要横剖面的截面积和惯性矩插值取得.
3.3 质量调整
3.3.1 船舶质量调整
振动计算不仅要考虑结构刚度,而且要考虑船舶质量,两者对振动计算结果的影响是并重的.[14]在船体各装载状态的重量调整中,船体自身重量的调整是通过调节单元结构的材料密度和施加典型结构质量点实现的.
3.3.2 附连水质量调整
附连水质量对船体振动影响很大,必须予以考虑.根据本文的模型情况,分别计算艉部和船体梁部分的附连水质量.
3.3.2.1 艉部附连水(船尾—#57)
艉部附连水质量通过软件自带的势流理论模块计算.
在MSC.Nastran软件内,通过定义有限元模型湿表面单元和吃水高度自动实现水动力质量的计算,其理论是用Helmholtz方法即边界元法(也叫源汇分布法)求解流体运动的拉普拉斯方程.源汇分布法的基本原理是选取一组在域内自动满足微分方程和给定边界条件的形状函数Ni,将未知函数u表示成此组函数的线性组合,即
(7)
式中:参数矢量α由所考察的边界条件确定.这样,无限域的问题变为一个离散化的边界问题,从而使自由度数目大大减少.
用边界元法时,流体的作用和结构物的运动(如振动)可视为在流固耦合面上具有分布的脉动源,近似离散成有限个点.假设流固耦合面上rj处单位面积的源强为σj,设它分布于Aj,则点ri的诱导速度矢量
(8)
式中:eij是从点j指向i的单位方向矢量,该速度势函数满足拉普拉斯方程.
另外,设i点的压力为pi,则压力方程
(9)
式中:ρ为流体的密度.将式(8)和(9)沿单元表面积分,得到矩阵χ和Λ及列阵u和F
u=χσ
(10)
F=Λσ
(11)
F为节点上的力,则得到质量矩阵
F=Mfu
(12)
式中:Mf为附连水质量矩阵
Mf=Λχ-1
(13)
3.3.2.2 船体梁附连水(船首—#57)
应用传统的船体梁固有频率计算公式如希列克公式、托德公式等(都是在大量实船测量值的基础上建立的)进行计算.
(1)船体作垂向振动时,各计算剖面处单位长度上的附连水质量
(14)
式中:Kiv为三维流动的修正因数,该因数取决于船的长宽比及振动阶数;Cv为附连水质量因数,取决于计算剖面形状及宽度与吃水比;bw为各计算剖面处的实际水线半宽.
(2)船体作水平振动时,各计算剖面处单位长度上的附连水质量
(15)
式中:Kih为三维流动的修正因数,该因数取决于船长吃水比及振动阶数;Ch为附连水质量因数,取决于计算剖面形状及宽度与吃水比;dw为各计算剖面处的实际吃水.
教学实习船是根据各个剖面相关参数,计算出各个剖面处在不同振动方向、不同阶数下的附连水质量的;然后根据船体梁计算要求对相应肋位剖面处的附连水质量进行叠加,最终得到每段船体梁的附连水质量.船体梁的附连水质量以非结构质量形式平摊到各段船体梁中.
3.4 边界条件
本文对教学实习船仅作整体振动计算分析,考虑附连水质量的影响,所以全船自由振动响应中的边界条件可以不施加,模拟船体自由飘浮于水中.
4 全船自由振动结果分析
4.1 计算结果的比较
表4和5为通过有限元分析法和经验公式法得出的压载到港和满载出港两种工况的全船固有频率,表6~8为两种不同工况下有限元法计算的全船典型自由振动频率值及全船自由振动频率和主机、螺旋桨激励频率的比较.

表4 压载到港工况下全船固有频率 Hz

表5 满载出港工况下全船固有频率 Hz
由表4和5数值比较可知,通过有限元船体梁混合法计算全船自由振动所得的固有频率与经验公式法所得的结果均在误差允许范围内;由表6~8可以看出,满载出港状态下,船体自由振动前3阶固有频率与主机和螺旋桨的激励频率错开比均在规范要求范围内;但是,满载出港状态下,全船第2阶垂向振动频率与桨轴频率仅错开7%,第1阶扭转振动频率与桨叶频率仅错开7.62%.
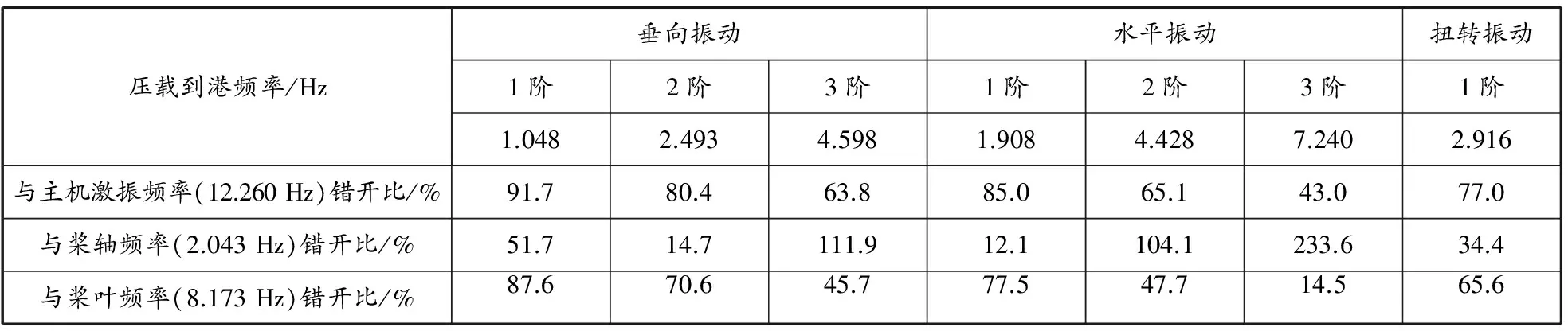
表6 压载到港工况下储备频率分析

表7 满载出港工况下储备频率分析

表8 上层建筑首阶固有频率(9.241 Hz)与激励源频率错开比
4.2 满载出港状态的全船典型自由振动模态振型图
图2~7为满载出港状态的全船典型自由振动模态振型图.
4.3 压载到港装载状态的全船典型自由振动模态
图8~13为压载出港装载状态的全船典型自由振动模态振型图.

图2 满载出港的1阶垂向振动模态(0.863 Hz)

图3 满载出港的1阶水平振动模态(1.578 Hz)
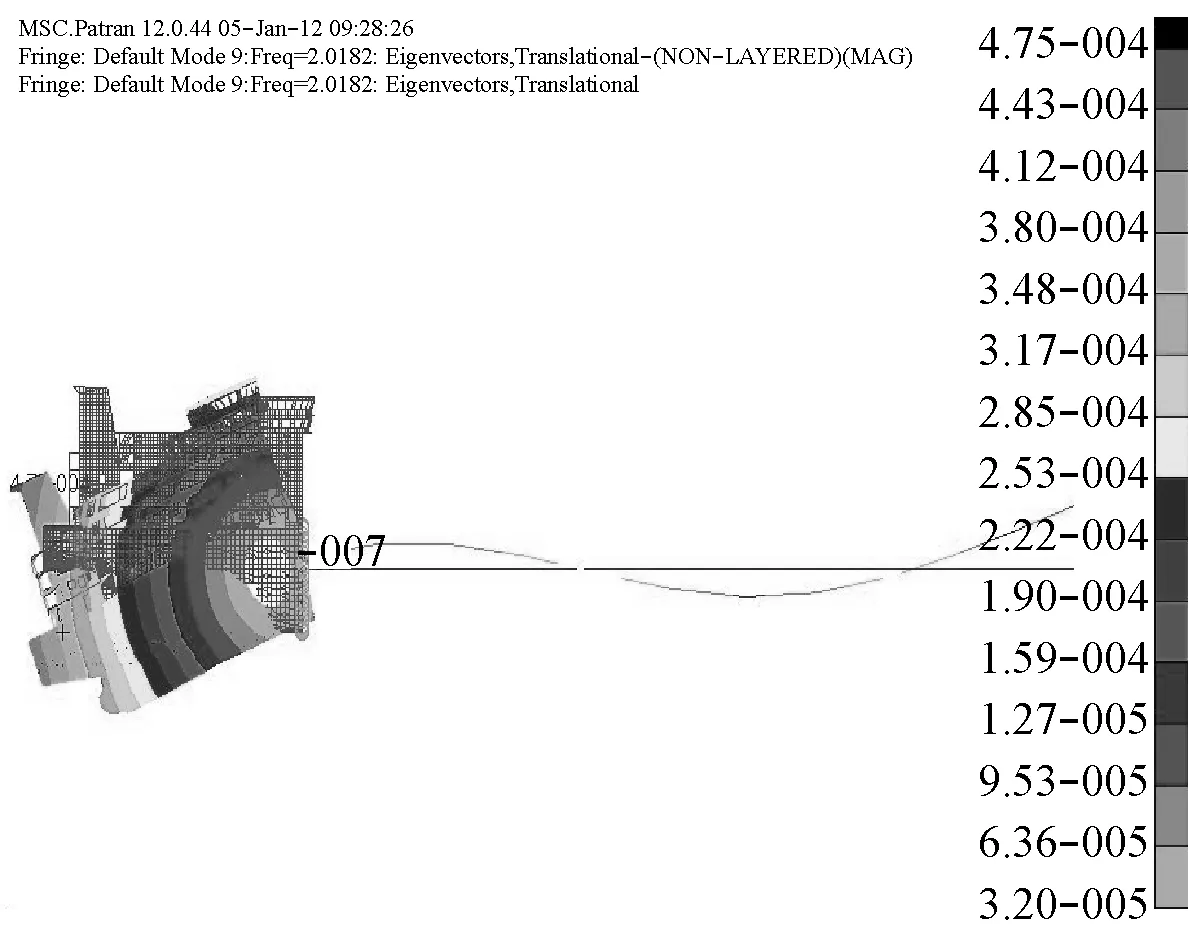
图4 满载出港的2阶垂向振动模态(2.018 Hz)
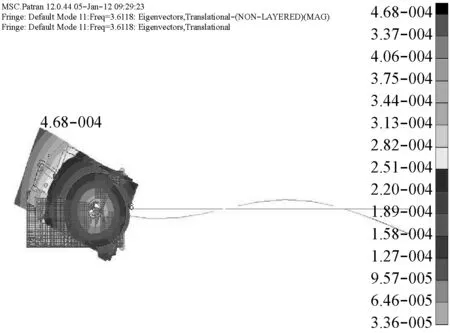
图5 满载出港的2阶水平振动模态(3.612 Hz)

图6 满载出港状态的3阶垂向振动模态(3.648 Hz)

图7 满载出港的3阶水平振动模态(6.381 Hz)

图8 压载到港的1阶垂向振动模态(1.048 Hz)

图9 压载到港的1阶水平振动模态(1.908 Hz)

图10 压载到港的2阶垂向振动模态(2.493 Hz)

图11 压载到港的2阶水平振动模态(4.428 Hz)

图12 压载到港状态的3阶垂向振动模态(4.598 Hz)
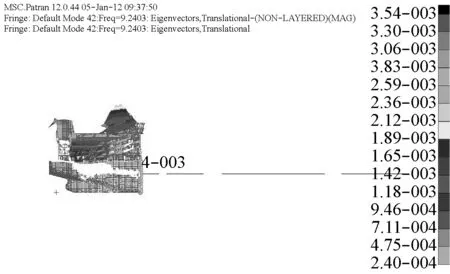
图13 上层建筑首阶纵向振动模态(9.241 Hz)
5 结 论
通过对教学实习船自振特性的计算结果分析,可以得出下述结论:
(1)采用艉部结构的细致有限元模型和机舱前部主船体结构的变剖面梁模型相结合的混合模型计算方法,并与经验公式的比较分析可知,该方法计算全船自由振动所得的结果可靠,并已用于实践,因此对船舶振动计算模型的建立具有一定的指导意义.
(2)在满载离港状态下,全船第2阶垂向振动频率与桨轴频率、第1阶扭转振动频率与桨叶频率较接近,应引起足够的重视,可作进一步的强迫振动分析.
(3)通过分析可知,教学实习船上层建筑1阶频率与主机及螺旋桨轴频率错开较大,避开共振的危险;与螺旋桨叶频率错开百分比略接近共振的数值范围,可以通过改进结构设计以提高上层建筑纵向剪切刚度和支撑刚度,进一步避开共振的范围.
参考文献:
[1] 邹春平, 陈端石, 华宏星. 船舶结构振动特性研究[J]. 船舶力学, 2003, 7(2): 102-115.
[2] 朱理, 庞福振, 康逢辉. 螺旋桨激励力下的舰船振动特性分析[J]. 中国造船, 2011, 52(2): 8-15.
[3] DALEY S, JOHNSON F A, PEARSON J B,etal. Active vibration control for marine applications[J]. Contro Eng Practice, 2004, 12(4): 465-474.
[4] KINNS R, BLOOR C D. Hull vibration excitation due to monopole and dipole propeller sources[J].J Sound & Vibration, 2004, 270(4/5): 951-980.
[5] CHO Dae-Seung. Design sensitivity analysis for vertical free vibration of hull girder[J]. Ocean Eng, 2007, 34(5/6): 902-907.
[6] 殷玉梅, 赵德有. 船舶上层建筑整体振动有限元建模方法研究[J]. 中国造船, 2009, 50(3): 49-56.
[7] KIM In-Il. A development of data structure and mesh generation algorithm for whole ship analysis modeling system[J]. Adv in Eng Software, 2006, 37(2): 85-96.
[8] LIN Tianran, PAN Jie, O’SHEA P J,etal. A study of vibration and vibration control of ship structures[J]. Marine Structures, 2009, 22(4): 730-743.
[9] SENJANOVIC I, TOMASEVIC S, VLADIMIR N. An advanced theory of thin-walled girders with application to ship vibrations[J]. Marine Structures, 2009, 22(3): 387-437.
[10] ZHU Suji, WU Mingkang, MOAN T. Experimental investigation of hull girder vibrations of a flexible backbone model in bending and torsion[J]. Appl Ocean Res, 2011, 33(4): 252-274.
[11] 中国船级社. 船上振动控制指南[S]. 北京: 人民交通出版社, 2000: 174-189, 225-227.
[12] 金咸定. 船舶结构动力学的进展与信息化[J]. 振动与冲击, 2002, 21(4): 1-7.
[13] 石慈忠. 大型自卸船船体振动研究[J]. 船舶, 2002(3): 36-41.
[14] 张新伟, 吴小康, 陆利平. 40万t矿砂船全船和局部振动研究[J]. 中国造船, 2011, 52(1): 26-38.

