果蝇算法优化的广义回归神经网络在变形监测预报中的应用

范 良，赵国忱，苏运强

（辽宁工程技术大学测绘与地理科学学院，辽宁阜新 123000）

一、引 言

变形监测正向自动化、实时化的方向不断发展，监测的对象和内容更加丰富，获得的观测数据越来越多，对变形数据的分析与预报有了更高的要求。作为一门迅速兴起的非线性科学，神经网络理论在处理信息十分复杂、背景知识比较模糊、推理规则不很明确的问题上，显示出了独特的优越性。广义回归神经网络（generalized regression neural network，GRNN）是美国学者 Donald F.Specht在1991年提出的，它是径向基神经网络的一种，在逼近能力和学习速度上较RBF网络有更强的优势，其模型的泛化性能良好。GRNN网络模型的形式不需要设定，隐回归单元中核函数的光滑因子的取值对网络输出影响比较大，但是难以确定。

为此，出现了模拟退火优化算法、遗传算法、蚁群算法及粒子群算法等各种优化算法，人们将这些算法应用到神经网络预报模型中，从而提高了变形数据处理预报的精度。但这些算法不能总是收敛到全局最优，而且迭代次数多、收敛速度慢。果蝇优化算法是模拟生物群体模型（果蝇）的群体智能优化算法，基于果蝇本身在感官知觉上优于其他物种，利用其觅食行为推演出寻求全局优化的能力更强。相对于粒子群等算法，果蝇优化算法需调整的参数少，更简单、更容易实现，试验证明其收敛到全局最优的能力更强。本文将果蝇优化算法用于优化GRNN的平滑因子，再利用该网络进行预测。采用实际的工程数据进行验证，并与未优化GRNN网络进行对比，验证此方法的有效性。

二、广义回归神经网络

广义回归神经网络的理论基础是非线性回归分析，设两个随机向量的联合概率密度函数为f（x，y），x的观测值为x0，则y对x0的回归值，即条件均值为

应用Parzen非参数估计方法，可以利用样本数据集{xi，yi}，i=1，2，…，n，根据式（1）估算密度函数f（x0，y）为

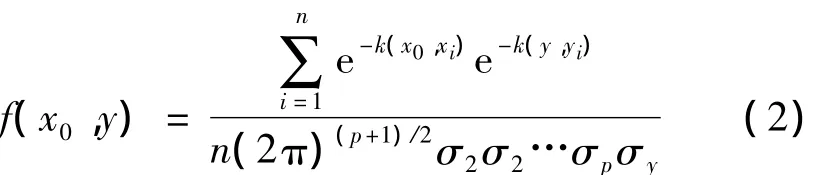
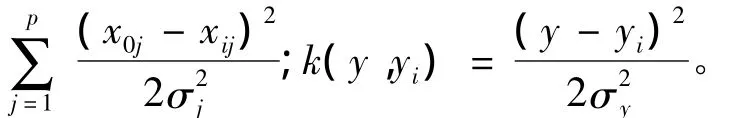
将式（2）代入式（1），交换积分与加和的顺序，经过计算可以得到

广义回归神经网络的结构如图1所示，它与RBF网络较为相似，是由输入层（input layer）、模式层（pattern layer）、求和层（summation layer）和输出层（output layer）4层构成的。输入层神经元数目等于样本输入向量的维数，直接将输入向量传递给模式层。模式层的单元数为n，这层的每个单元都对应于1个训练样本，一般采用高斯函数（e-k（x0，xi））为核函数，（xi）为各单元核函数的中心矢量。求和层包含分子单元和分母单元，分子单元将模式层各单元输出进行加权求和，其中的权是各训练样品的（yi）值；分母单元将模式层各单元的输出进行求和。输出层的单元将求和层分子、分母单元的输出相除进而算得y的估算值。

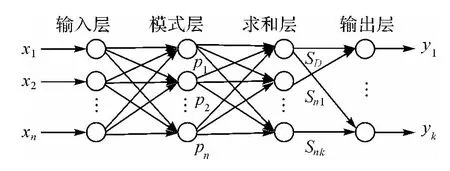
图1 广义回归神经网络结构图

三、果蝇优化算法优化广义回归网络

台湾学者潘文超教授提出的果蝇优化算法（fruit fly optimization algorithm，FOA）是根据果蝇觅食行为推演出来的全局寻优算法。

1.果蝇优化算法

果蝇在感官知觉，尤其是嗅觉和视觉上优于其他物种。果蝇的嗅觉器官能很好地搜集漂浮在空气中的各种气味，甚至能嗅到40 km以外的食物源。然后，飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且往该方向飞去。

依照果蝇搜寻食物的特性，结合图2，将其归纳为几个必要的步骤:

1）随机初始化果蝇群体的位置:

2）随机设置果蝇个体用嗅觉搜寻食物的方向与距离:

3）由于无法立即得到食物的具体位置，因此先估计此时果蝇个体与原点之距离，然后计算味道浓度判定值（S），此值为距离之倒数:

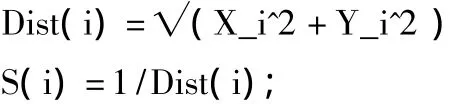
4）将味道浓度判定值（S）代入味道浓度判定函数（Fitness function），求出果蝇个体所处位置的味道浓度（Smell）:

5）求出果蝇群体中味道浓度的极值，并记录下此果蝇个体的位置:

6）果蝇群体利用视觉向步骤5）记录的位置飞去，形成新的群聚位置:

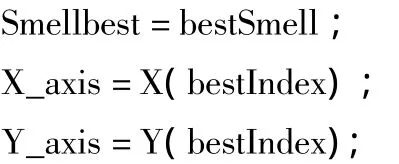
7）进入迭代寻优，重复执行步骤2）-5），并判断味道浓度是否优于前一迭代味道浓度，若是则执行步骤6）。

相比于其他经常被用作处理最优化问题的演算法，包括遗传算法（genetic algorithm）、蚁群算法（ant colony optimization）、粒子群算法（particle sarm optimization）等，果蝇优化算法有计算过程简单，便于将它的观念转化为程序代码，而且便于理解等优点。

图2 果蝇群体迭代搜索食物示意图

2.利用果蝇优化算法对参数Spread进行寻优

FOA优化GRNN的思路是透过果蝇的嗅觉随机觅食，再透过视觉而聚群在香味最浓的位置，可将GRNN的Spread参数值调整到最佳值，使网络输出值与目标值两者之间的均方根误差（RMSE）调整到最小。具体方法是先计算出果蝇个体位置与原点坐标（0，0）之间的距离并计算倒数以求出味道浓度判定值（S），再将它代入GRNN的参数Spread内，利用Matlab函数newgrnn（）训练网络得到输出值，并且根据样本观测值计算出RMSE（味道浓度判定函数），此值越小越好，保留此时的味道浓度判定值S，依此方法进行迭代搜寻。此外，Matlab训练GRNN网络的Spread值一般采用默认值1进行。

四、工程实例

本文采用Matlab编程，所用数据源为某煤矿煤仓的沉降量观测数据。这一观测时期为煤仓建成后生产使用中的状态。考虑影响变形的因子包括:温度，荷载及时效。其中，荷载因子取L（沉降观测时煤仓的装煤荷载量，以百分数表示）；时效影响沉降量的变化规律为初期变化急剧，后期渐趋稳定，时效沉降量变化一般符合对数函数，双曲线函数和线性函数，因此时效因子取M/100，InM，M/M+1（M为距离第一次测量时间天数）；温度分量T按照查询的当天气温为统计因子；输出数据为观测点的累计沉降量。本次使用数据总共51期，将前47期作为训练数据，后4期作为预测数据。

首先对输入输出数据进行预处理。利用Matlab自带函数mapminmax（）对样本数据进行归一化处理，使它们都在［0.1，0.9］之间，得出 FOAGRNN网络的输入输出数据列。

利用广义回归神经网络的Matlab工具箱，设计FOA动态搜寻最佳函数newgrnn（）的Spread参数值，建立FOA优化GRNN预报模型。果蝇群体大小为20，迭代次数为100，经Matlab仿真计算得出预报值。然后将Spread值分别设置为0.35、0.50、1，用相同的训练集训练网络，并对最后4期数据进行预报，分别得出预报值d'和绝对误差e，具体预报结果见表1和图3。

表1 预测结果比较表 mm

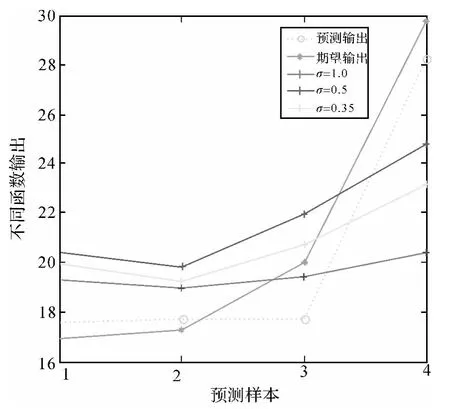
图3 预测结果比较图

经过对比分析可知，经由果蝇优化算法优化的广义回归神经网络可以迅速找到合适的Spread参数即光滑因子，预报精度得到了提高。

五、结 论

本文主要利用果蝇优化算法对广义回归神经网络进行优化，并建立了基于FOAGRNN的变形监测数据预报模型，它具有构造简单、调整参数少、训练过程快等特点。最后将FOAGRNN应用到实际数据中，可以发现:

1）果蝇优化算法具有构造简单、调整参数少、训练过程快等特点，算法实现程序容易实现，并且代码简单易懂，相对于遗传算法和粒子群算法，程序代码不会太过冗长。

2）果蝇优化算法能够以较高精度对数据进行拟合与预报，可以用来描述建筑物的沉降变化规律。

3）应用该模型对建筑物进行变形预报时，必须对原始数据进行预处理，而且用来预报模型的数据要尽可能多、规范、要经过过滤；否则个别质量较差的点会对预报结果产生较大影响。

4）经由果蝇优化算法优化迭代动态调整Spread参数值之后，预报能力得到提升，优于一般广义回归神经网络。

［1］ 陈永奇，吴予安，吴中如.变形监测分析与预报［M］.北京:测绘出版社，1997.

［2］ 张正禄，黄全义，文鸿雁，等.工程的变形监测分析与预报［M］.北京:测绘出版社，2007.

［3］ 潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估［J］.太原理工大学学报:社会科学版，2011，29（4）:1-5.

［4］ 肖正安.基于果蝇优化算法的模拟滤波器设计［J］.湖北第二师范学院学报，2012，29（2）:26-29.

［5］ 岳建平，方露，黎昵.变形监测理论与技术研究进展［J］.测绘通报，2007（7）:1-4.

［6］ 李钢.广义回归神经网络在大坝安全检测数据分析中的应用［D］.武汉:武汉大学，2005.

［7］ 兰海涛，李谦，韩春雨.基于广义回归神经网络的边坡稳定性评价［J］.岩土力学，2009，30（11）:3460-3463.

［8］ SPECHT D F.A General Regression Neural Network［J］.IEEE Transactions on Neutral Networks，1991，2（6）:568-576.

［9］ 史峰，王小川，郁磊，等.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010.

［10］ 潘文超.果蝇最佳化演算法—最新演化式计算技术［M］.台湾:沧海书局，2011.