全球电离层TEC数据统计分析与全局趋势分析

刘 康，王 枫，翟 旭

（中国地质大学（北京）土地科学技术学院，北京 100083）

一、引 言

电离层是指距地面60～2000 km的大气范围，在这一区域，自由电子、离子大量存在，严重影响无线电波等的传播。电离层总电子含量（total electron content，TEC）是反映电离层特性的主要参数。电离层TEC空间数据的挖掘与分析对消除GPS电离层延迟，保证无线电通信、广播电视、超视距雷达等系统的可靠运行，保障航天活动的安全，开发利用太空及维护人类的生存环境提供依据等诸多方面都有着重要的应用价值和科学意义。

电离层TEC是底面积为一个单位面积时，沿信号传播路径贯穿整个电离层的一个柱体内所含的电子总数，单位为电子/m2，有时也以TECU来表示，1TECU=1电子/m2。电离层TEC与日地关系非常密切，TEC随每天的时间、用户位置、卫星仰角、季节、电离通量、磁活动性、日斑周期和闪烁而变化。

二、全球电离层TEC数据统计分析

某一天的TEC数据为0:00—24:00每两小时间隔分为12个时间段，每两小时的数据都是经度从-180°每隔 5°变化到 180°，纬度从 -87.5°变化到87.5°，形成全球格网数据。下面以IGS发布的TEC数据为样本作时间和空间上的统计分析。

1.电离层TEC随时间日变化规律分析

图1是2010年5月20—22日这3天电离层TEC与地方时t之间的关系图。从图1可以看出，白天TEC含量随t逐渐增大，在下午4时左右达到最大值，随后又逐渐减小，在凌晨达到最小值。

图1 TEC日变化规律分析

2.电离层TEC三维空间分析

图2为2010年第80天（春分）两小时为一历元的TEC三维分布图。由图2可知全球电离层TEC形成峰值，图2（a）～（f）中TEC的峰值位置与当地时间14:00太阳直射点位置重合。

3.电离层TEC统计特性分析

下面以2010年第80天（春分）的14:00的电离层TEC为例说明其统计特性。结合图3具体分析如下，该时刻全球TEC的均值（132.171 3 TECU）大于中位数（97 TECU），说明存在部分离群的大值影响其分布的对称性；偏度为1.6903＞0，说明数据分布形态与正态分布相比为正偏或右偏，即有一条长尾巴拖在右边，数据右端有较多的极端值；峰度为5.4501＞0，说明该数据总体与正态分布比较为陡峭，数据分布为尖顶峰。由此可得出结论:电离层TEC为长尾、非对称的非正态过程变量。

三、全球电离层TEC全局趋势分析

球谐函数分析是地球物理分析中的一个重要工具，在地球基本磁场研究、重力和固体潮分析理论、地球自由振荡分析等方面得到了广泛应用。本文使用球谐函数和最小二乘的方法对TEC进行全局趋势拟合，即将每个经纬度点所在的TEC展成球谐系数的级数

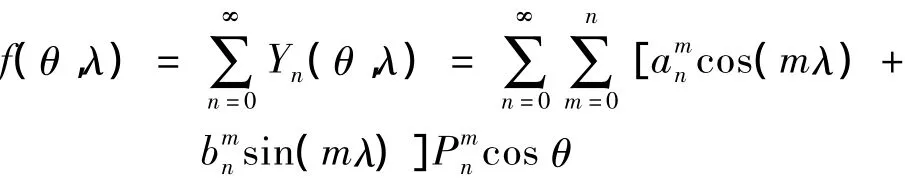
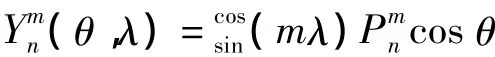
通过一系列点的经纬度λ、θ和对应的TEC值，可求出待定系数B。

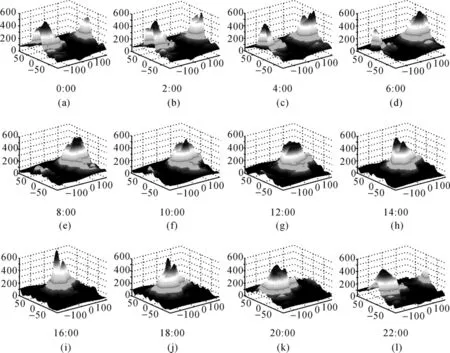
图2 2010年第80天（春分）每隔两小时的TEC三维分布图

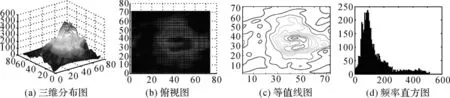
图3 2010年第80天（春分）14:00的电离层TEC的特性分析

用球谐函数拟合后，得到误差方程

根据最小二乘原理，得

由球谐系数B计算出的残差V并做残差值的直方图。根据残差值直方图的对称性及统计量确定球谐函数的阶数。如本例中，根据图4和表1选择对应直方图对称性最好，即均值和中位数最接近、标准差最小、偏度和峰度最接近0的阶数。通过对比分析可知，本例中9阶球谐函数最满足要求，其对应的残差的三维分布图及频率分布直方图如图5所示。

如图6（a）所示，本例中系数矩阵分布良好，9阶球谐函数共有100个参数，图中突起明显的各项作用显著，50个以后的参数作用微弱。B×x即为球谐函数拟合出的全局趋势部分，如图6（b）所示。由9次球谐函数拟合出较好的全局趋势，即以赤道为中心呈现双峰分布，有较好的对称性。

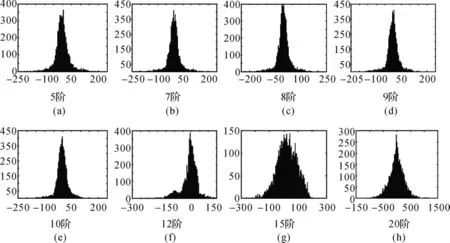
图4 不同阶数的球谐函数拟合后残差的直方图比较

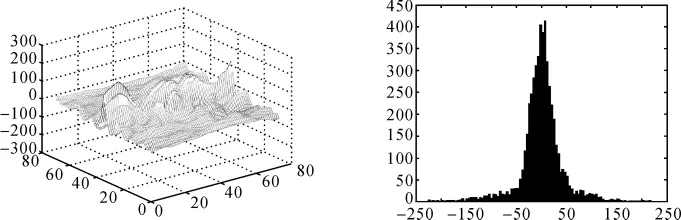
图5 9阶球谐函数拟合后残差的三维分布图及频率分布直方图

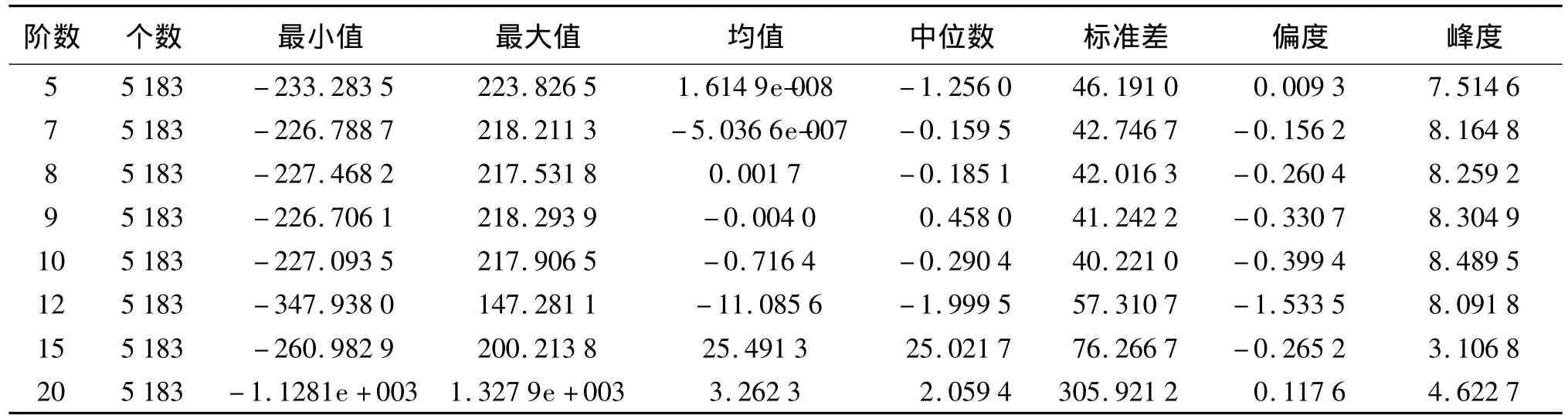
表1 不同阶数球谐函数所得残差的统计信息比较

图6 9阶球谐函数拟合出的全局趋势和系数矩阵分布图

四、结束语

本文对IGS分析中心发布的全球电离层TEC数据通过统计和球谐函数拟合进行数据挖掘和全局趋势分析。通过绘制某3天的电离层TEC含量随地方时的变化图，可以看出白天TEC含量随地方时逐渐增大，在下午4点左右达到最大值，随后又逐渐减小，在凌晨达到最小值；通过绘制全球TEC的三维图、全球俯视图、等值线图、频率直方图，并计算均值、中位数、偏度、峰度等统计量，揭示TEC数据在空间上的分布形态和规律；用球谐函数，采用最小二乘拟合来描述TEC的全局趋势，并根据残差的频率分布等统计特征确定9阶球谐函数最适合描述其全局趋势。

［1］ 秦昆.基于混合模型的空间数据挖掘及其应用［D］.北京:中国地质大学，2011.

［2］ 武文俊.电离层TEC预报模型的研究［D］.北京:中国科学院研究生院，2008.

［3］ 李猛.卫星导航定位系统主控站数据处理相关问题研究［D］.长沙:国防科学技术大学，2008.

［4］ 崔书珍.利用GPS数据研究电离层变化特性［D］.桂林:桂林工学院，2006.

［5］ 汤国安，杨昕.ArcGIS地理信息系统空间分析实验教程［M］.北京:科学出版社，2006.

［6］ 张志涌，杨祖樱.MATLAB教程［M］.修订版.北京:北京航空航天大学出版社，2009.