预条件共轭梯度法在地震数据重建方法中的应用

霍志周，熊 登，张剑锋

1 中国科学院地质与地球物理研究所，北京 100029

2 中国科学院大学，北京 100049

3 中国石油东方地球物理公司物探技术研究中心，河北涿州 072751

1 引 言

由于地表障碍物的存在（建筑物、道路、桥梁等）、地形条件的因素（禁采区和山区、森林、河网地区等）以及仪器硬件等问题的存在，引起地震数据在空间方向上的不规则采样．地震数据的不规则对DMO、FK 滤波、速度分析、多次波消除、谱估计和波动方程偏移等方法的处理结果带来了严重的影响．因此研究非规则采样地震数据的规则化对提高后续速度分析的精度、改善叠加效果、提升叠前偏移的质量等有着非常重要的作用．基于最小平方反演的Fourier变换地震数据重建方法是目前一种常用的地震重建方法［1－6］，本文通过将Fourier变换与贝叶斯参数反演方法相结合建立目标函数［7－9］，得到最小范数解．该方法的核心是对每一个频率成分求解线性方程组，从不规则采样地震数据中估计出重建数据的Fourier系数．可以使用共轭梯度法（Conjugate Gradient Method，CG）求解反演生成的线性方程组，由于该线性方程组的系数矩阵是Toeplitz矩阵，因此可以使用预条件共轭梯度法（Preconditioned Conjugate Gradient Method，PCG）［8，10］加快收敛速度，提高计算效率，保证解的稳定性．本文主要论述基于Toeplitz矩阵的循环预条件的构造方法［11－20］，以及在最小平方Fourier地震数据重建方法中的应用．

2 最小平方Fourier重建原理

通常地震数据在时间方向上是规则采样的，首先将地震数据从时间域变换到频率域．对于沿空间方向非规则采样的地震数据，为了求取空间波数，定义非规则离散傅里叶变换为

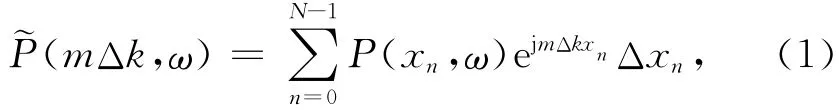
式中，Δxn＝（xn＋1－xn－1）/2，n＝0，…，N－1，xn表示空间采样点位置．如果直接用（1）式计算空间波数，则由于采样的非规则而引起误差．因此需要利用最小平方反演来消除误差．设带限地震数据的波数范围为 ［－MΔk，MΔk］ ，相应的波数域带宽为（2M＋1）Δk，波数域规则采样采样间隔为Δk，则由波数域重建任意空间位置xn的离散傅里叶反变换为

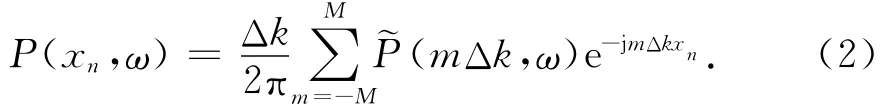
把上述离散傅里叶反变换当作正演模型．记系数矩阵为Anm＝，不规则采样地震数据为dn＝P（xn，ω），待求的规则采样波数为ω）．则将公式（2）写成矩阵形式为

在实际数据处理中，由于数据可能不完全是带限的，所以部分空间波数成分会超出定义的频带范围，这些超出的成分构成了上述正演模型的误差或噪音，因此在（3）式中需要噪声项

Duijndam 等［7］通过最小平方反演估计得到非规则采样数据d（xn，ω）的波数．从非规则采样数据向量d中计算出未知的规则采样的傅里叶系数向量可以归结为求解一个不适定线性反演问题．可以使用任何所需的参数估计技术，我们认为噪音和先验信息都是高斯分布的，假设噪音的协方差矩阵为Cn，平均值为零：n＝N（0，Cn），先验信息为＝．可以利用贝叶斯参数反演方法通过寻找后验概率密度函数的最大值来进行反演．后验概率密度函数为

其中p（d｜）是似然函数，p（）表示模型向量的先验分布．

求取p（d｜）的最大后验解转化为求下面目标函数的最小化的解

这里，Cn为噪音的协方差矩阵，C~p为先验模型的协方差矩阵．最小化目标函数得

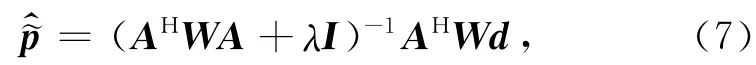
式中，为要计算得到的规则采样波数，Wii＝Δxi为权系数对角矩阵，AH和A分别表示Fourier正反变换矩阵，λ为高斯正则化因子．方程（7）左端的系数矩阵AHWA为Toeplitz矩阵，矩阵AHWA的病态程度受非规则采样数据之间最大间隔Δxa的大小来控制．最大间隔Δxa越大，矩阵AHWA病态程度越大，方程就越难以收敛．求解方程（7）最常用的方法为CG 算法，其中主要的运算是矩阵和向量相乘．因为系数矩阵为Toeplitz 矩阵，可以充分利用Toeplitz矩阵的特殊结构，使用Toeplitz矩阵与向量相乘的循环褶积快速算法［14］，通过快速傅里叶变换（Fast Fourier Transform，FFT）计算循环褶积来大大加快运算，该方法称为CG＋FFT 算法．很明显共轭梯度法迭代次数越多，解方程耗费的时间就越多，计算效率越低．因此需要引入预条件来改善系数矩阵的病态程度，以减少迭代次数．但引入预条件又为迭代法增加了额外的计算量，因此施加预条件需要把握预条件减少的解方程计算量和预条件本身增加的计算量之间的平衡，形成预条件还要考察预条件本身需要的计算量和内存需求．总体而言，预条件必须解决如下两方面问题：

1）预条件本身应该很容易构造和使用，即不需要花费大量计算时间构造预条件；

2）预条件系统应该很容易求解，即迭代收敛迅速．

预条件需要针对具体问题设计，不同的预条件有不同的特征值聚集能力．常规的Jacobi预条件和SSOR 预条件对我们的问题已经没有加速效果．因此我们转而寻求能满足如下条件的预条件：适用于致密矩阵计算，并且能充分利用Toeplitz矩阵的结构，能很好满足上述要求的就是循环预条件．循环预条件的最大优势就是利用FFT 计算预条件循环矩阵的特征值，这样在共轭梯度法计算矩阵与向量的除法时用特征值与向量FFT 简单相除即可．

3 Toeplitz矩阵的循环预条件

3．1 矩阵的预条件

对于求解大型线性方程组Ax＝b，加上预条件矩阵M，得到原方程组同解的方程组

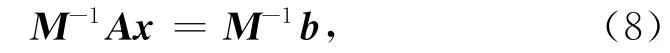
预条件方程组满足关系式

即矩阵M－1A的条件数远小于矩阵A的条件数．如果M对A的近似程度非常高，则通常M－1A的特征值接近1，谱半径为：ρ（M－1A）≤1，迭代计算时方程（8）就会迅速收敛．一般而言，实际计算中M－1A的特征值在某点（一般为1．0）附近集中程度越高，则求解方程（8）收敛速度越快．在共轭梯度迭代中加预条件时，并不需要计算矩阵乘积M－1A，而是在每次迭代时求解另外一个线性方程

其中rk＋1和zk＋1分别为共轭梯度第k＋1次迭代时的残差向量．

公式（10）计算时，若预条件M为循环矩阵，则可以利用循环褶积快速算法．当系数矩阵A为Toeplitz矩阵时，其循环预条件通常采用一定的规则从Toeplitz矩阵A中提取元素，并组合为循环矩阵，然后利用循环矩阵与向量相除的循环褶积快速算法，因此计算效率比大部分其它预条件都高．

3．2 常规循环预条件

考虑到通常Toeplitz矩阵的主对角线和其旁边的元素为强占优，可以简单的把前1/2列拷贝过来，再卷绕回去，作为循环预条件，称为Strang循环预条件［15］．循环预条件还可以通过使

达到最小化来定义，这里‖·‖F表示Frobenius范数，称为T Chan循环预条件［16－17］．

通常Strang 预条件矩阵本身条件数大于T Chan预条件．另外Strang预条件不能保持原系数矩阵的正定性，而T Chan 则能保证正定．虽然如此，但Strang预条件收敛速度并不一定比T Chan预条件慢．T Chan循环预条件由于能很好保持原系数矩阵的正定性，所以很常用．但由于T Chan循环预条件在实际应用中仍不能取得满意效果，所以通常不直接使用T Chan预条件，而是用来构造其它类型的循环预条件．

4 生成函数与循环预条件

4．1 生成函数

从数学角度可用生成函数来刻画Toeplitz矩阵的特征值分布情况．n×n阶的Toeplitz矩阵A的第j个特征值可以用生成函数f（x）在 ［－π，π］ 的取值f（2πj/n）来表示．令ak为Toeplitz矩阵A的第k个元素，aj，k＝aj－k，0≤j，k＜n，n≥1，则定义f为Toeplitz矩阵A的生成函数，有

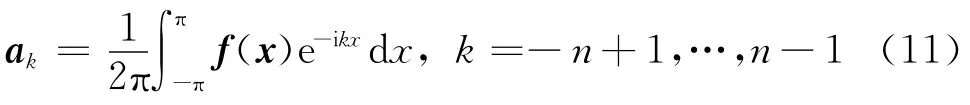
根据矩阵生成函数理论，良态Toeplitz矩阵的生成函数f（x）＞0，即为非负函数，由于特征值f（2πj/n）＞0恒成立，所以Toeplitz矩阵正定．病态Toeplitz矩阵是由于生成函数有零值．生成函数的零值越多，则Toeplitz矩阵病态越严重．相应地，使预条件后的系数矩阵具有更良态的谱，也等同于使该系数矩阵对应生成函数的零值减少或者完全没有．

病态Toeplitz矩阵的循环预条件C，从生成函数角度可以看作是用另一个正函数g（x）与A的生成函数f（x）进行褶积，以此对A矩阵生成函数中的零值进行匹配，同时保证褶积后的函数能收敛到f（x），即满足

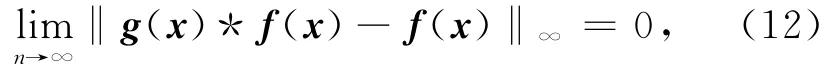
g（x）＊（x）作为C的生成函数，为f（x）的平滑近似，并且在xj＝2πj/n，（0≤j＜n）的取值应非常接近，这样能充分保证预条件矩阵C与原矩阵A非常接近．即有

满足上述关系后预条件系统C－1A的特征值就接近1，使预条件后的方程组迭代时能迅速收敛．满足该要求的g（x）均与δ函数很接近，如后文的高阶B样条核函数．用生成函数和一些核函数（如Dirichlet核、Fejér核）褶积，可以生成多种循环预条件，包括常见的Strang预条件、T Chan预条件等．其中Strang预条件可以看作是Dirichlet核与生成函数褶积后生成的，而T Chan预条件则能用Fejér核和生成函数褶积后生成．生成函数的优点是能够比较直观和真实的反映矩阵的病态程度．但根据生成函数与核函数褶积构造的预条件，在处理特别病态情况也即是原始矩阵生成函数有多个零值时，效果仍然不理想，因此还需要深入研究．另一个很关键的问题是，在构造生成函数预条件时，如果每次都要求推导Toeplitz矩阵对应的生成函数，则不但构成极大的计算负担，而且操作复杂，效率很低．因此，利用生成函数构造预条件的方法主要集中于不需要显式写出Toeplitz矩阵的生成函数，而是通过Toeplitz矩阵的元素与核函数作用就能直接构造预条件的方法．

4．2 广义Jackson核函数循环预条件

广义Jackson 核循环预条件［18］Kn，2r是用Toeplitz矩阵的生成函数与广义Jackson 核函数褶积，然后用褶积后的新函数作为生成函数，求取对应的循环矩阵作为原Toeplitz矩阵A的循环预条件．但是广义Jackson 核预条件方法不需要显式求出Toeplitz矩阵的生成函数．令x∈ ［－π，π］，定义Kn，2r（x）核函数为

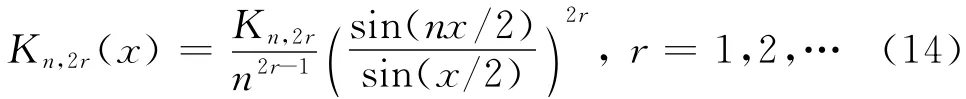
其中r为褶积核的阶数．Kn，2r为归一化常数，满足Kn，2r（x）dx＝1．广义Jackson 核函数作为循环预条件的优点是对所有正的r，n，都能保证生成的预条件是正定的．另外，高阶预条件可以由低阶预条件与自身褶积得到，这样构造预条件相对简单．

给定m×m阶Toeplitz矩阵A，其对应的广义Jackson循环预条件为m×m循环矩阵则有，即r（n－1）＜m≤rn．

核函数与生成函数褶积

其中

由上式可见，Kn，2r＊f仅仅依赖于元素ak．为了构造循环预条件，仅需要Kn，2r＊f在，0≤j＜m处的值，而不需要知道生成函数信息．

4．3 B样条循环预条件

B样条循环预条件［19］是将Toeplitz矩阵A的生成函数与B 样条函数褶积，将褶积结果作为生成函数，求取对应的循环矩阵作为预条件．B样条预条件方法也不需知道Toeplitz矩阵A的生成函数，而是直接提取A的元素aij与核函数进行组合．

为了构造循环预条件，定义B样条函数为

式中，cm为归一化常数，使Bm（0）＝1．则Bm（x）关于中心对称，．对任意m＝1，2，…，m阶函数Qm（x）在x＝0，1，…，m结点上定义为

基于Bm（x）的离散函数定义为

因此基于Bm（x）的B 样条循环预条件Cm定义为（只写出循环矩阵Cm的首列）

其中ak和－k为Toeplitz矩阵A中的元素．由此可见B样条预条件并不需要生成函数，而是直接与A中的元素作用．高阶B 样条预条件通常能更好适应病态Toeplitz方程组，但阶数高意味着预条件计算量的增加，可能会比较明显的增加求解方程组的时间，实际使用也一般就取到4阶．B样条函数具有很好的对称性，而且阶数越高，系数的函数图形越接近δ函数，对应B样条预条件矩阵与原矩阵A更接近，从而有更好的迭代加速效果．

4．4 其它核函数构造的循环预条件

沿用生成函数与非负核函数褶积构造新的循环预条件的思路，Chan［20］给出了几种核函数并推导了相应的循环预条件．我们选用了效果相对较好的两种循环预条件，对应的预条件矩阵C首列为

1）Hamming 循环预条件：

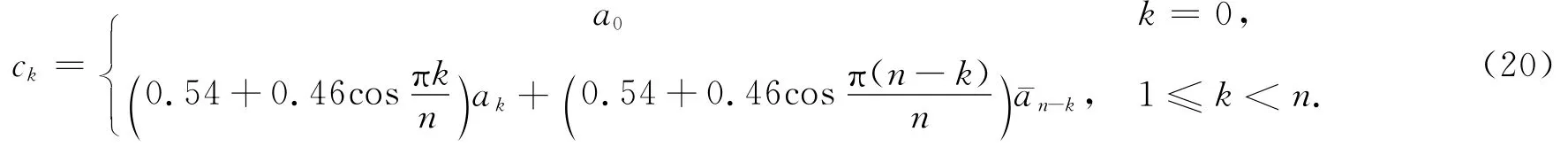
2）von Hann 循环预条件：

5 数值算例

本文提供两类数值算例，以验证所述循环预条件的收敛速度和处理病态Toeplitz矩阵的能力．所有的算例均采用预条件共轭梯度迭代法求解方程．迭代中止均采用误差限‖r‖2/‖b‖2≤1．0×10－7．通过观察需要的迭代次数多少，可以看出该预条件对病态矩阵的适应能力，以及不同循环预条件对同一问题收敛能力的相互对比．

5．1 生成函数构造病态Toeplitz矩阵

第一类数值算例从纯数学角度出发，根据给定的生成函数构造对应的病态Toeplitz 矩阵，将Toeplitz矩阵作为方程Ax＝b的A矩阵，b向量全设为1．令x∈ ［－ π，π］ ，则给定生成函数x2（π4－x4），对应的病态Toeplitz矩阵为T1，对应的元素为

表1为不同预条件求解T1x＝b需要的迭代次数．T1的行列大小见左边第一列．从第二列开始依次为以单位矩阵I为预条件（无预条件）、1 阶到4阶广义Jackson 核函数循环预条件（Kn，2，Kn，4，Kn，6，Kn，8）、3阶到5阶B样条循环预条件（B3，B4，B5），以及Hamming和von Hann核函数循环预条件对应的迭代次数．其中Kn，2对应T Chan循环预条件．如果迭代次数达到n次，共轭梯度还未收敛，则以“－”替代．由表1可见，预条件能大幅减少迭代次数．并且当n从32增加到512时，矩阵T1条件数也相应从4．1433×102增加到1．0154×105，但预条件迭代次数基本不随n的增加而增加．所以预条件对求解系数矩阵为病态Toeplitz 矩阵的线性方程组具有非常重要的作用．

表1 不同预条件求解T1x＝b需要的迭代次数Table 1 Iteration numbers for T1x＝bfor different preconditioned systems

图1为方程组T1x＝b当n＝32时的矩阵特征值分布，图中横坐标表示特征值模的大小，纵坐标没有特殊含义，当图中有多个预条件系统时，表示预条件系统的编号．对比可见，各种核函数循环预条件预后系统的特征值（图1（b—d））均有效地压缩了原病态Toeplitz矩阵T1特征值分布空间（图1a），预条件后的特征值系统均聚集在1．0左右．而且随着阶数增加，特征值在1．0左右聚集越多，从理论上讲需要的迭代次数应该更少，但实际求解需要的迭代次数并没有显著减少，这可能和相互间特征值分布差异仍然不够明显有关．

5．2 地震数据模型算例

为模拟地震资料处理中面临的病态反演情况，设计了一组随机分布的一维坐标来模拟个N非规则采样地震道的偏移距x．一维非规则采样地震数据的加权Fourier重建需要计算如下Toeplitz矩阵T构成的线性方程组：

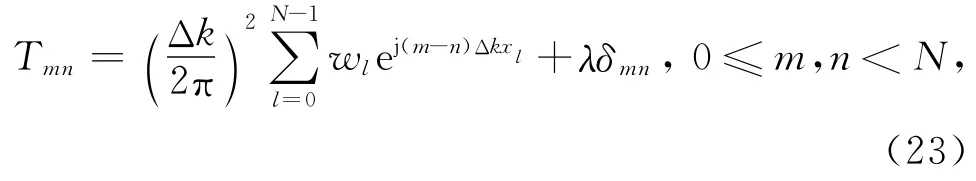
其中Δk＝2π/X为波数域采样间隔，X为排列长度，λ为Gauss正则化因子，取λ＝0．01，w为权系数．T的病态程度与排列的非规则采样程度相关．实验中对规则排列的xl（间距Δx）加上随机扰动量，计算中选取xl＝xl＋3Δx（0．5－rand（））．同样令b＝（1，1，…，1），求解方程组Tx＝b．取N＝32，64，128，256，512，计算迭代次数如表2所示．

表2 模拟Fourier重建非规则采样的反演迭代次数表Table 2 Iteration number by simulating Fourier reconstruction for irregular sampling

由表2可见，在处理该问题时，预条件还是有一定的效果．实际计算时发现即使Toeplitz矩阵大小达到了512×512，Toeplitz矩阵的特征值也很好的被压缩在2．0 以内．但是迭代次数上的优化则没有理论数据效果明显．而且与理论数据正好相反的是，高阶核函数反而没有低阶核函数的收敛效果好．因此对该类问题的预条件还需要进一步的探索．

图2为n＝32时方程（30）的特征值分布，图中横纵坐标和含义与图1中相同．可见预条件确实将病态Toeplitz矩阵的特征值进行了大幅压缩．但也可以看出高阶核函数在实际问题中没有起到更好的预条件效果，高阶和低阶核函数的预条件系统特征值分布差异很小．经计算发现，B 样条由3 阶到5阶，预条件系统条件数由66．1 上升至95．9；广义Jackson 预条件系统阶数由2 阶到8 阶，条件数由67．6上升至118．9，接近原始病态条件数159．4．因此高阶预条件不适用该问题的解决．

6 地震数据重建算例

首先我们选取SMAART 理论模型数据来计算，如图3a所示的一个单炮地震记录，总共有348道，其中有57 道是空道，图3b 为用最小平方Fourier方法重建的结果，可以看到地震数据被很好重建．图4中我们抽取其中的一道数据进行了重建前后的比较，可以看出重建几乎完全恢复了原始的数据．我们对某油田的一个实际二维共偏移距地震数据进行了重建，该数据总共有2278 道，其中有684是空道．为了便于清楚的显示地震剖面，图5a所示的是其中选取的300 道数据，时间轴从1．6s到3．6s．图5b为用最小平方Fourier方法重建的结果，可以看到重建道与原始道具有很好的连续性．图6a为重建前时间偏移的结果，图6b为重建后时间偏移的结果，对比两幅图可以看出，重建后的偏移剖面信噪比更高，构造更加清晰，同相轴的连续性也更好．表3给出了预条件共轭梯度法与几种常用的求解方法所需计算时间的比较，可以看出预条件共轭梯度法在求解速度上具有一定的优势．

图5 （a）含有空道的共偏移距地震数据和（b）最小平方Fourier反演的重建结果Fig．5 （a）Common offset seismic data containing null traces（a）and its reconstruction by the least squares Fourier inversion（b）

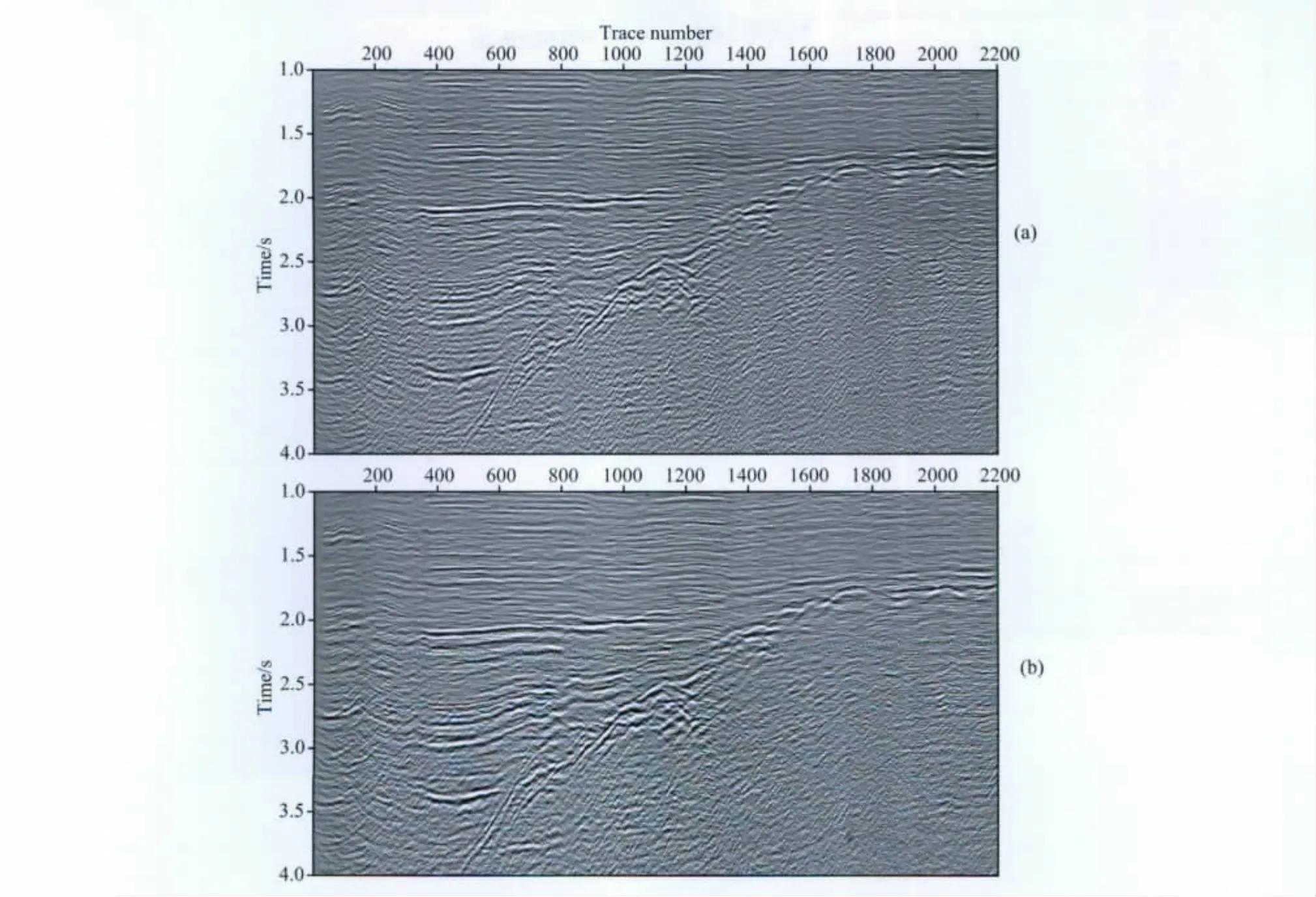
图6 （a）重建前数据的时间偏移结果和（b）重建后数据的时间偏移结果Fig．6 Result of time migration before data reconstruction（a）and result of time migration after data reconstruction（b）

表3 不同求解线性方程组方法的计算时间比较Table 3 Comparison of computing time for different methods of solving linear equations

预条件采用3阶B 样条循环预条件，以上算例运算结果均在Interl（R），Core（TM）2，Quad CPU Q9550 2．83GHz，内存2GB的微机上计算得到，操作系统为Centos4．7，编程语言为C．

7 结 论

本文针对最小平方Fourier地震数据重建方法所形成的线性方程组的求解问题，论述了Toeplitz矩阵循环预条件的基本理论，深入探讨了根据生成函数构造针对病态Toeplitz矩阵的循环预条件的方法，给出了2种核函数的循环预条件构造方式．用预条件共轭梯度法求解方程组，保证解的稳定性和提高了收敛速度．在最后我们给出了几组数值算例，验证了我们构造的预条件对理论数据具有明显效果，对实际数据也具有一定的效果．

（References）

［1］ Schonewille M A．Fourier reconstruction of irregularly sampled seismic data［Ph．D．thesis］．Delft：Delft University of Technology，2000．

［2］ 刘喜武，刘洪，刘彬．反假频非均匀地震数据重建方法研究．地球物理学报，2004，47（2）：299－305．

Liu X W，Liu H，Liu B．A study on algorithm for reconstruction of de－alias uneven seismic data．ChineseJ．Geophys．（in Chinese），2004，47（2）：299－305．

［3］ 孟小红，刘国峰，周建军．大间距地震数据重建方法研究．地球物理学进展，2006，21（3）：687－691．

Meng X H，Liu G F，Zhou J J．The study of reconstruction of large gap seismic data．ProgressinGeophys．（in Chinese），2006，21（3）：687－691．

［4］ 孟小红，郭良辉，张致付等．基于非均匀快速傅里叶变换的最小二乘反演地震数据重建．地球物理学报，2008，51（1）：235－241．

Meng X H，Guo L H，Zhang Z F，et al．Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform．ChineseJ．Geophys．（in Chinese），2008，51（1）：235－241．

［5］ Zwartjes P，Gisolf A．Fourier reconstruction with sparse inversion．GeophysicalProspecting，2007，55（2）：199－221．

［6］ Zwartjes P M，Sacchi M D．Fourier reconstruction of nonuniformly sampled，aliased seismic data．Geophysics，2007，72（1）：V21－V32．

［7］ Duijndam A J W，Schonewille M A，Hindriks C O H．Reconstruction of band－limited signals，irregularly sampled along one spatial direction．Geophysics，1999，64（2）：524－538．

［8］ 熊登．叠前地震数据规则化、重建及噪音压制［博士论文］．北京：中国科学院研究生院，2008．

Xiong D．Prestack seismic data regularization，reconstruction and noise suppression［Ph．D．thesis］（in Chinese）．Beijing：Graduate University，Chinese Academy of Sciences，2008．

［9］ 高建军，陈小宏，李景叶等．基于非均匀Fourier变换的地震数据重建方法研究．地球物理学进展，2009，24（5）：1741－1747．

Gao J J，Chen X H，Li J Y，et al．Study on reconstruction of seismic data based on nonuniform Fourier transform．ProgressinGeophys．（in Chinese），2009，24（5）：1741－1747．

［10］ 李冰，刘洪，李幼铭．三维地震数据离散光滑插值的共轭梯度法．地球物理学报，2002，45（5）：691－699．

Li B，Liu H，Li Y M．3－D seismic data discrete smooth interpolation using conjugate gradient．ChineseJ．Geophys．（in Chinese），2002，45（5）：691－699．

［11］ 梅金顺，刘洪．ω循环型边界条件．地球物理学报，2003，46（6）：835－841．

Mei J S，Liu H．ω－circulant boundary condition．ChineseJ．Geophys．（in Chinese），2003，46（6）：835－841．

［12］ 梅金顺，刘洪．Toeplitz方程组的近似计算．地球物理学进展，2003，18（1）：128－133．

Mei J S，Liu H．Approximate computation of Toeplitz systems of equations．ProgressinGeophys．（in Chinese），2003，18（1）：128－133．

［13］ 梅金顺，刘洪．预条件方程组及其应用．地球物理学报，2004，47（4）：718－722．

Mei J S，Liu H．Preconditioned equation sets and their applications．ChineseJ．Geophys．（in Chinese），2004，47（4）：718－722．

［14］ Chan R H，Ng N K．Conjugate gradient methods for Toeplitz systems．SIAMReview，1996，38（3）：427－482．

［15］ Strang G．Introduction to Applied Mathematics．Cambridge：Wellesley－Cambridge Press，1986．

［16］ Chan T F．An optimal circulant Preconditioner for Toeplitz systems．SIAMJ．Sci．Stat．Comput．，1988，9（4）：766－771．

［17］ Chan R H．Circulant preconditioners for Hermitian Toeplitz systems．SIAMJ．MatrixAnal．Appl．，1989，10（4）：542－550．

［18］ Chan R H，Yip A M，Ng M K．The best circulant preconditioners for hermitian Toeplitz systems．SIAMJ．Numer．Anal．，2001，38（3）：876－896．

［19］ Chan R H，Tso T M，Sun H W．Circulant preconditioners from B－splines．Proceedings to the SPIE Symposium on Advanced Signal Processing：Algorithms，Architectures，and Implementations VII，1997，3162：338－347．

［20］ Chan R H， Yeung M C． Circulant preconditioners constructed from kernels．SIAMJ．Numer．Anal．，1992，29（4）：1093－1103．