基于快速非抽样小波变换的岩屑多聚焦图像融合

张 影，王正勇，王 林，何小海

ZHANG Ying,WANG Zhengyong,WANG Lin,HE Xiaohai

四川大学 电子信息学院，成都 610064

College of Electronics and Information,Sichuan University,Chengdu 610064,China

1 引言

在高分辨率岩屑图像采集中，由于相机景深的限制和岩屑大小不一且表面凹凸不平，因此需要聚焦到不同平面采集多次，并通过多聚焦图像融合[1-2]处理才能得到一幅目标聚焦都清晰的岩屑图像。近年来，人们使用较多的是基于非抽样小波变换[3-4]的多聚焦图像融合。20世纪90年代后，人们将小波变换技术用于图像融合，取得了较好的融合质量。Liuetal在融合过程中增加了方向滤波器[5]，在进行小波变换时，分别对图像的行和列进行下采样。Nunezetal[6]提出非抽样小波变换方法，在进行小波分解的过程中去除了下采样。由于非抽样小波变换的平移不变性，且有效地抑制了振铃效应和Gibbs现象，融合过程可以逐层跟踪图像中的重要特征，有效避免了虚假信息的引入，因此受到了人们越来越多的青睐。然而，非抽样小波变换算法非常复杂，极大地延长了图像处理的时间，尤其对岩屑高分辨率图像的处理实时性非常差。

本文提出了一种基于快速非抽样小波变换的多聚焦图像融合算法，该算法仍然采用非抽样小波变换将图像转换到频域进行处理，同时针对空域直接对单个像素点处理上简洁、直观的特点，再将图像转换到空域上处理，非常有效地提高了图像处理的实时性，也一定程度上改善了图像的融合效果。

2 非抽样小波变换

非抽样小波变换是以抽样小波变换为基础，但是在每次分解时不进行下采样，因此每层变换后的高、低频图像与源图像大小相等。它利用小波系数之间的冗余性寻找与邻域系数之间的相关性，通过小波系数与邻域系数之间的关系来确定包含图像细节信息的非抽样小波系数[7]。目前最常用的非抽样小波正变换公式为[7]：

这里，A-1(x，y)为源图像对应的函数。式中的h(·)、g(·)分别对应于非抽样小波变换的低、高通分解滤波器系数，hi(·)、gi(·)分别对应于非抽样小波变换的低、高通重构滤波器系数，Aj(x，y)、Dj(x，y)为尺度 2j，位置(x，y)处非抽样尺度函数系数和非抽样小波系数，分别对应于非抽样小波的概貌子带、水平细节子带、垂直细节子带和对角细节子带。

显然，传统的非抽样小波变换的正、反变换算法都十分复杂，并且正、反变换的运算量也非常大。假如在非抽样小波变换融合过程中取消其反变换运算，那么将极大地提高图像处理的实时性。

由于非抽样小波变换没有抽样和插值的过程，且依次对图像像素点进行处理，因此对一幅图像进行非抽样小波变换后，每一层分解得到的一幅低频概貌图像、三幅高频细节图像都与源图像大小一样。所以，进行非抽样小波变换后的小波系数，不仅包含了源图像的所有特征信息，而且还存在一些冗余信息，而这些冗余信息便有利于寻找这些小波系数之间的依赖关系。假如对一幅二维图像进行N层非抽样小波分解，将得到(3N+1)个与源图像大小相同的小波系数图像，尤其对于本文处理的高分辨率岩屑图像，需要很大的内存空间，即对电脑的配置要求很高。然而经过深入研究，进行一层非抽样小波变换后得到的小波系数所包含的图像信息，足以满足后续图像融合的需求，因此本文算法采用非抽样小波一层分解。

3 快速非抽样小波融合算法

3.1 传统非抽样小波融合算法

基于非抽样小波变换的多聚焦图像融合算法主要是对不同分解层、不同频带的小波系数采用相应融合规则分别进行融合处理，然后再作非抽样小波反变换，即得到所需要的融合图像，如图1示。

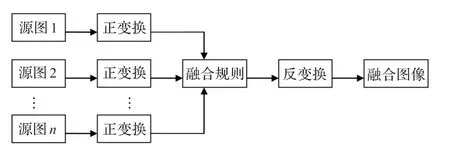
图1 传统非抽样小波融合算法

基于非抽样小波变换的图像融合过程中，决定融合结果质量的关键因素是处理高低频小波系数时采用的融合算法[8]。根据人眼对局部对比度变化较敏感的特点，在参与融合的源图像中选择显著边缘和线段等的清晰特征，并将这些特征保留到最后的融合图像中。因此，选择一种好的融合算法，对于图像融合的处理效果十分必要。

3.2 快速非抽样小波融合算法

多聚焦图像融合主要有基于空域和变换域两种方法。基于空域的多聚焦图像融合方法，不对参与融合的各源图像进行任何图像变换或分解，也就不存在因变换或分解而产生的信息损失，其原理简单易懂、计算量小。非抽样小波变换在每个分解层数据量保持不变，在逐层跟踪图像中的重要特征方面性能更强，并且具有线性相伴特性和空间坐标一致性，也使得按像素级[9]进行分析成为可能。因此，本文结合空域和变换域两种融合方法的优点，提出了一种基于快速非抽样小波变换的多聚焦图像融合算法。该算法从频、空域结合的角度对图像进行融合处理，基本思想是：设待融合图像分别为图像A和图像B，融合结果为图像F。首先对图像A和B分别作非抽样小波正变换，然后将得到的三个高频小波系数绝对值和作为融合规则，即：若图像A的高频系数绝对值和最大，则选取图像A对应空间位置的像素值作为融合图像F对应位置的像素值，否则，选取图像B对应空间位置的像素值作为融合图像F对应位置的像素值，如图2示。

图2 本文算法流程框图

具体步骤如下：

（1）分别对图像A和B进行非抽样小波一层分解，得到概貌子带 A0(x，y)、水平细节子带、垂直细节子带和对角细节子带

（2）分别计算待融合图像A和B对应像素点的高频系数绝对值和：

其中，K取为A、B。

（3）得到的融合图像F可表示为：

其中C为常数，一般取值为4.00～15.00，最优值取决于待融合图像。

针对人眼的视觉敏感特性，高频小波系数绝对值和越高，表明对应的边缘细节特征越明显，给人的视觉反映越直观。该融合规则能够识别源图像的特征，提取出不同源图像的清晰部分，获得一幅目标聚焦都清晰的融合图像。在理论上，传统的非抽样小波变换在进行正变换将图像由空域变换到频域上后，必须进行反变换再将图像变换回空域，显然，在反变换过程中必然造成一定的信息损失，又由于反变换算法十分复杂，这样不仅延长了图像的处理时间，而且也增加了图像的计算误差。本文算法取消了反变换，将融合后的结果直接应用于源图像，减少了处理过程中噪声等的影响，极大地提高了图像处理的实时性。它将频域与空域进行了完美的结合，取其各自的优点，提取出待融合图像的清晰部分，获得了一幅完全清晰的融合图像。

由于该融合规则是针对像素级融合，因此，在进行非抽样小波变换之前，待融合图像需要进行精确的配准。由于本文算法在获得融合结果后，直接对待融合图像进行处理，因此很大程度上减少了处理过程中噪声干扰产生的影响，增强了图像处理的鲁棒性。

另外，融合后的图像，有时会出现某像素点与周围相邻像素点来自不同源图像的情况，即融合图像的像素是不连续的，则需要对融合图像F进行一致性校验。即：选取3×3窗口，如果融合图像F中心像素点来自源图像A，而其周围8个邻域内来自源图像B的像素点个数大于或等于6，则将中心像素值置换成源图像B对应的像素值。该方法有效地提高了融合图像的连续性和抗噪能力。

其中，CA为以F(x，y)为中心的的3×3窗口内取自图像A的像素点个数，CB为以F(x，y)为中心的的3×3窗口内取自图像B的像素点个数。

4 实验结果及分析

非抽样小波变换将图像由空域转换到频域，提取出图像的概貌特征和边缘细节特征。融合规则是图像融合的核心部分，其算法的优劣将直接影响最终图像融合的效果。高频分量对应图像的细节信息，针对视觉敏感性，它能直接反映出图像的清晰度。

本文的实验环境：32位x86操作系统，Intel®CoreTMCPU i5-2400 3.09 GHz，3.23 GB的内存。

4.1 融合算法对比

在非抽样小波变换的基础上，将本文提出的多聚焦图像融合算法与几种基于非抽样小波变换的多聚焦图像融合算法进行对比实验。其中较常用的基于非抽样小波变换的多聚焦图像融合算法使用了以下5种融合规则，分别是：（1）三个高频绝对值和取大、低频取平均；（2）高低频分别取大；（3）三个高频绝对值和取大、低频依据梯度；（4）三个高频绝对值和取大、低频对比度取大；（5）三个高频绝对值和取大、低频在高频基础上判断。目前一种较新的多聚焦图像融合算法[1]：高、低频分别依据标准差、向量模值。

图3 原图及融合结果图

图3（a）～3（c）为依次由低到高聚焦的三幅岩屑图像，图像像素大小都为5 184×3 456，图3（d）为本文提出的基于非抽样小波变换的多聚焦图像融合算法的融合图像，采用的是一层非抽样小波正反变换。图3（e）～3（j）为以上提出的六种基于传统非抽样小波变换的多聚焦融合算法的融合图像（通过大量测试证明，当进行非抽样小波三层分解时，基于传统非抽样小波变换的多聚焦图像融合的融合效果相对较优，因此图3（e）～3（j）采用的是非抽样小波三层分解）。图3显示了截取的待融合图像和融合图像的小部分图像，表1为这些图像的融合质量评估。

表1 本文算法（非抽样）与几种常用非抽样小波融合算法质量比较

从图3和表1可以看出，不仅在直观视觉效果上，而且在平均梯度、信息熵、空间频域的客观数值评估上，本文提出的融合算法都优于其他几种非抽样小波融合算法。

4.2 融合时间对比

采用本文提出的多聚焦图像融合算法，对上述三幅待融合图像分别进行快速非抽样和非抽样小波变换，对比得到的融合图像及其融合时间。

图4（a）为本文提出的基于快速非抽样小波变换的多聚焦图像融合算法的融合图像。图4（b）为采用本文提出的融合算法的非抽样小波变换的融合图像（其中进行了一层非抽样小波正反变换）。图4为截取它们的小部分图像，表2为这两幅图像的融合质量评估。

图4 快速非抽样小波与非抽样小波融合结果图

表2 快速非抽样小波融合与非抽样小波融合图像质量比较

从图4和表2中可以看出，在直观视觉效果和平均梯度、信息熵、空间频域的客观数值评估上，这两幅融合图像的融合效果差别很小。然而，在融合时间上，基于快速非抽样小波变换的多聚焦图像融合远远快于基于非抽样小波变换的多聚焦图像融合，尤其对于高分辨率的的岩屑图像，快速非抽样小波变换具有非常明显的优势，很大程度上提高了图像融合处理的实时性。因此，在图像融合处理时间要求比较高的情况下，快速非抽样小波融合算法具有较强的实用性。

5 结论

本文分析研究了传统非抽样小波的正反变换算法，针对其对岩屑这样的高分辨率图像，处理实时性很差的缺点，结合频、空域的处理方法，提出了基于快速非抽样小波变换的多聚焦图像融合。文中比较了该融合算法与六种非抽样小波变换融合算法，并且对比了快速非抽样小波变换与非抽样小波变换的融合时间，实验结果表明，基于快速非抽样小波变换的多聚焦图像融合算法获得了比较好的图像融合效果，并极大地提高了实时性，具有较好的应用前景。

[1]Zhang Qiang，Guo Bao-long.Multifocus image fusion using the nonsubsampled contourlet transform[J].Signal Processing，2009，89（7）：1334-1346.

[2]Yang Shu-yuan，Wang Min，Lu Yan-xiong，et al.Fusion of multiparametric SAR images based on SW-nonsubsampled contourlet and PCNN[J].Signal Processing，2009，89（12）：2596-2608.

[3]Balster E J，Zheng Y F，Ewing R L.Feature-based wavelet shrinkage algorithm for image denoising[J].IEEE Trans on Image Processing，2005，14（12）：2024-2039.

[4]矫媛，黄斌文.基于上下文模型的非抽样小波图像去噪[J].科技信息，2010（19）：52-54.

[5]Kie B.Fusion of multiple images with robust random field models[J].IEEE，2003：335-338.

[6]Nunezetal J，Otazu X，Fors O.Multiresolution-based image fusion with additive wavelet decomposition[J].IEEE Transactions on Geoscience and Remote Sensing，1999，37（3）：1204-1211.

[7]靳士利，赵志刚.基于非抽样小波的多阈值去噪[J].青岛大学学报，2009，22（4）：77-81.

[8]李光鑫，王珂，张立保.加权多分辨率图像融合的快速算法[J].中国图象图形学报，2005，12（10）：1529-1536.

[9]李晖晖.多传感器图像融合算法研究[D].西安：西北工业大学，2006.