基于中间变量的乘子法

李 亮，孙 秦

LI Liang,SUN Qin

西北工业大学 航空学院，西安 710072

School of Aviation,Northwestern Polytechnic University,Xi’an 710072,China

1 引言

乘子法是求解约束优化问题的一类重要优化算法，该法最早由Powell[1]和Hestenes[2]于1969年针对等式约束优化问题同时独立提出，后又于1973年由Rockfellar[3]推广到求解不等式约束优化问题。该法的基本思想是在原约束优化问题的拉格朗日函数的基础上再加上适当的罚函数，从而将原问题转化为一系列的无约束优化子问题，并通过求解序列子问题的解来逐次逼近原问题的解[4-5]。

结构优化是一类典型的不等式约束优化问题，可以很好地用乘子法求解。在结构优化中，作为约束函数的应力、应变、位移、屈曲特征值等响应与作为设计变量的结构尺寸、坐标位置之间呈复杂的非线性关系，且变量往往存在于分母中[6-7]。为了降低约束函数的非线性程度，在对近似概念的研究中，Schmit[8]于1974年引入了倒变量作为中间变量，后来Fleury[9]又于1986年引入了混合变量作为中间变量。考虑到结构优化中设计变量值一般为正，本文将倒变量和混合变量这两种中间变量引入乘子法，提出基于中间变量的乘子法。中间变量可以降低无约束子问题的非线性程度，可以提高乘子法求解结构优化问题的效率和精度。

2 理论基础

2.1 乘子法

一般的结构优化问题可以表示为如下数学形式：

其中，x为设计变量的集合，f(x)为目标函数，cj(x)为约束函数，和分别为设计变量xi在设计空间中的下界和上界。此外，f(x)和cj(x)都是连续可微的，且问题（1）的可行域非空。

根据乘子法，可以将问题（1）转化为如下形式的增广拉格朗日函数：

其中，λ=(λ1，λ2，…，λm)T为非负的拉格朗日乘子向量，σ为正的罚参数，这两个量的初值由人为给定。边界约束可以在线性搜索中得到满足，因此未加入到增广拉格朗日函数中。

由式（2）可在点xκ处构造如下无约束子问题：

有多种方法可用于求解子问题（3），本文采用拟牛顿法。将求得的解记作xκ+1，若xκ+1满足如下收敛条件：

则将xκ+1作为原问题（1）的近似极小点。其中，ε是人为设定的收敛阈值，0＜ε＜1。否则，则按如下形式更新拉格朗日乘子向量λ和罚参数σ的值：

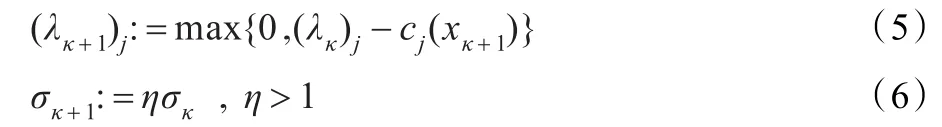
并在点xκ+1处继续构造无约束子问题，依此迭代，直到收敛。

2.2 拟牛顿法

拟牛顿法[10]是求解如下形式的无约束优化问题的一种重要方法：

该方法的其基本思路是，在当前迭代点xk处构造如下二次近似子问题来近似原问题（7）：

再求解子问题（8）并用其解dk作为搜索方向，即有：

其中，gk是 f(x)在点 xk处的一阶偏导数，Gk是 f(x)在点xk处的Hesse阵，Hk是Hesse阵逆的近似。Hk可以用校正公式求得，本文采用如下BFGS校正公式[11]：

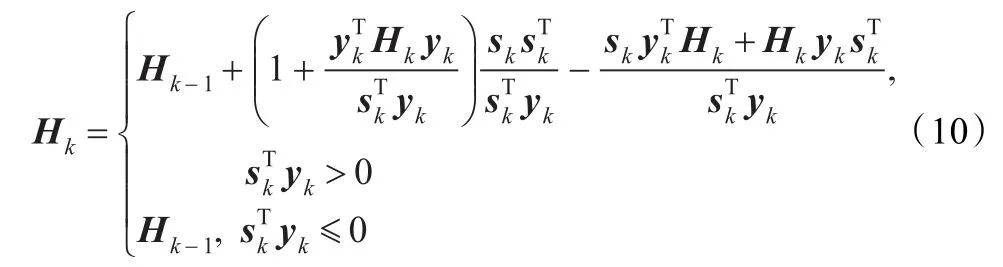
其中，yk=gk-gk-1，sk=xk-xk-1。

再沿dk做线性搜索，求得步长αk，得到xk+1=xk+αkdk。本文采用Armijo线性搜索技术[12]，并对其进行了改进，以保证搜索一开始就在设计空间内进行，算法步骤如下：

步骤1 给定0＜β＜1，0＜μ＜0.5，令 m1:=0，m2=20。

步骤2 求 p(i)=xk(i)+βm1d(i)，i=1，2，…，n。

若线性搜索求得的xk+1满足如下收敛条件：

则将xk+1作为问题（7）的近似解；否则，在xk+1处继续构造搜索方向，并求步长，以得到下一个点，依此迭代，直到收敛。

3 基于中间变量的乘子法

3.1 引入中间变量

本文引入了两种中间变量，即倒变量和混合变量。对于原变量x，若变量t满足：

则称其为x的倒变量；若变量t满足：

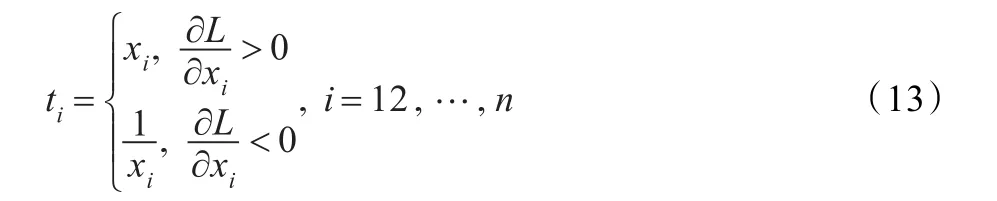
则称其为x的混合变量。

3.2 构造无约束子问题

引入了中间变量t，则原问题（1）可以化为：

其中，若ti是倒变量，满足式（12）中的关系，则有：

若ti是混合变量，满足式（13）中的关系，则有：

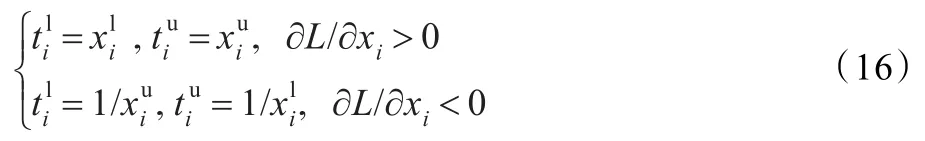
将问题（14）转化为增广拉格朗日函数形式为：

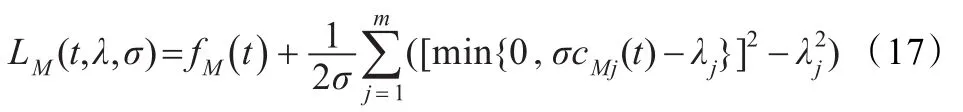
由式（17）可在点tκ处构造如下无约束子问题：

3.3 求解无约束子问题

在求解子问题（18）时，用拟牛顿法求搜索方向dk，用改进的Armijo线性搜索技术求搜索步长αk，以及用BFGS校正法构造Hesse阵逆的近似Hk，都是对中间变量t进行的。在求解中需要用到 fM(tk)和cMj(tk)的函数值和梯度值，求解方式为，若t是倒变量，满足式（12）中的关系，则

若t是混合变量，满足式（13）中的关系，则

将求得的子问题（18）的解记作 tκ+1。

需要注意的是，若采用的是混合变量时，由于不同迭代点处∂L/∂xi取值的正负情况并不一定相同，使得各迭代点处所用的混合变量的形式也会不同。因此，在用BFGS校正法构造Hesse阵逆的近似Hk时，为了获得前后两迭代点的梯度差，需要把两点处所用的混合变量的形式进行统一。本文的做法是，按当前点处的∂L/∂xi取值的正负情况来确定当前点和上一迭代点处所用的混合变量的形式。

3.4 算法的迭代和收敛

若tκ+1满足如下收敛条件：

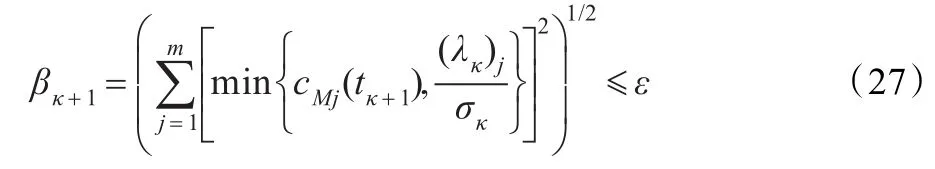
则将tk+1作为原问题（14）的近似极小点；否则，则按如下形式更新拉格朗日乘子向量λ和罚参数σ的值：

并在点tκ+1处继续构造无约束子问题，依此迭代，直到收敛。

4 数值算例

为了验证本文提出的基于中间变量的乘子法的计算效率和收敛性能，用Fortran语言编写了乘子法（MM）、基于倒变量的乘子法（RVMM）和基于混合变量的乘子法（MVMM）的计算程序，并用这三种方法分别求解了两个有一定非线性程度的算例[13-15]。为了保证算法的可比性，在求解同一个算例时，三种方法都采用相同的初始值和收敛阈值。

4.1 两杆桁架的形状优化

考虑一个如图1所示的两杆桁架的形状优化。该优化问题有两个类型不同的设计变量，其中x1定义为两杆的截面面积，x2定义为两杆下端点距离的一半。设计目标是杆的重量最小。设计约束施加在每个杆的应力上。

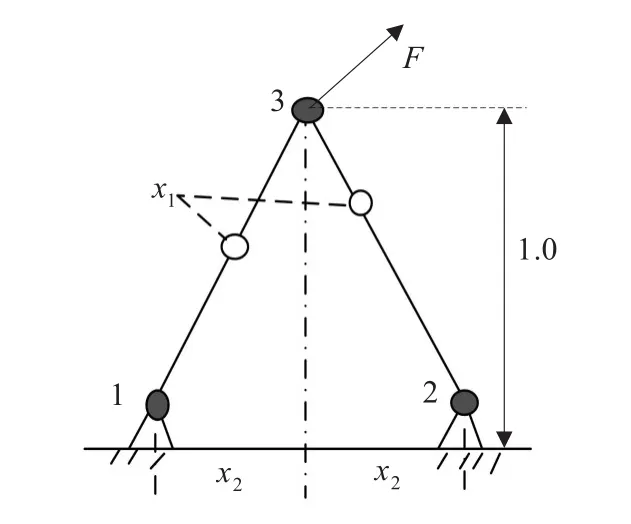
图1 两杆桁架

该结构优化问题可表示为如下数学形式：

以 x=(1.5，0.5)为起始点，用三种方法求解该问题，结果见表1。

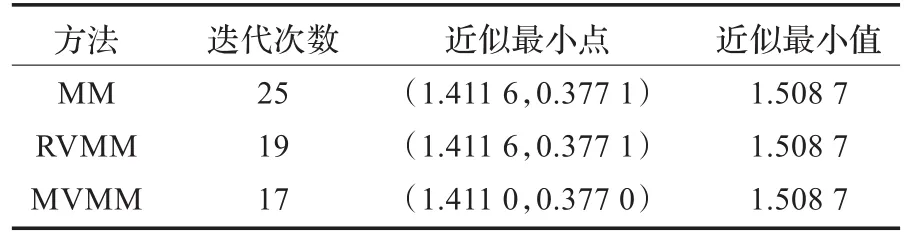
表1 两杆桁架形状优化结果

4.2 悬臂梁的重量优化

考虑如图2所示的悬臂梁的重量优化。这个梁分为5段，且每段的截面都是一个有给定均匀厚度的空心四方体。该优化问题有5个设计变量，分别定义为每个梁段的高度。设计目标是梁的重量最小。设计约束施加在梁顶端的位移上。

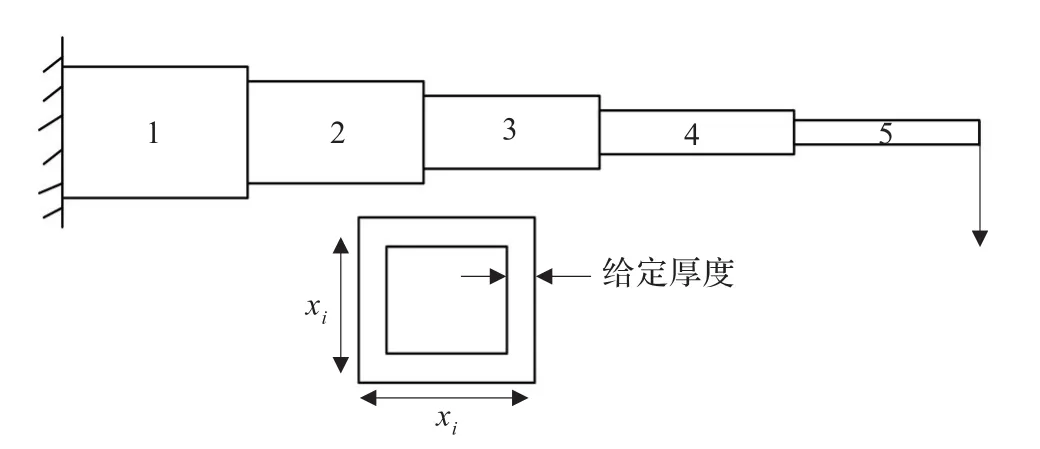
图2 悬臂梁

该结构优化问题可表示为如下数学形式：

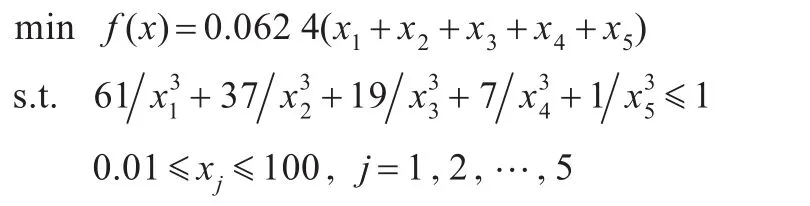
以 xj=5.0(j=1，2，…，5)为起始点，用三种方法求解该问题，结果见表2。

表2 悬臂梁重量优化结果

4.3 讨论

在两个算例中，三种方法都达到了收敛，且求得的近似最小点和近似最小值都很接近，这表明基于中间变量的乘子法具有良好的收敛性。

在两个算例中，RVMM和MVMM的迭代次数都少于MM的，MVMM的迭代次数都略少于RVMM的，这表明在求解结构优化问题时，基于中间变量的乘子法比一般的乘子法具有更快的收敛速度，而基于混合变量的乘子法的收敛速度比基于倒变量的乘子法略有提高。

在第一个算例中，RVMM和MVMM的迭代次数比MM的减少得较少，在第二个算例中则减少得较多。经分析，发现这个差别是由两个算例中目标函数和约束函数的结构形式的不同引起的。从两个问题的数学形式可见，与第二个算例相比，第一个算例中增广函数中变量在分子上占的比重更大、次方数更高；与第一个算例相比，第二个算例中增广函数中变量在分母上占的比重更大、次方数更高。事实上，若一个函数中变量在分母上占的比重越大、次方数越高，则引入中间变量代替原变量后，函数的非线性程度降低得也就越多。相反，若一个函数中变量在分子上占的比重越大、次方数越高，则引入中间变量后，函数的非线性程度降低得就没那么明显。如果一个函数中所有变量都只出现在分子上，则引入中间变量后，函数的非线性程度不但没有降低，反而会增大。因此，在结构优化问题中，若增广函数中变量在分子上占的比重较大、次方数比较高，则RVMM和MVMM的收敛速度与MM相比提高得就较少；而若增广函数中变量在分母上占的比重较大、次方数比较高，则提高得就较大。

5 结论

为了更有效地用乘子法求解结构优化问题，本文将乘子法与中间变量的概念相结合，提出了基于中间变量的乘子法。引入两种中间变量，即倒变量和混合变量，并详述了构造基于增广拉格朗日函数的无约束子问题，并用拟牛顿法、Armijo线性搜索法和BFGS校正法求解该子问题，以及实现拉格朗日乘子和罚参数的更新的算法流程。

两个数值算例的测试表明，基于中间变量的乘子法具有良好的收敛性，并比一般的乘子法具有更快的收敛速度。基于混合变量的乘子法的收敛速度比基于倒变量的乘子法有提高，但提高不显著。基于中间变量的乘子法的收敛速度，会受到优化问题中目标函数和约束函数的结构形式的影响。若增广函数中变量在分子上占的比重较大、次方数比较高，收敛速度就低些，而若增广函数中变量在分母上占的比重较大、次方数比较高，收敛速度就高些。

[1]Powell M J D.A method for nonlinear constraints in minimization problems[M].New York：Academic Press，1969：283-298.

[2]Hestenes M R.Multiplier and gradient methods[J].Journal of Optimization Theory and Applications，1969，4：303-320.

[3]Rockafellar R T.Augmented Lagrange multiplier functions and duality in nonconver programming[J].SIAM Journal on Control，1974，12：268-285.

[4]Bertsekas D P.Constrained optimization and lagrange multiplier methods[M].New York：Academic Press，1982：104-205.

[5]Nocedal J，Wright S J.Numerical optimization[M].New York：Springer-Verlag，1999：511-520.

[6]Venkayya V B.Structural optimization：a review and some recomm-endations[J].International Journal for Numerical Methods in Engineering，1978，13：203-228.

[7]Vanderplaats G N.Structural design optimization status and directon[J].AIAA Journal，1999，36：11-20.

[8]Schmit L A，Farshi B.Some approximation concepts for structural synthesis[J].AIAA Journal，1974，12：692-699.

[9]Fleury C.Structural optimization：a new dual method using mixed variables[J].International Journal for Numerical Methods in Engineer，1986，23：409-428.

[10]Wei Z X，Li G Y，Qi L Q.New quasi-Newton methods for unconstrained optimization[J].Applied Mathematics and Computation，2006，175：1156-1188.

[11]Yuan Y X.A modified BFGS algorithm for unconstrained optimization[J].IAM Journal of Numerical Analysis，1991，11：325-332.

[12]Shi Z J，Wang S Q.Modified nonmonotone Armijo line search for descent method[J].Numerical Algorithms，2011，57：1-25.

[13]Svanberg K.The method of moving asymptotes—a new method for structural optimization[J].International Journal for Numerical Methods in Engineer，1987，24：359-373.

[14]Yang D X，Yang P X.Numerical instabilities and convergence control for convex approximation methods[J].Nonlinear Dynamics，2010，61：605-622.

[15]Zhang W H，Fleury C.A modification of convex approximation methods for structural optimization[J].Computer&Structures，1997，64：89-95.