极软弱地层中开切眼导硐合理支护技术

梅凤清 韩立军 孟庆斌 李 云

(中国矿业大学深部岩土力学与地下工程国家重点实验室)

在极软弱地层中，开切眼导硐仅靠锚喷或锚网喷支护系统片面地提高支护强度难以实现巷道的长期稳定［1］，由此而出现了通过2种或2种以上的支护方式有机组合的联合支护方式［2-3］。但是，由于极软弱地层一般围岩较为松散，容易引起巷道应力集中，联合支护方式在使用过程中往往会出现许多问题。因此，研究基于锚网支护的新型联合支护技术意义深远。本研究以蒙东地区西一矿极软弱地层为背景，通过理论计算、FLAC3D和ANSYS数值计算、现场试验展开极软弱地层中开切眼导硐合理支护技术的探讨。

1 工程概况

蒙东地区西一矿煤矿目前主采3#煤层。煤层顶底板主要为胶结程度极差的泥岩、粉沙岩、砂岩等。煤层抗压强度最大值为20.1 MPa，最小值为2.9 MPa，平均值为8.77 MPa，为软煤～中硬煤类;顶、底板白垩系沉积岩抗压强度最大值为 51.8 MPa，最小值为0.1 MPa，平均值为6.05 MPa，为极软弱岩类。煤岩层力学性能低，且存在风化、泥化和崩解现象，围岩自承载能力较低，难以实施工作面开切眼导硐的支护，对开切眼支护及顶板控制造成极大影响。

2 合理支护方式的选择

为了探索开切眼导硐合理的支护方式，采用FLAC3D数值软件［4］模拟不同支护方式下巷道的支护效果以及对围岩稳定性的影响。研究1302工作面开切眼导硐在无支护、方案一(锚网支护)、方案二(锚网索支护)、方案三(锚网索+工字钢支护)等4种情况下围岩的塑性区分布及变形破坏特征，以确定合理的支护方案。开切眼导硐为4.5 m×3.2 m的矩形断面，埋置深度为255 m。数值计算过程中锚杆参数为∅20 mm×2 400 mm(间排距700 mm)，锚索参数为∅17.8 mm×6 000 mm(间排距为1 600 mm×2 100 mm)，型钢支架采用16#工字钢(排距为1 400 mm)。

2.1 塑性区分布

数值计算结果表明，无支护时，顶板冒落高度、底板和两帮破坏深度均较大，分别为3.36、3.35、2.63 m;采用柔性支护(方案一、二)没有明显改善导硐塑性区的范围;采用刚柔联合支护(方案三)时，塑性区范围得到明显改善，顶板冒落高度、底板和两帮破坏深度分别为1.82、1.63、1.45 m。因此，采用锚网索和工字钢刚柔联合支护方案可以有效控制围岩塑性区范围，保证锚杆、锚索锚固端深入稳定岩层，提高锚固效率。计算所得的塑性区云图如图1所示。

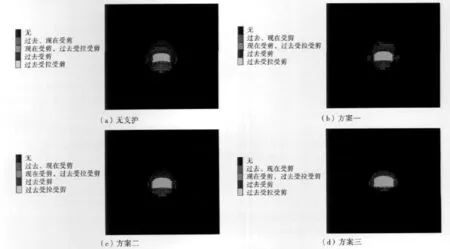
图1 各支护方案塑性区云图

2.2 位移分析

为了确保开切眼工作面的安全与稳定，保证工作面有足够的空间，在数值模拟过程中对导硐顶底板及两帮的最大竖直、水平位移进行监测。结果表明，无支护时，顶底板及两帮的最大竖直、水平位移均较大;采用柔性支护(方案一、二)没有较大幅度减小位移量;采用刚柔联合支护(方案三)时，顶底板及两帮的最大竖直、水平位移分别为38.5、49.3、32.2 mm。因此，采用锚网索和工字钢刚柔联合支护方案可以有效控制顶底板及两帮的竖直和水平位移。监测结果如图2所示。

通过FLAC3D数值软件分别对无支护、柔性支护、刚柔联合支护方案进行计算分析，结果表明，刚柔联合支护方案能够最大限度地控制围岩塑性区的范围和顶底板及两帮的竖直、水平位移，保证工作的安全与稳定。因此，极软弱地层中采用锚网索和型钢支架刚柔联合支护较为合理。

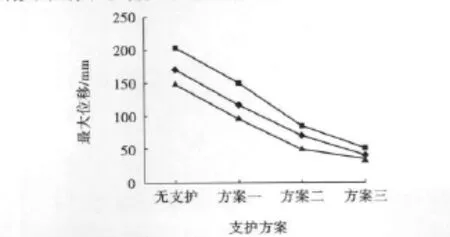
图2 不同支护方案时最大竖直及水平位移

3 支护参数的确定

3.1 锚杆支护参数

(1)锚杆长度。锚杆长度的变化可以改变支护作用范围和支护强度，但过长的锚杆势必要增加很大的工程量和造价，因此有必要对锚杆的长度进行合理计算。按组合梁理论［5］计算，锚杆有效长度取值为2.2 m。采用控制变量方法，固定锚杆直径为20 mm，间排距为700 mm，用FLAC3D数值软件分别对锚杆长度为2.0、2.2、2.4、2.6、2.8 m等5种情况进行模拟，结果表明，当锚杆的长度为2.4～2.8 m时，可以有效地控制顶底板及两帮的最大位移量;考虑到支护成本和锚杆长度与位移的关系，锚杆长度取2.4 m较为合理。锚杆的长度与位移的关系如图3所示。

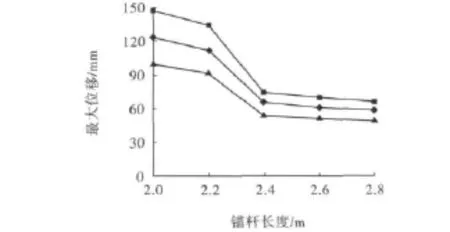
图3 锚杆长度与位移的关系

(2)锚杆直径。为了得到锚杆直径的影响和作用规律，从而选用经济合理的锚杆直径，需要对锚杆的直径进行计算分析。按组合梁理论［5］计算，锚杆直径不小于16 mm，故分别取直径为16、18、20、22、24 mm等5种情形进行模拟。结果表明，当锚杆的直径为20～24 mm时，可以有效地控制顶底板及两帮的最大位移量。考虑到支护成本和锚杆直径与位移的关系，锚杆的直径取20 mm较为合理。锚杆直径与位移的关系如图4所示。

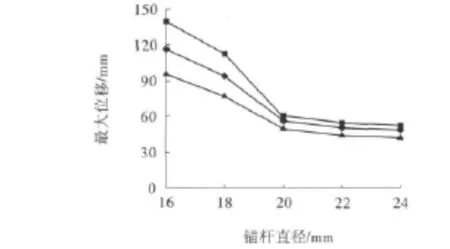
图4 锚杆直径与位移的关系

(3)锚杆间排距。为了得到锚杆间排距的影响和作用规律，从而选用经济合理的锚杆间排距，需要对锚杆的间排距进行计算分析。按照组合梁理论［5］计算，锚杆间排距不大于1 000 mm，故分别对锚杆间排距为600、700、800、900、1 000 mm等5种情况进行模拟。结果表明，当锚杆的间排距为600～700 mm时，可以有效地控制顶底板及两帮的最大位移量。考虑到支护成本和锚杆间排距与位移的关系，锚杆间排距取700 mm较为合理。锚杆的间排距与位移的关系如图5所示。

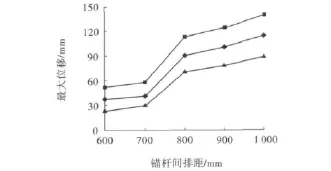
图5 锚杆间排距与位移的关系

3.2 锚索布置方式

为防止顶板因剪切破坏而发生冒顶，应考虑布置在顶板的预应力锚索的可靠性，按照悬吊理论［6］计算得到的锚索的长度和直径为∅17.8 mm×6 000 mm，间排距为1 600 mm×2 100 mm。为了得到锚索不同布置方式下的影响和作用规律，从而选用经济合理的锚索间排距，需要对锚索的布置方式进行计算分析。因此，对锚索采用3－2－3、3－3－3、3－4－3及4－4－4等4种情形进行模拟。结果表明，当锚索采用3－4－3布置时，可以有效地控制顶底板及两帮的最大位移量，因此，锚索采用3－4－3布置较为合理。锚索布置方式与位移的关系如图6所示。

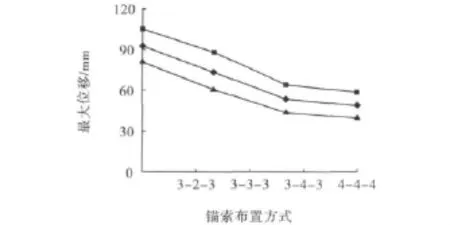
图6 锚索布置方式与位移的关系

3.3 型钢支架承载力的计算

由于工作面开切眼导硐支护方式为锚网索和16#工字钢支架联合支护，单一的锚网索支护系统不能满足结构承载力的要求。因此，在以锚网索支护系统为主要承载结构的基础上对型钢支架进行承载力的计算显得尤为重要。现采用ANSYS数值软件［7-8］对型钢支架进行承载能力的计算。计算时，将拱顶等分为6段，每段长750 mm;边墙等分为4段，每段长800 mm;仰拱等分为6段，每段长750 mm;计算时将40.0%荷载作用在工字钢支架上。计算所得型钢支架的弯矩、轴力分别如图7(a)、7(b)所示。计算结果表明，工字钢支架最危险处出现在顶板，该处弯矩值为25.72 kN·m、轴力为61.38 kN，其他部分内力均较小。

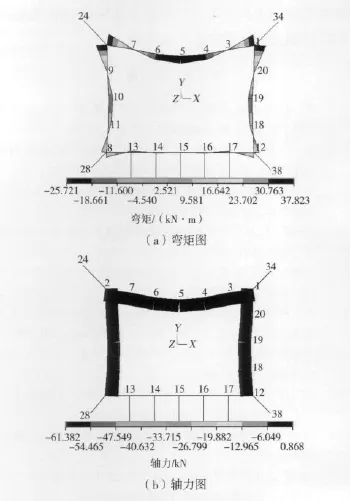
图7 型钢支架内力

16#工字钢支架截面上最大拉应力和压应力［9］分别由式(1)、式(2)计算:

式中，Mmax为最大弯矩，kN·m;Nmax为最大轴力，kN;S为16#工字钢支架截面面积，cm2;Ix为惯性矩，cm4;Wx为抗弯截面系数，cm3。

计算中取值:最大弯矩Mmax为25.72 kN·m，最大轴力为Nmax61.38 kN，16#工字钢支架截面面积为26.1 cm2，惯性矩Ix为1 127 cm4，抗弯截面系数Wx为141 cm3。经计算，最大拉应力σmax=158.90＜215 MPa，最大压应力σmax=205.94＜215 MPa。因此，选用排拒为1 400 mm的16#工字钢支架可以满足承载力的要求。

锚网索和型钢支架刚柔联合支护方案锚杆的参数为∅20 mm×2 400 mm(间排距700 mm)，锚索的参数为∅17.8 mm×6 000 mm(间排距为1 600 mm ×2 100 mm)，型钢支架采用16#工字钢(排距为1 400 mm)。开切眼锚网索和型钢支架刚柔联合支护如图8所示。

图8 刚柔联合支护

4 现场试验效果监测

为了验证锚网索和型钢支架刚柔联合支护方案的可靠性、支护参数的合理性，现场试验段采用“十字布点法”［10-11］在巷道里程11、47、76、112 m处布置4个收敛变形监测断面。监测结果表明，在监测前1周内巷道顶板、两帮收敛变形迅速增长，第2周内收敛变形趋于缓和，3～4周之后，收敛变形趋于稳定。4个监测断面两帮的收敛变形值分别为40、45、42、30 mm，顶板收敛变形值分别为33、26、34、27 mm。巷道顶板、两帮的收敛变形值均不大，和FLAC3D数值计算所得巷道顶板、两帮最大位移分别为38.5、32.2 mm较为一致。因此，锚网索和型钢支架刚柔联合支护方案有效地控制了极软弱岩层中开切眼导硐大变形的特性，可以满足巷道支护结构的承载与稳定性要求。巷道监测断面收敛变形如图9所示。

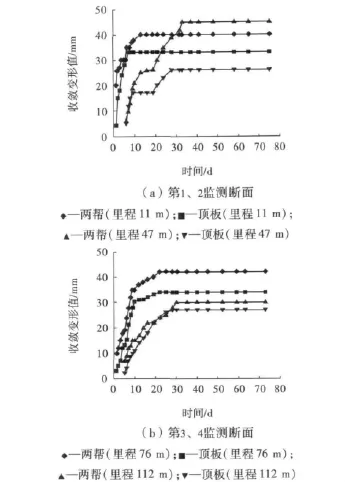
图9 收敛变形监测

5 结论

(1)通过FLAC3D数值软件对无支护、柔性支护、刚柔联合支护方案的计算分析，锚网索和型钢支架刚柔联合支护方案能够最大限度地控制围岩塑性区范围和顶底板、两帮的竖直和水平位移，保证巷道的安全与稳定。

(2)可以通过用理论计算确定锚网索和型钢支架的初始支护参数、用FLAC3D数值软件对锚网索支护参数进行优化、用ANSYS数值软件对型钢支架进行承载力计算的方法确定合理的刚柔联合支护参数。

(3)现场巷道收敛变形监测结果和FLAC3D数值软件计算的结果较为一致。因此，锚网索和型钢支架刚柔联合支护方案可以在蒙东地区极软弱地层开切眼导硐支护实践中推广和应用。

［1］ 徐 磊，桑普天，王凌燕.深部软岩巷道喷、棚、锚、注联合支护技术研究［J］.中国煤炭，2011，37(11):56-58.

［2］ 杨 超，陆士良，姜耀东.支护阻力对不同岩性围岩变形的控制作用［J］.中国矿业大学学报，2000(2):170-173.

［3］ 康红普.煤巷锚杆支护成套技术研究与实践［J］.岩石力学与工程学报，2005，24(21):3959-3964.

［4］ 孙树伟.FLAC3D在岩土工程中的应用［M］.北京:中国水利水电出版社，2011:22-35.

［5］ 夏继宗，韩立军，贾文亮.回采巷道锚网支护参数设计与分析［J］.煤炭工程，2010，10(4):31-33.

［6］ 李 刚，梁 冰，张国华.高应力软岩巷道变形特征及其支护参数设计［J］.采矿与安全工程学报，2009，26(2):183-186.

［7］ 邓凡平.ANSYS10.0有限元分析自学软件［M］.北京:人民邮电出版社，2010:87-98.

［8］ 胡仁喜.ANSYS13.0土木工程有限元分析从入门到精通［M］.北京:机械工业出版社，2011:73-82.

［9］ 夏军武.结构设计原理［M］.徐州:中国矿业大学出版社，2008:65-97.

［10］ 姜耀东.极软岩回采巷道互补控制支护技术研究［J］.岩石力学与工程学报，2009，28(12):2383-2390.

［11］ 孙晓明，杨 军，曹伍富.深部回采巷道锚网索耦合支护时空作用规律研究［J］.岩石力学与工程学报，2007，26(5):895-899.(收稿日期 2012-12-03)