一种新型压电直线电机的建模分析与实验

潘 松，陈培洪，黄卫清

（南京航空航天大学精密驱动研究所，江苏 南京 210016）

0 引言

压电超声电机是20世纪80年代开始发展起来的一种全新概念的微特电机。直线型超声电机具有功率／重量比大、可直接产生直线运动推力、响应快、位置分辨率高和断电自锁等特点，特别适合于小型、精密的直线运动装置的驱动和控制[1-2]。

叠层型压电陶瓷具有输入电压低、变形幅值大、输出力大、响应快、位移可重复性好、体积效率高以及电场控制相对简单等优点[3]。目前，国外早已应用叠层型压电陶瓷制作压电电机[4-6]。叠层型压电陶瓷作为激振元件，定子无需工作在共振状态即可使驱动足产生足够的振幅以驱动动子。同时，由于叠层中的压电陶瓷片很薄，驱动电压也较低，且在低频范围内（小于10kHz），叠层型压电陶瓷的变形幅值达到最大且保持不变[7-8]。应用叠层型压电陶瓷激振的非共振式压电直线电机的工作频率即为输入驱动信号的频率，受温度变化影响小，在一定频率范围内可调。因此，针对基于叠层型压电陶瓷的压电直线电机进行了相关研究。

1 电机工作原理

新型压电直线电机结构如图1所示。定子由定子驱动足、弹性梁、压电陶瓷、楔块、弹性薄梁、驱动足支撑薄梁和定子支座组成，其中定子支座和定子驱动足通过驱动足支撑薄梁连接为一整体结构。如图1所示，压电陶瓷1和压电陶瓷2分别放置在驱动足下端和左端，压电陶瓷1受弹性薄梁支撑，通过楔块1压紧，压电陶瓷2利用弹性梁的作用通过楔块2压紧。

图1 电机定子结构

通过施加在压电陶瓷上2路相位差90°的正弦波激励信号，使压电陶瓷1激发出纵向运动（Z方向），压电陶瓷2激发出横向运动（Y方向），在定子驱动足端部合成椭圆运动，同时通过改变驱动信号（反相时）可实现电机的正反转。

设压电陶瓷1和压电陶瓷2的驱动信号为u1（t）＝A（1＋sin（ωt））和u2（t）＝A（1＋cos（ωt））。陶瓷驱动信号及对应的电机定子驱动足运动过程如图2所示。

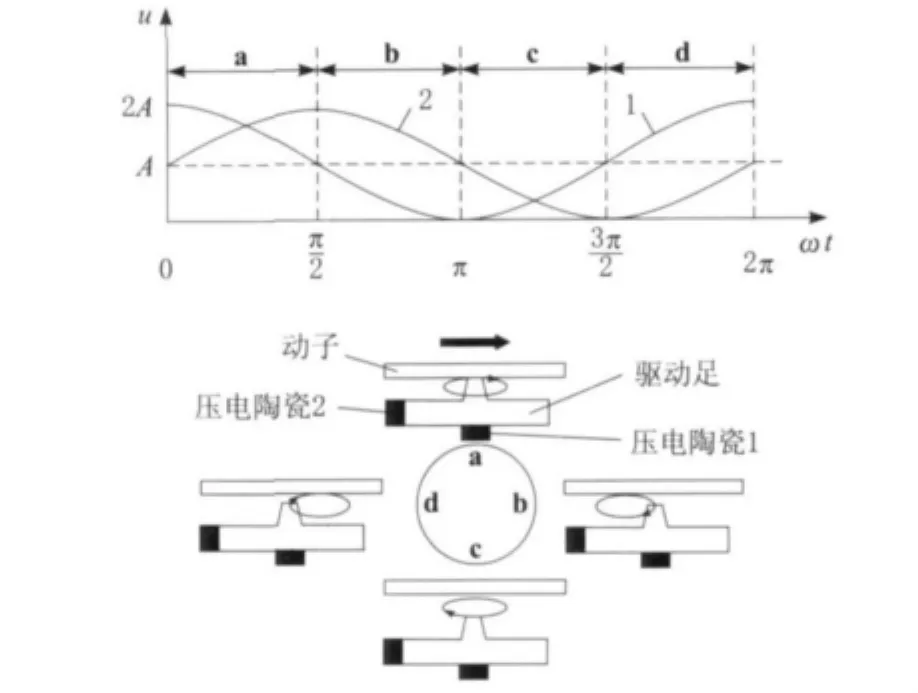
图2 一个周期内驱动足的运动轨迹

压电陶瓷组合成4个状态：

a.纵向振动位移向上达到最大，横向没有位移，驱动足与动子接触。

b.横向振动位移向左达到最大，纵向没有位移，驱动足逐渐与动子脱离。

c.纵向振动位移向下达到最大，横向没有位移，驱动足与动子脱离。

d.横向振动位移向右达到最大，纵向没有位移，驱动足逐渐与动子接触。

电机定子从a到b运动过程中，驱动足逐渐与动子脱离，从d到a运动过程中，驱动足逐渐与动子接触，但这2个过程中定子的振动都驱动动子作直线运动。当振动体的横向振动位移为振幅，即电机处于b或d状态时，电机的输出推力为零[9-10]。

2 电机建模分析

2.1 压电叠堆的输出特性

压电陶瓷利用逆压电效应将电能直接转化成机械能，压电材料的压电应变系数d33数值一般较小。为获得较大的输出力和输出位移，通常将多层压电陶瓷用电学并联、机械串联的方式叠加起来，这能够降低驱动电压并改善力学特性。

在一定的预紧力条件下，压电叠堆能够输出较大的力和位移，且具有承压能力强，提高抗拉和承受剪切能力的特点。因此，压电叠堆作动器应该具有三明治式的结构，即基座、弹性元件和输出机构，如图3所示。其中，基座和输出机构应具有较大的刚度，弹性元件的刚度相对较小。弹性元件的变形可以提供压电叠堆的预紧力。

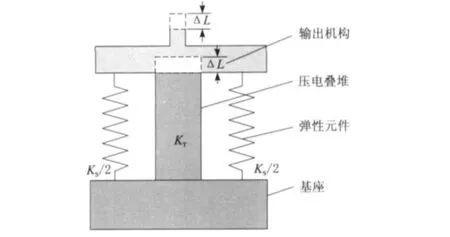
图3 压电叠堆的输出模型

从机械学角度可知，直流电压激励时压电叠堆的输出特性为[11]：

Fmaxeff和ΔL分别为最大有效输出力和最大有效输出位移；ΔL0为无载荷的位移量；KT和KS分别为压电叠堆和外载荷约束的刚度。

由压电学可知，层数为n，压电常数为d33的压电叠堆在直流电压U0激励下，ΔL0近似为：

当正弦电压激励时，在压电叠堆谐振前（低频段），其振动位移的幅值大小与压电陶瓷片的层数、正弦激励电压的幅值成正比，与激励频率无关[12]。

综上所述，忽略压电叠堆的迟滞特性、粘贴层等因素，驱动频率远低于叠堆自身共振频率时，正弦激励电压下压电叠堆的输出特性为：

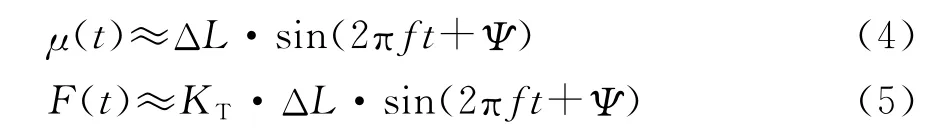
μ（t），F（t）分别为正弦激励下压电叠堆的输出位移函数和输出力函数；f为正弦激励电压频率；Ψ为输出机构响应的相位滞后。

可以把压电叠堆等效成一个电容来分析。事实上多数场合都满足这一条件，压电陶瓷上的电压Uo（t）与电源输出电压Ui（t）满足：

CP为压电作动器的等效电容；r为电源的输出阻抗。

2.2 电机模型分析

为分析电机结构的动力学特性，需要对电机的机械结构进行建模分析。在低频时，2个压电叠堆在垂直和水平方向激起的振动耦合对模型影响不大，所以建模过程中不考虑振动耦合。在机械系统阻尼较小时，如果只是求系统的固有频率或者远离共振区的强迫振动的振幅，那么可以忽略阻尼的作用，但是求系统的共振振幅时，阻尼则不能忽略[13]。系统采用的电机工作于机械结构的非共振区，是强迫振动，建模过程中忽略了结构阻尼。电机动子驱动导轨模型如图4所示。

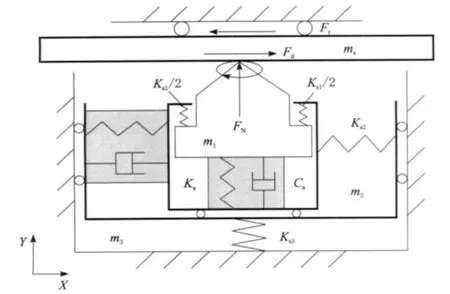
图4 电机模型

纵向作动器的预紧力为Fp1，横向作动器的预紧力为Fp2，定子与导轨之间的预压力为FN，定子与导轨之间的预压力同时也作用在纵向作动器上。根据牛顿运动学定律可以建立系统模型：

m1为驱动足的质量；m2为驱动足和支撑板的质量；m3为定子质量；Ks1为弹性薄梁的刚度；Ks2为弹性梁1和弹性梁2的刚度和；Ks3为定子支撑弹簧的刚度。

驱动足与导轨之间的正压力为FN，导轨与其支架之间的摩擦系数为μ1，导轨与驱动足之间的摩擦系数为μ2，并且有μ2＞μ1，导轨自身质量为ms。驱动足与导轨之间产生的摩擦驱动力为：

导轨运动过程中受到的摩擦阻力为：

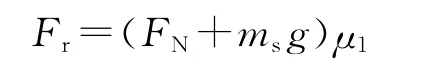
导轨运动方程为：

根据上述模型，以式（6）～式（10）为模型进行计算机仿真分析，可得到各参数对系统动态性能影响特性，为驱动器的结构设计找到理论依据，并指导进行下一步的优化。

在电机设计中，要保证式（7）和式（8）表示的机械振动系统固有频率，远大于式（9）表示的机械系统固有频率。因为m1＜m2＜m3，所以在实际设计中只要设计好刚度Ks1，Ks2和Ks3即可。

3 电机实验研究

3.1 电机的输出特性

基于模型分析设计的电机，在此基础上搭建了实验平台，并进行了一系列实验。

根据设计，电机所需驱动信号的频率低于4 kHz，驱动电压为-20～100V。给压电陶瓷施加所需驱动信号，测得在不同频率下电机速度变化关系，绘制出转子运动速度随频率变化的曲线，如图5所示。

图5 电机速度-频率曲线

由图5可以看出，电机速度与频率成正比关系，随频率的增加而增大，当驱动频率为3.5kHz时，电机最大无负载速度为5mm／s。

电机的机械输出特性曲线如图6所示。可以看出，电机速度随输出推力的增大而减小，电机最大输出推力为5.7N，此时驱动频率为3.5kHz，驱动电压为100V。

图6 电机机械特性曲线

3.2 实验结果分析

由于电机工作在非共振状态，电机驱动足端部的振幅直接由压电陶瓷的振幅决定。分析可知，动子运动速度与驱动足端部垂直方向的振动速度成正比，所以当驱动足振幅不变时，可以认为动子的运动速度与驱动足端部垂直方向的振动频率成正比，即与驱动信号的频率成正比。从图5可以看出，电机在实际运行情况下，转子的运动速度与驱动频率成正比关系。由此可证明，非共振式电机可在一定频率范围内工作且工作频率可调，这与共振式电机只能在定子共振频率附近工作有很大的不同。

根据电机的机械特性输出曲线分析可知，由于电机的输出推力与预压力和摩擦系数大小有关，而摩擦系数的大小取决于定子驱动足和转子材料。这样，在激励电压和频率一定的情况下，施加定子与转子间预压力的大小决定了输出推力的大小。从图6可以看出，电机在不同预压力作用下输出推力与速度的关系，即随着输出推力的增加，速度下降较快。

由以上分析可知，电机实际运行速度较快，当预压力加到一定程度时，虽然转子速度降低了，但电机的输出推力没有增加，反而减小，这可能是由于驱动足振幅比较小及驱动足与转子接触问题造成的。振幅小与压电陶瓷预紧力施加结构有关，而接触问题是由于驱动足与转子接触面摩擦系数较小，驱动足推动转子转动时与转子产生了相对滑动，以及加工误差的影响，驱动足与转子不是理想的面接触，导致受力不均匀。因此，为了提高电机的机械输出特性，需要对压电陶瓷预紧力施加结构，以及电机的定转子所用摩擦材料和定转子接触模型进行深入研究。

4 结束语

分析了一种新型基于叠层型压电陶瓷压电直线电机的运行机理，并在此基础上进行了建模分析。基于建模分析对电机的结构设计进行了优化，并对所设计的电机实物进行了相关实验。通过实验发现电机可在300Hz～4kHz范围内工作，其运行速度与工作频率成正比。电机最大无负载速度为6 mm／s，最大输出推力为5.7N。与模型仿真预测结果相近。

[1]赵淳生.超声电机技术与应用[M].北京：科学出版社，2007.

[2]许 海，赵淳生.直线型超声电机的发展及应用[J].中国机械工程，2003，14（8）：715-717.

[3]温建明.新型惯性压电叠堆驱动机构的研究[D].吉林：吉林大学，2006.

[4]Kim J，Lee J H.Self-moving cell linear motor using piezoelectric stack actuators[J].Smart Materials ＆Structures，14（5）：934-940，2005.

[5]Salisbury S P，Waechter D F，et al.Design considerations for complementary inchworm actuators[J].IEEE／ASME Transactions on Mechatronics，2006，11（3）：265-272.

[6]Salisbury S P，Waechter D F，et al.Closed-loop control of a complementary clamp piezoworm actuator[M].IEEE／ASME Transactions on Mechatronics，2007，12（6）：590-598.

[7]李国荣，陈大任，殷庆瑞.PZT系多层片式压电陶瓷微驱动器位移性能研究[J].无机材料学报，1999，14（3）：418-424.

[8]李艳林，黄卫清.一种低频大行程直线型压电电机的研究[J].压电与声光，2009，31（4）：507-509.

[9]苏艳文，黄卫清.一种基于矩形薄板面内振动的新型直线超声电机[A].第十一届中国小电机技术研讨会论文集[C].上海：中国电子元件行业协会微特电机与组件分会，2006.217-221.

[10]黄卫清，孟益民.一种新型非共振压电直线电机的设计[J].中国机械工程，2009，20（14）：1717-1721.

[11]刘建芳.压电步进精密驱动器理论及实验研究[D].长春：吉林大学，2005.

[12]陶继增，王中宇，李 程.压电叠堆在正弦电压激励下振动位移特性的研究[J].计测技术，2006，26（6）：20-22.

[13]邹慧君，傅祥志，张春林，等.机械原理[M].北京：高等教育出版社，1999.