基于WD-LSSVM的监护信息预报研究

蒋贤海，谢存禧

（1.广东水利电力职业技术学院 机械工程系，广东 广州 501635；2.华南理工大学 机械与汽车工程学院，广东 广州 510640）

0 引言

生理参数是一弱非平稳的时间序列，基于统计理论的预报方法虽然在数值预报中发挥了重要作用，但它们都是建立在线性相关基础上的[1,2]，在实际应用中存在一定的局限性。具有非线性能力的神经网络也取得较大进展[3,4]，然后由于神经网络的过学习问题，所得到的值往往是局部最优，预报效果不够理想。随着计算机技术的发展和智能技术的进步，智能机器识别技能得到很好的发展。支持向量机（SVM）[5]是一种新的小样本机器学习方法，具有从海量信息中自动识别并提取关键信息，它借助于最优化方法来解决机器学习问题。已成为克服维数灾难和过学习等传统问题的有力手段，适用于处理本质上的非线性问题。

针对生理信号预报问题，本章提出小波分解与最小二乘支持向量机（WD-LSSVM）的综合预报方法。利用小波分解将原参数序列分解为逼近信号和细节信号，然后采用LS-SVM算法，分别建立逼近信号和细节信号的预报模型，得到逼近信号和细节信号的预报值，最后将各部分预报值利用小波逆变换进而得到最终预报结果，并推广到生理参数时间序列的N步预报。可直接对N步预报值进行异常判断，无需等到N步实际值出现就可实现状态预报。

1 基于WD-LSSVM的监护信息预报方法

本文研究的监护信息是典型的时间序列数据。时间序列是按时间顺序产生和排列的，随时间变化且相互关联的观察数据序列[6，7]。时间序列分析主要对时间序列建立预报模型，并根据变量本身的变化规律来预报未来的变化，描述如下。

设一时间序列{x（1），x（2），…，x（N）}，时间序列预报就是根据时间序列的历史数据{x（t），x（t-1），…，x（t-m+1）}预报未来t+k时刻值x（t+k），即寻找x（t+k）与历史数据{x（t），x（t-1），…，x（t-m+1）}间的关系。当k=1时，为一步预报；当k＞1时，为多步预报。m参数为嵌入维数。

预报是利用各个时刻监护数据，将时间作为自变量，监护数据作为因变量，通过回归分析，建立监护信息与时间的函数关系，用此模型函数作为进行未来生理参数数据的预报根据。由于现有监护信息预报方法存在的不足，本文根据小波分解特点及支持向量机具有小样本、非线性、高维数、避免局部最小点以及过学习现象等优点，以及最小二乘支持向量机用等式约束代替了不等式约束，其算法可转化为解线性方程组，比标准支持向量机法待选的参数少，不再需要指定收敛判据的精度，具有运行简单、求解速度快、精度高的优点，采用小波分解与最小二乘支持向量回归相结合的方法，构造一小波分解与PSO[8]优化LSSVM监护信号预报数学模型逼近真实的监护信号，然后用这一模型对监护信号进行预报。

2 基于WD-LSSVM的监护信息预报模型

基于小波分解与PSO优化LS-SVM的监护信息预报算法流程如图1所示。基本思路是通过小波分解将原参数序列分解为逼近信号和细节信号，然后采用PSO优化的LS-SVM算法，分别建立逼近信号和细节信号的预报模型，得到逼近信号和细节信号的预报值，即和（i=1，2，…，j），最后将各部分预报值利用小波逆变换进而得到最终预报结果，即：

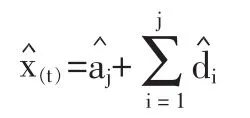
流程描述如下：

（1）监护数据归一化。在进行建模预报前，首先要对监护数据进行归一化处理，以减少训练过程中数值计算的复杂度。

式中xi—样本数据；xmax和xmin分别为样本数据中的最大值和最小值；xi'—归一化后的数据。

（2）监护数据小波分解。对归一化后的监护数据序列进行小波分解，得到各层分解序列。

（3）构建训练样本。对经小波分解的各层数据，分别构建训练样本。当训练回归模型时，样本对可以表示为：输入向量{x（t），x（t-1），…，x（t-m+1）}，对应的输出值为x（t+1），输入向量{x（t+1），x（t），…，x（t-m+2）}，对应的输出值为x（t+2），并依此类推，由n个训练样本就可以构建n-m个训练样本对。假定第i层数据序列的前n个数据用于模型的建立，其余N-n个数据用于验证所建立模型，下面的矩阵作为预报模型的输入输出（xi，yi）（i= 1,2,…,n）：

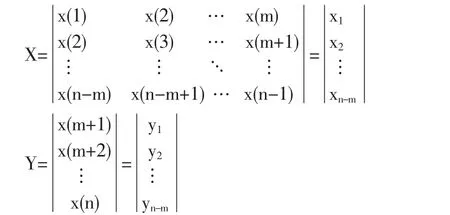
（4）计算LS-SVM预报模型参数。

（5）用（3）建立的训练样本和（4）优化参数对模型进行训练。即找出输入X和输出Y间的函数f，使得yi=f（xi）（i=1,2,…,n）。

（6）用训练好的预报模型，对小波分解的各层数据进行预报。

（7）对各层的预报结果进行小波逆变换。

（8）数据反归一化。最后对预报模型的输出数据进行反归一操作，以恢复数据为监护数据实际预报值。xi=xi'（xmax-xmin）+xmin。

3 实验

（1）实验数据。实验数据采用PhysiNet生物医学信号研究资源中的数据，PhysiNet是一个基于web的复杂生理参数和生物医学研究资源[9]。实验中使用心率生理参数数据集合。心率数据取自于Santa Fe Time Series Competition数据库。以上实验数据均由Boston Beth Israel医院的睡眠实验室对监护对象在睡眠状态下进行连续监测获得。下面将分别采用小波分解与最小二乘支持向量回归法，直接采用最小二乘支持向量回归法和BP神经网络对上数据集进行训练和预报，以验证本预报方法的有效性。

（2）实验步骤：①选择好训练样本及测试样本后，采用db6小波基对训练样本进行3层小波分解；②对小波分解后的低频序列和高频序列分别进行基于PSO的LSSVM预报；③最后，合成各分解序列的预报结果，并对合成的第3层低频系数及第1～3层高频系数分别进行小波重构，得到最终的预报结果。

（3）实验结果：本文选择径向基函数作为监护信息预报模型的核函数。选择100个心率样本，前80个作为训练样本，后20个作为预测样本，分别采用最小二乘支持向量机、BP神经网络及小波分解与最小二乘支持向量机方法进行预报，实验结果如下。图2～4是分别采用LS-SVM、神经网络及WD-LSSVM对心率信号预报结果。三种预报方法的心率预报误差如图5所示。

为了对实验做进一步说明，引入均方差对实验结果进行定量分析。不同方法预报均方差结果见表1（其中经PSO得到的参数为gam=790.6295，sig2=3.736199）。

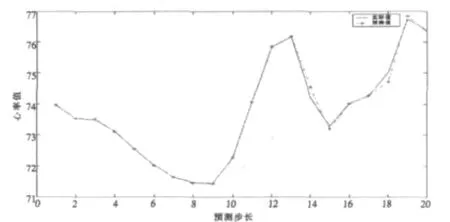
图2 心率LS-SVM预报结果

图3 心率神经网络预报结果

图4 心率WD与LS-SVM综合法预报结果

图5 心率预报误差曲线

（4）实验结果分析。从表1可得出，最小二乘支持向量机预报方法较神经网络预报好，原因是最小二乘支持向量机较神经网络的推广能力强，善于从小样本中学习，既考虑经验风险最小又考虑泛化能力最大，从中找到一平衡点，所以预报效果优于神经网络。而本文提出的小波分解与最小二乘支持向量机综合预报方法明显优于其他方法，是因为本文方法对经小波分解的监护信息各层信号进行预报，然后再将各层预报结果进行小波逆变换得到最终预报结果，效果显然优于对监护信号直接采用最小二乘支持向量机预报方法。实验结果说明小波分解与最小二乘支持向量机预报方法更适合对监护信息的预报。

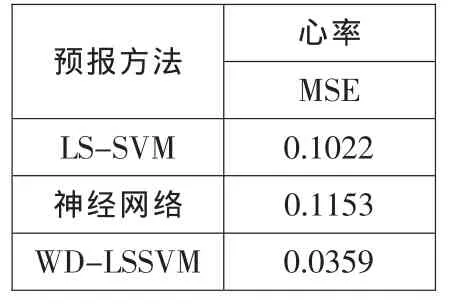
表1 心率信号不同预报方法均方差

4 结束语

本文提出了小波分解与最小二乘支持向量机的监护信息预报方法，建立监护信息小波分解、重构模型及监护信息各层分解信息LS-SVM模型。给出了监护信息预报方法流程。对美国MITBIH标准数据库中的心率信号数据进行了仿真验证，并分别与最小二乘支持向量机方法、小波神经网络方法进行了比较，得出本文方法预报的均方根误差分别为0.0359。明显优于其他方法，验证了本文提出的监护信息预报方法的有效性。

[1]Vapnik V.N.An overview of statistical learning theory[J].IEEE Trans Neural Network,1999，5.

[2]Christensen,R.and Pearson,L.M.Prediction diagnostics for spatial linear models.Biometrika.1992，79.

[3]Zhang Zhengdao,Hu Shousong.Fault prediction of fighter based on nonparametric density estimation[J].Journal of Systems Engineering and Electronics, 2005，4.

[4]Xu K,Xie M,etc.Application of Neural Networks in forecasting Engine Systems Reliability[J],Applied Soft Computing.2003,2.

[5]HANBAY D.An expert system based on least square support vector machines for diagnosis of the valvular heart disease[J].Expert Systems with Applications，2008.

[6]Box and Jenkins；顾岚，范金城（译）.时间序列分析预测与控制[M].中国统计出版社，2003.

[7]Policker S,Geva A.B.A New Algorithm for Time Series Prediction by Temporal Fuzzy Clustering[A].Proceedings of 15th International Conference on Pattern Recognition[C],ICPR.2000.

[8]邵信光，杨慧中，陈刚.基于粒子群优化算法的支持向量机参数选择及其应用[J].控制理论与应用，2006，5.

[9]Moody G B,Mark R G,Goldberger A L.PhysioNet:a web-based resource for the study of physiologic signals[J].IEEE Engineering in Medicine and Biology Society，2001，3.

[10]何仁斌.MATLAB6工程计算及应用[M].重庆大学出版社，2001.