低复杂度串行级联LDGM码构造方案

多 滨，王振永，顾学迈

(哈尔滨工业大学 通信技术研究所，150080 哈尔滨)

近年来，随着信息理论应用的快速发展，Turbo码和 LDPC(Low Density Parity Check，LDPC)码都被看作是信道编码领域中两类具有逼近 Shannon理论限的信道编码方案［1－2］.但是这两种编码的编码或译码复杂度较高，在实现过程中还需进一步优化.在实际应用中，编译码方案复杂度的问题是需要考虑的一个关键问题，因此寻找一个编码复杂度和译码复杂度同时较低，并且具有应用性能优异的码字是信道编码领域研究的一个重点.

作为一类特殊的 LDPC码，LDGM(Low Density Generator Matrix，LDGM)码有编码复杂度和译码复杂度都低，并且实现更为简单的优点［3］，因此，研究具有低编译码复杂度的 LDGM码的信道编码技术方案具有重要的理论和实用价值.LDGM码是线性系统码，其校验矩阵可以通过一个随机构造的稀疏矩阵与单位矩阵简单的组合得到，因此可以看出LDGM码的构造主要与该稀疏矩阵的如何创建有关.虽然稀疏矩阵的产生与LDPC码校验矩阵的生成类似，但是目前还没有一个统一确定的产生方法，因此，自从MacKay［4］等重新发现LDPC码的优异性能以来，在校验矩阵的构造方面始终是一个研究热点.由于LDGM码校验矩阵的稀疏性，它同样可以采用适用于LDPC码的置信传播(Belief Propagation，BP)算法，而不改变其译码复杂度.尽管LDGM码有如此多的优点，但由于存在度为1的变量节点，LDGM码译码性能存在较高的错误平层.文献［3］提出了串行级联低密度生成矩阵(Serially-Concatenated LDGM，SCLDGM)码，其不仅可以明显地改善LDGM码译码中所存在的错误平层现象，还能获得逼近Shannon理论限的优异性能.目前，针对SCLDGM码的研究主要集中在如何进一步降低或消除LDGM码的高错误平层的问题［5－7］.然而，对于如何具体产生适合 SCLDGM码的编码构造并没有被提及.

为此，本文从实际应用的角度出发，首先在保证性能的前提下，提出了一种具有低复杂度的LDGM码编码构造算法.此外，为了进一步提高译码性能，结合SCLDGM码的逼近Shannon理论限的特点以及拥有着很好的错误平层性能的优点，给出了一种改进的级联译码算法.该算法是将外编码器的输出和内译码器的输出看作二进制删除信道(Binary Erasure Channel，BEC)，因此将该信道的先验信息输入外译码器，可以进一步降低错误信息.通过计算机仿真，验证了不同仿真参数下的性能差异，找到了提出方案近优的内外码速率组合和近优的内外码码重.仿真结果表明，本文提出的算法不仅具有较低的复杂度，同时有效的降低了LDGM码错误平层.

1 LDGM码编码构造

在本节中，分析了LDGM码基本原理，提出了具有低复杂度的稀疏矩阵构造算法，该算法对于本文第2节提出的SCLDGM编译码方案起着至关重要的作用.

1.1 LDGM码校验矩阵构造

LDGM码是一类特殊的LDPC码，正如式(1)所示，一个系统 LDGM码的校验矩阵包括左右两个部分:左侧是一个随机构造的稀疏矩阵P，右侧是一个对角单位矩阵I.如果P中所有的行(和列)都有同样数量“1”，那么该LDGM码就被称为规则LDGM码;如果P中所有的行(和列)中“1”的数量不一样，则把其称为非规则LDGM码.

式中，校验矩阵H有N列和M行，那么N个比特的码字序列c必须满足校验关系HcT=0.信息比特的数量为K=N－M，编码速率为R=K/N.本文用(N，K，w)分别表示非规则LDGM码的编码长度、信息比特长度和码重.

当系统信息比特、校验比特和码字序列分别表示为 u= ［uk］T、p= ［pm］T和 c= ［cn］T=［u1… ukp1… pm］T时，LDGM 码的编码可以由下式表示:

式中 hm，n表示矩阵中第 m列、第 n行元素在校验矩阵中相应的位置.需要注意的是，LDGM码是一类特殊的LDPC码，因此其译码方式同样可以采用适用于LDPC码的BP算法，只需对其译码算法进行适当的改变，而不增加其译码复杂度.

与LDPC码相比，LDGM码唯一不同之处就是存在N－K个度为1的校验比特节点和K个比特节点对应着系统信息比特.因此，LDGM码无法更新来自度为1的比特节点到相应校验节点的对数似然比(Log Likelihood Ratio，LLR)软信息，所以LDGM码的缺点就是存在较高的错误平层问题.虽然可以在LDGM码的性能收敛性和性能错误平层性之间采取一个折中的方案，但是单独利用LDGM码作为信道编码方案在实际无线信道应用中还有一定的局限性.

1.2 低复杂度稀疏矩阵构造算法

由上述可知，LDGM码的构造是由稀疏矩阵的构造决定的.而LDPC码的性能好坏完全由它的校验矩阵来确定，也就是说校验矩阵的构造对于LDPC码的性能起着决定性的作用.现有的LDPC码校验矩阵的随机构造方法主要有Gallager构造法［8］和 Mackay 构造法［4］.其中，为了避免Tanner图中长度为4的短环，Mackay的1A构造法保证每列有t个“1”，并随机设定它们的位置，使每一行中的“1”尽可能相等均匀分布，同时任意每两列之间的重叠“1”的个数不大于1.Mackay的1A构造方法不仅保证了矩阵的随机性，同时通过相关算法(由于篇幅限制，该算法请参考文献［4］)进一步消除了长度为4的短环.

虽然采用Mackay方法构造的稀疏矩阵具有很好的码距离特性，同时避免了长度为4的短环，但缺点是稀疏矩阵的构造复杂度较高，而且所构造的稀疏矩阵有50%的概率存在线性相关的行，使得实际的码率略有增加［4］.本文定义采用Mackay方法构造的LDGM码为LDGM1码.

为了解决LDGM1码复杂度较高的问题，本文提出一种具有低复杂度的不规则稀疏矩阵构造方法，具体算法步骤如下:

1)稀疏矩阵初始化:生成维度为(N－K，K)的全0矩阵作为初始稀疏矩阵.随机分配给定列重数量的每一个“1”到初始化的稀疏矩阵的每一列当中，完成稀疏矩阵的初始化;

2)检验与更新稀疏矩阵:经过初始化生成的矩阵中任意同一列中可能会存在相同行位置的“1”的分配，所以，还需要对初始化的稀疏矩阵进行逐列检测，如果发现同一列中有相同的行位置分配，则对该列“1”的位置进行重新随机分配，直到该列没有相同的行位置分配，最后更新稀疏矩阵;

3)生成LDGM校验矩阵和生成矩阵:将得到的稀疏矩阵与单位矩阵组合即可以生成相应的生成矩阵与校验矩阵，分别用于LDGM码的编码与译码.定义用此构造法构造的LDGM码为LDGM2码.

与LDGM1码的稀疏矩阵相比，LDGM2码并没有消除长度为4的短环，故不需像LDGM1码那样反复验证构成稀疏矩阵是否存在长度为4的短环，所以LDGM2码的生成具有较小的计算量，即复杂度相对较低.图1给出了 LDGM1码和LDGM2码的BER性能比较.为了公平比较均选取编码长度为1 000，列重为6和码速率为0.5的LDGM码.从图中可以看出，尽管LDGM1码的P矩阵消除了长度为4的短环，但是不能保证H矩阵也不存在长度为4的短环，因此与LDGM2码相比，LDGM1码的性能并没有大幅度的增益，其性能仅仅略高于LDGM2码的性能.同时随着码长的不断增加，构建LDGM1码中P矩阵的计算时间将越来越长，所以其对于长码字的应用存在一定的局限性.而本文提出的算法尽管性能上有很小的损失，但是随着编码长度的不断增加，其性能也会不断提高，并且其较低的编码复杂度使其在实际应用当中具有很好的应用前景.

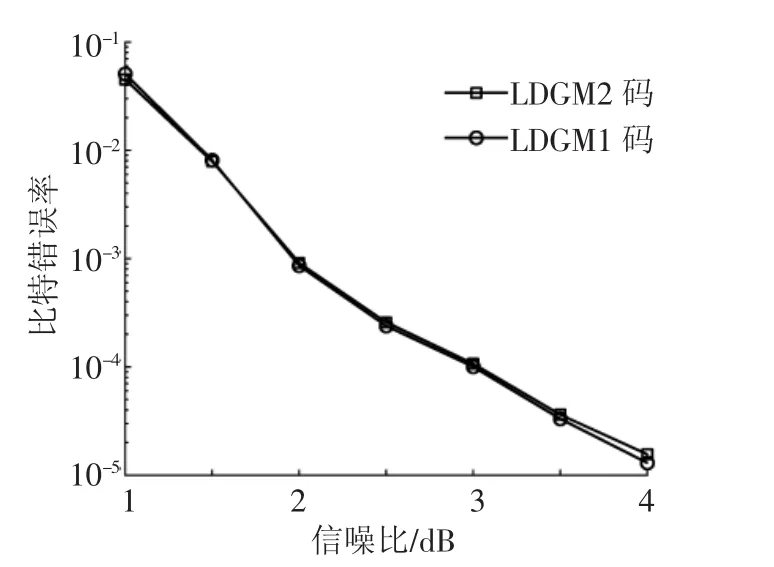
图1 (1 000，500，6)的LDGM1码和LDGM2码性能比较

2 SCLDGM码编译码设计方案

2.1 SCLDGM码编译码构造

图2给出了SCLDGM码编译码系统框图，可以看出，该系统是将二进制LDGM码分别作为系统的内码和外码进行串行级联的.具体来说，首先用高码率为K/N1的外LDGM码编码器对待发送信息进行编码，然后对外编码器的输出码字用码率为N1/N的内LDGM码编码器再次编码，最后生成总码率为K/N的码字.码字经过BPSK调制后，通过高斯随机变量方差为 σ2=N0/2的AWGN信道.在信宿端，内译码器首先利用校验矩阵对接收到的信号进行译码.直到内译码器译码完成后，外译码器才利用内译码器输出的LLR软信息作为先验信息对外译码器的输入进行初始化.待外译码器译码完成后，即可得到信源发送信息的估计值.

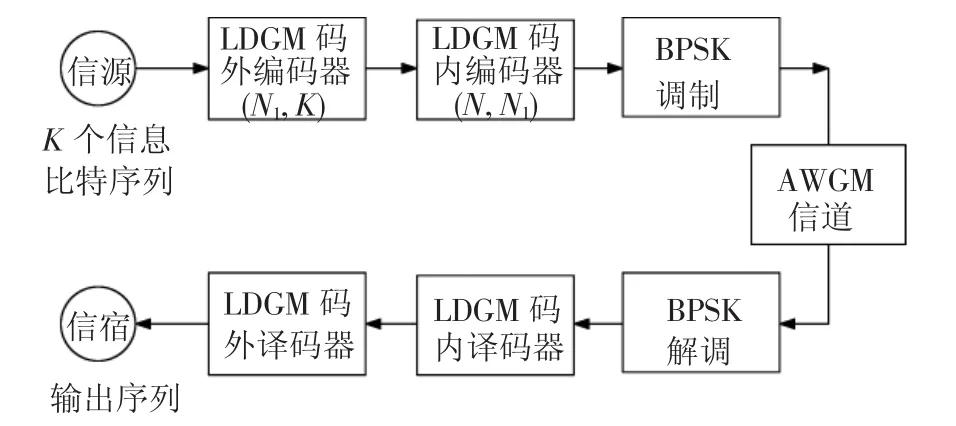
图2 SCLDGM码编译码系统框图

2.2 SCLDGM码译码算法

1)级联译码算法1.对于SCLDGM码译码，传统的方法采用内外码LLR软信息单独迭代传递方案.首先，从AWGN信道接收到的信号经过BPSK解调后送入到内LDGM码译码器，采用BP迭代译码算法在内译码器中的变量节点和校验节点之间进行若干次LLR软信息迭代更新后，从变量节点得到最后的LLR软信息，即对应内译码器的译码输出信息.将内译码器的输出LLR软信息作为外译码器的先验概率软信息进行初始化输入.然后外译码器进行若干次BP迭代译码得到最后的LLR软信息，即外译码器的输出软信息，最后通过判决得到译码结果.

2)级联译码算法2.本文在级联译码算法1的基础上提出一种改进的级联译码算法，称之为级联译码算法2.从级联译码算法1可知，LDGM外译码器可以利用内译码器的输出作为先验信息进一步降低内译码器的译码错误比特，所以，内译码器的输出实际上已经含有输出错误比特位置信息.因为通过仿真发现，内译码器输出的正确译码比特0或者1的概率接近于1，即内译码器对该比特正确译码的确定性为100%;而相比之下，内译码器输出的错误比特0或者1的概率接近于0.5，即内译码器对该信息比特的判定是0或者1的确定性为50%.这就意味着可以把图2当中从外编码器的输出到内译码器的输出部分看成是BEC信道，而内译码器输出的错误系统信息比特就相当于BEC当中已经被“删除”的比特.需要注意的是，这个BEC信道并不是一个标准的BEC信道，因为并不知道错误信息比特确切的位置，但是内译码器的输出信息却含有错误信息比特的先验概率信息.外译码器可以将内译码器的输出看作是来自BEC信道的输出信号，然后利用内译码器输出信息比特的先验概率信息得到被“删除”比特位置的先验信息，这些比特的初始化LLR软信息为0.最后完成所有比特先验概率初始化，输入到外译码器当中，使得外译码器可以进一步准确的完成对来自内译码器的先验概率信息的译码.

3 仿真分析与结果

本小节，通过计算机对无线通信信道中的环境进行模拟仿真构造近优的SCLDGM码方案.因此数据传输速率选择不能太高，为了便于仿真验证本文提出的构造SCLDGM码方案的可行性，首先考虑近优的内外码速率组合，并假设整个SCLDGM码码率R为0.5，那么内外码速率的乘积为0.5;其次，分析内外码码重对级联方案性能的影响.

1)确定近优内外码速率组合.定义内外码码率分别为Rin和Rout，那么R=Rin×Rout=0.5.首先要找到一种近优的内外码速率组合以达到最好的BER性能.需要注意，Rin和Rout都大于码速率0.5.由于高码率的LDGM码拥有优异的BER性能(不仅距离Shannon理论限仅有0.36 dB，同时还保持着非常低的错误平层［9］)，所以图2中的外译码器可以利用内译码器的输出作为先验概率信息来进行初始化操作，然后通过高速率的外译码器进一步降低内码译码没有消除的错误.因此为了使得外码速率的损失最小，选择Rin接近于R，那么Rout则接近于1.作为所有内外码速率组合采样的代表，图3给出了3种不同内外码速率组合的 BER性能曲线.内外码速率组合(Rin，Rout)分别为(0.990 1，0.505)、(0.980 4，0.51)和(0.970 9，0.515).从图中可以看出，最优的速率组合是(0.980 4，0.51).

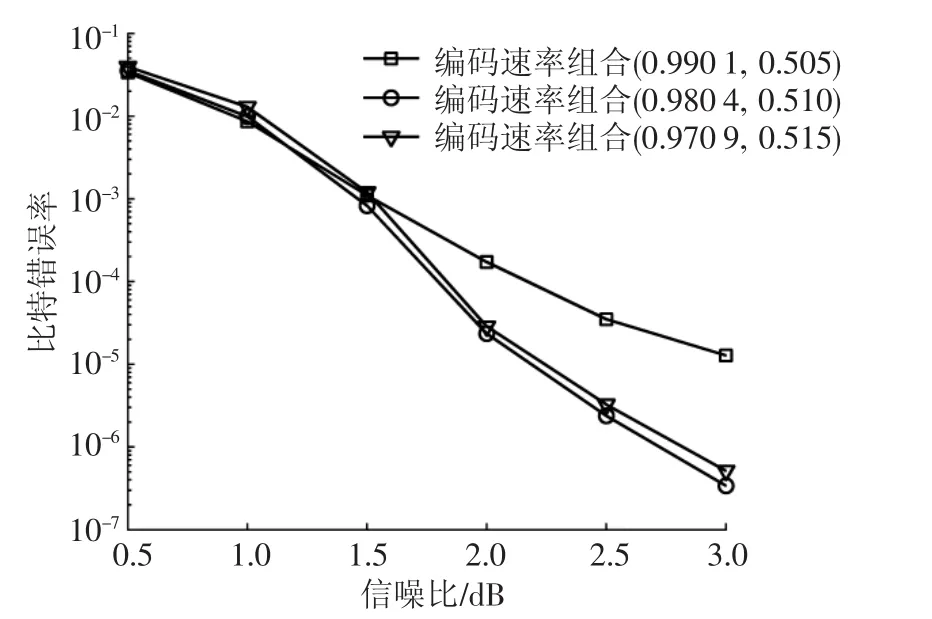
图3 具有不同内外码速率组合的SCLDGM码的BER性能

2)确定近优内外码码重.为了便于仿真分析内外码码列重的选取是否也会对SCLDGM码方案的性能产生一定的影响.作为所有内外码码列重组合采样的代表，假设其内外码码重具有相同的数值 D.图 4给出了 (600，500，wout)外LDGM码和(1 176，600，win)内LDGM码3种不同内外码码列重组合级联方案的BER性能曲线，其中wout和win分别为外码和内码的列重.从图中可以看出，SCLDGM码存在近优的内外码码重，且近优的内外码码重D为6.

图4 级联(600，500，wout)外 LDGM 码和(1000，600，win)内LDGM码的BER性能

3)性能比较与分析.图5分别比较了码长为1 176、码率为 0.5的传统 LDGM码、具有Mackay构造法的SCLDGM码和具有本文提出构造法的SCLDGM码的BER性能，并且对级联译码算法1和级联译码算法2做出了性能比较.从图中可以看出，近优SCLDGM码方案可以极大的改善LDGM码错误平层问题，这是因为经过内译码器后剩余的错误比特可以被外译码器进一步纠正.同时，级联译码算法2在级联译码算法1的基础上，其性能得了到进一步的改善.

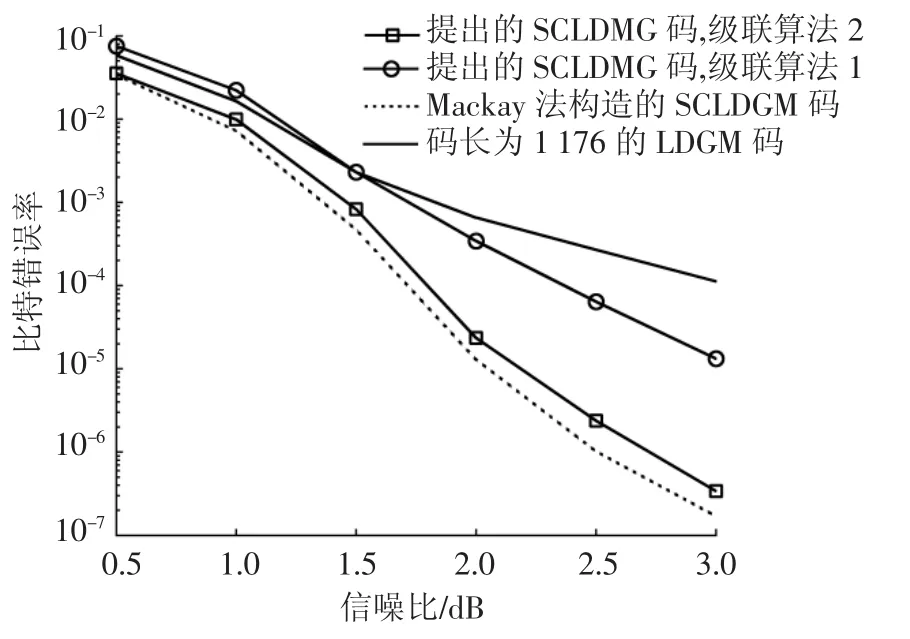
图5 LDGM码和SCLDGM码的不同译码算法BER性能比较

如图5所示，对于采用Mackay的1A构造法的SCLDGM码虽然在性能上略优于本文提出的SCLDGM码，但是随着编码长度的不断增加，与第2.2小节分析结果类似，通过仿真得到，Mackay构造法的复杂度也将会越来越高，优势也相应的越来越小，所以对于长码字的应用存在一定的局限性.而本文提出的算法尽管在性能上略低于Mackay构造法，但是其较低的编码复杂度，以及编码的快速性，使其在实际应用当中具有很好的应用前景.

4 结论

本文针对SCLDGM码稀疏矩阵构造复杂度较高的问题，提出了一种具有低复杂度的SCLDGM码编码设计方案.首先，给出了低构造复杂度的LDGM2码生成算法，仿真表明，与LDGM1码相比，LDGM2码仅有很小的性能损失.此外，通过计算机仿真确定了仿真参数，分别为近优的内外码码率组合以及内外码码重.仿真结果表明，本文提出的SCLDGM码编译码算法可以有效克服LDGM码所存在的错误平层问题，在保持其实现低复杂度和编码快速性的同时可以大幅改善传统LDGM码性能.

综上，本文提出的低复杂度SCLDGM码构造方法在无线通信信道当中具有相当好的BER性能，随着编码长度的不断增加，其性能将会接近于随机构造的非规则LDPC码，因此，在无线通信中具有良好的应用前景.由于本文提出的方案是近优的，下一步工作将利用EXIT图［10］进行理论分析，设计最优的SCLDMG码方案，以期进一步提高系统的性能.

［1］ ZHANG Zheng，DUMAN T M.Capacity approaching turbo coding forhalfduplexrelaying［C］//IEEE International Symposium on Information Theory.Piscatway:IEEE Press，2005:1888 －1892.

［2］CHAKRABARTI A，SABHARWAL A，AAZHANG B.Low density parity check codes for the relay channel［J］. IEEE Journal on Selected Areas in Communications，2007，25(2):280 －291.

［3］GARCIA-FRIAS J，ZHONG Wei.Approaching shannon performance by iterative decoding of linear codes with low-density generator matrix［J］.IEEE Communications Letters，2003，7(6):266－268.

［4］ MACKAY D C.Good error-correcting codes based on very sparse matrices［J］. IEEE Transactionson Information Theory，1999，45(2):399 －431.

［5］GONZALEZ-LOPEZ M，VAZQUEZ-ARAUJO F J，CASTEDO L，et al.Serially-concatenated low-density generator matrix(SCLDGM)codes for transmission over AWGN and Rayleigh fading channels［J］.IEEE Transactions on Wireless Communications，2007，6(8):2753 －2758.

［6］ ZHONG Wei，GARCIA-FRIAS J.LDGM codes for channel coding and joint source-channel coding of correlated sources［J］.EURASIP Journal Applied Signal Process，2005，6:942 －953.

［7］VAZQUEZ-ARAUJO F J，GONZALEZ-LOPEZ M，CASTEDO L，et al.Serially-concatenated LDGM codes for MIMO channels［J］. IEEE Transactions on Wireless Communications，2007，6(8):2860－2871.

［8］GALLAGER R G.Low density parity check codes［J］.IEEE Transactions on Information Theory，1962，8:21－28.

［9］VAZQUEZ-ARAUJO F，GONZALEZ-LOPEZ M，CASTEDO L，et al.Layered LDGM codes:a capacity-approaching structure for arbitrary rates［C］//4th International Symposium on Wireless Communications Systems.Piscatway:IEEE Press，2007:16 －20.

［10］TEN BRINK S，KRAMER G，ASHIKHMIN A.Design of low-density parity-check codes for modulation and detection［J］.IEEE Transactions on Communications，2004，52(4):670－678.