基于时域平滑FFT累加算法的循环谱实现方法

宋鹏，张麟兮，张曼，唐勇

（1.西北工业大学电子信息学院，陕西西安710129；2.湖北省京山县第一高级中学湖北荆门431800）

无人机数据链所采用的通信信号都是有调制的信号，调制信号的解调多数情况下需要恢复载波信息，载波恢复性能对信号解调有着很大的影响。当信号的信噪比较低时，一般用于载波提取的锁相环性能严重下降或失锁，通常以环路信噪比6 dB作为环路的失锁门限[1]。为了在低信噪比条件下，保证无人机顺利的完成预定任务，有效载波频率提取成为无人机数据链的关键技术之一。

自上世纪80年代，Gardner.W.A.等人提出了循环谱[2-3]这一概念后，循环平稳信号处理技术已在通信、雷达、声纳等信号处理方面得到了广泛的应用，如：扩频通信信号的检测与识别，雷达信号检测与参数估计以及阵列信号处理等领域。循环谱密度函数将通常的功率谱定义域从频率轴推广到了频谱频率——循环频率双频率平面，且对于平稳噪声而言，在非零循环频率处循环谱密度函数为零，即在非零循环频率处不呈现谱相关。因此，本文使用循环谱技术，可以有效的摆脱平稳噪声对参数估计的影响，实现低信噪比条件下，对信号的载频估计。

1 循环谱相关理论

1.1 循环自相关函数

通常把统计特性呈周期或多周期平稳变化的信号称为循环平稳或周期平稳信号。设x（t）为循环平稳信号，T为循环周期，循环自相关函数（τ）可以表示为[3]：

其中，τ为时间间隔。我们把Rαx（τ）≠0的频率α称为信号x（t）的循环频率。从式（1）可以看出，循环自相关函数实际是在不同循环频率上，对输入信号的相关函数乘上不同的循环系数e-j2παt，使得信号的自相关函数在不同循环频率上实现相关累积，因此输入信号的循环谱自相关函数在某些循环频率点处出现谱峰。

1.2 谱相关密度函数

平稳信号的自相关函数和功率谱密度函数是一对傅里叶变换对，同样，循环平稳信号的循环自相关函数和谱相关密度函数也是一对傅里叶变换对[4]。信号x（t）的循环自相关函数Rαx（τ）的傅里叶变换称为循环谱密度函数或谱相关密度函数，其中，XT（f）=即时域信号x（u）的傅里叶变换。

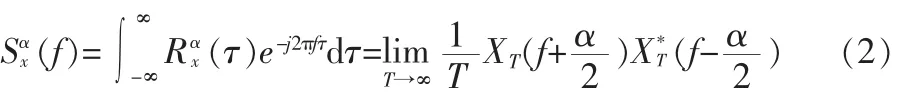
当α=0时，式（1）和式（2）退化为通常的自相关函数和功率谱密度函数，由此可见，循环谱自相关函数Rαx（τ）和循环谱密度函数Sαx（f）是传统自相关函数和功率谱密度函数Sx（f）的推广。由于大多数无人机采用BPSK调制信号，本文将以BPSK信号为例，实现循环谱对载频的估计。BPSK信号的循环谱表达式为：

φ0为初始相位，Tb为码元宽度，fc为载波频率。

BPSK信号的循环谱在α=±2fc+N/Tb、α=N/Tb、（N为整数）处出现谱峰，其中α=0及α=±2fc的谱峰值相等且最大。

1.3 谱相关密度函数的估计

通过时域或频域平滑的方法，可以得到对谱相关密度函数的估计。由于对信号的分析是在有限时间间隔Δt内进行，因此，谱相关密度函数是一个估计值。下面以时域平滑的方法对谱相关函数进行估计[5]。式（2）可重新写为

其中：

式中

Δt为信号分析的时间间隔，TW是短时傅里叶加窗长度，且为滑动短时傅里叶变换。如图1所示。在信号分析的有限时间间隔Δt内，频率分辨率Δt由短时傅里叶加窗长度TW决定，即Δf=1/TW。L表示在每次短时傅里叶变换中的重叠部分。为了避免频谱混叠和泄露，L的取值范围[6]应满足：L≤TW/4。

此外，该算法中还涉及到一个参数M=Δt/TW，即Grenander不确定条件[6]，M的取值应远远大于1。该不确定条件意味着信号分析的有限时间间隔Δt应远远大于短时傅里叶加窗长度。循环谱的循环频率分辨率由信号分析的时间间隔Δt所决定，即Δα=1/Δt。

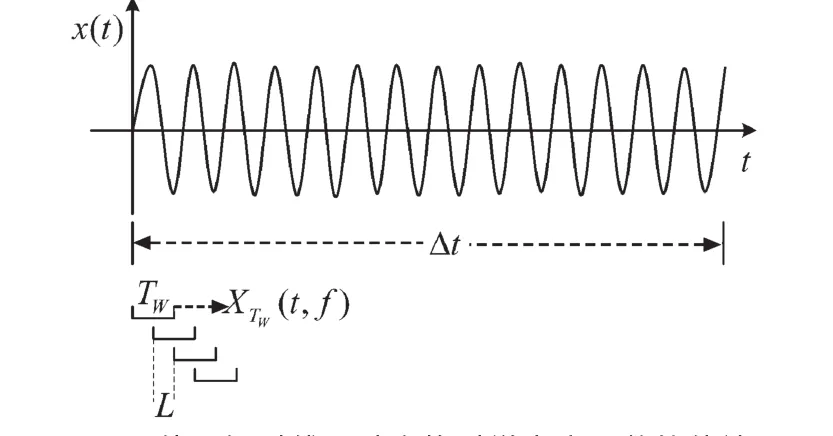
图1 使用短时傅里叶变换对谱密度函数的估计Fig.1 Using short-time Fourier transform to estimate the spectral density function

2 时域平滑FFT累加算法

由于循环谱的计算是在频谱频率——循环频率双频率平面上进行的，因此循环谱的计算量非常大。为了计算的有效性以及硬件实现的响应速度，有效的循环谱实现算法变的不可或缺。循环谱的计算有两种方法，一种是循环自相关函数的傅里叶变换的方法，一种是信号谱相关法，采用谱相关的数值计算法又可以分为时域平滑FFT累加算法和频域平滑FFT累加算法[5]。本节将详细介绍循环谱的时域平滑FFT累加算法。

我们将式（4）和式（5）改写为

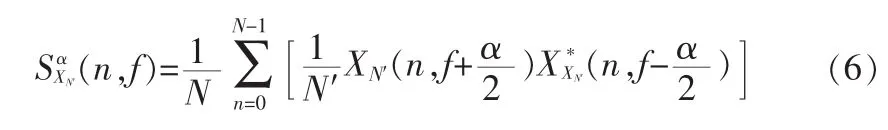
式中

XN′（n，k）为时域信号x（n）在经过数据加窗函数处理后的离散傅里叶变换，w（n）为数据加窗函数，N′为加窗后截取的信号长度，N为数据的总长度。该算法的实现步骤流程如图2所示。

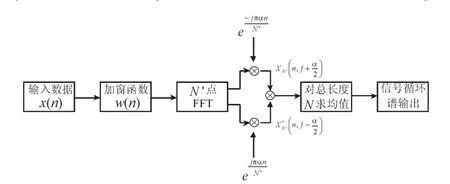
图2 时域平滑FFT累加算法步骤流程图Fig.2 The flow chart of time-smoothing FFT accumulation method

由图2可以看出，时域平滑FFT累加算法主要由三部分组成。首选，采用加窗函数对输入的时域信号进行加窗，并对每一个加窗后的截短序列，做N′点的快速傅里叶变换；然后将XN′（n，k）分为上支路和下支路两个支路分量，分别乘以循环系数e-jπαn/N′和ejπαn/N′，并将下支路信号取共轭，与上支路信号做乘积计算。最后，对所有的加窗截短序列求均值，即可得到信号在数据总长度的循环谱结果。

3 计算机仿真结果

根据前面循环谱的相关理论结果，并采用时域平滑FFT累加算法，对BPSK信号循环谱进行MATLAB仿真。试验数据的信号参数如下：信号码元个数为1 024；信息码元速率为20 Mbps；载波fc=2Rb，即4×107Hz；采样频率fs=4 fc；频率分辨率Δf=fs/64；Grenander不确定条件M=128，满足远远大于1的条件；循环频率分辨率为Δα=Δf/128；每次短时傅里叶变换中的重叠部分L=16。为了体现循环谱进行调制信号的参数估计可以摆脱平稳噪声的影响，我们设计了两组对比试验，试验一是理想无噪声污染信号，试验二为信噪比是-10 dB的加噪信号。噪声选用高斯白噪声。仿真结果分别为图3和图4所示。

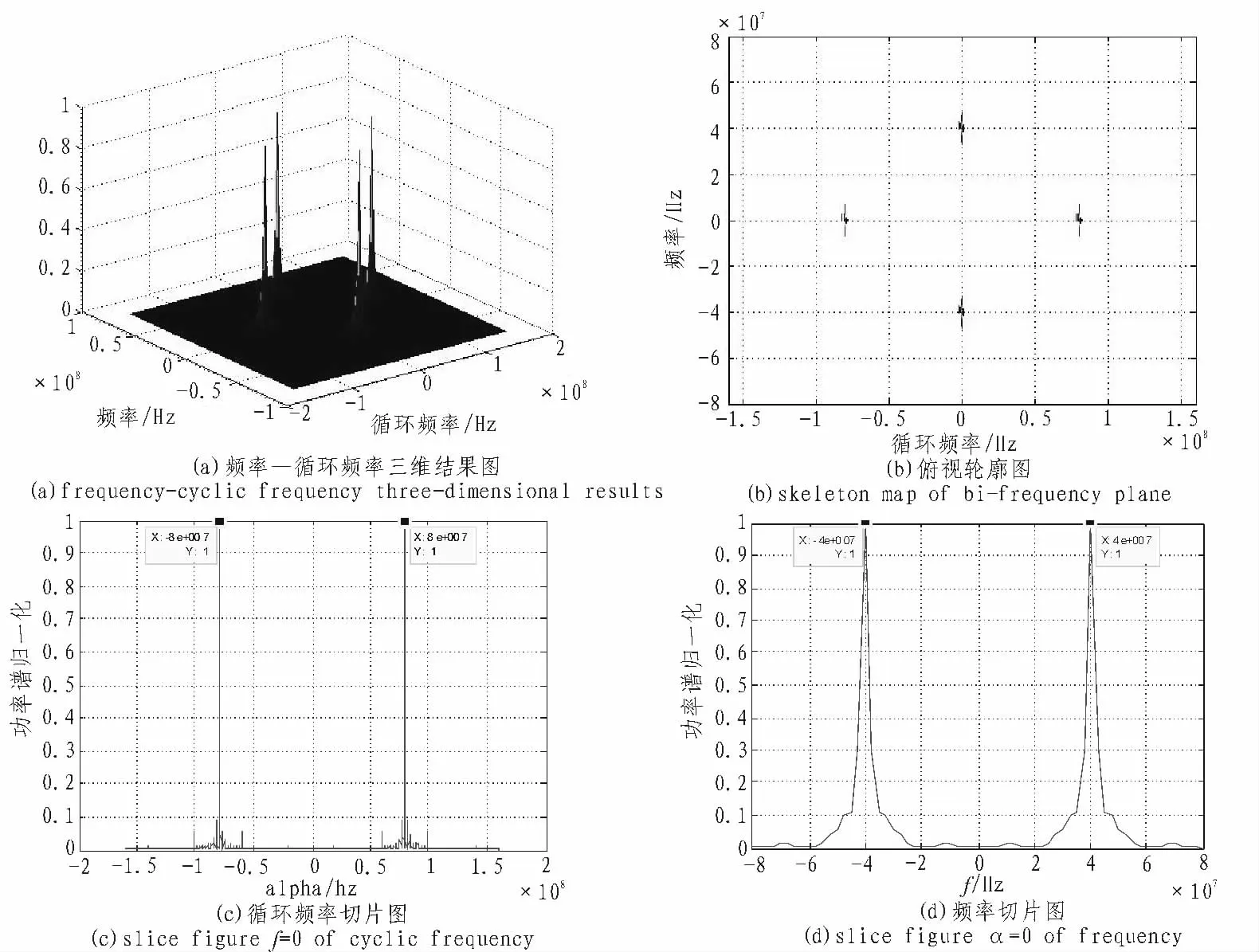
图3 无噪声时，BPSK信号循环谱仿真结果图Fig.3 The simulation results of BPSK cyclic spectrum when no noise

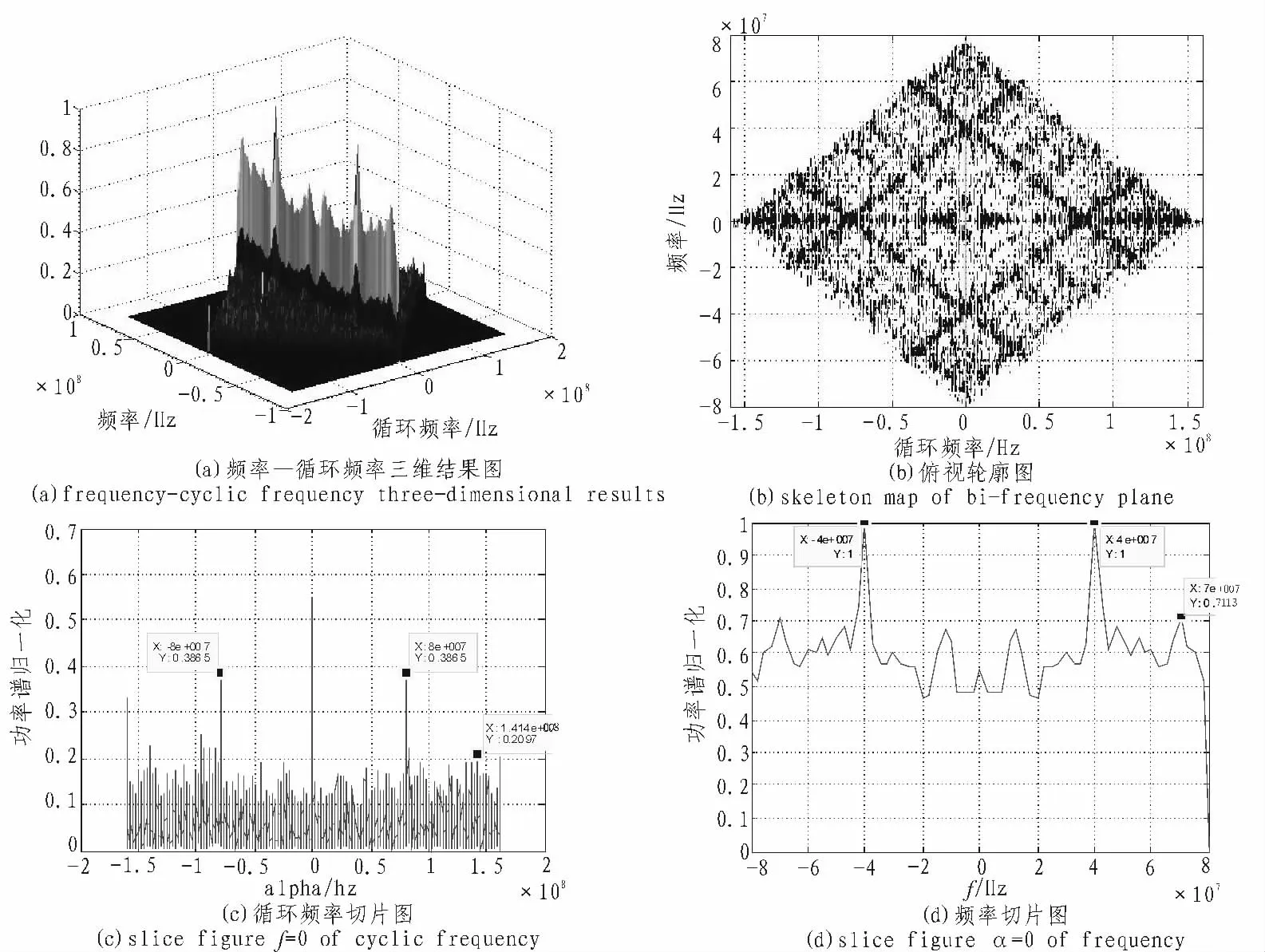
图4 信噪比-10 dB，BPSK信号循环谱仿真结果图Fig.4 The simulation results of BPSK cyclic spectrum when SNR is-10 dB

由前面的分析可知，BPSK信号的循环谱在α=±2fc+N/Tb、α=N/Tb（N为整数）处出现谱峰，其中α=0及α=±2fc的谱峰值相等且最大。且当循环频率α=0时，谱相关函数即为功率谱密度函数。

由图3（a）可以看出，在无噪声影响时，有4个非常明显的尖峰出现。对f=0做循环频率的切片图，可以准确的显示，在α=±2fc处，即8×107Hz，存在两个明显的峰值。对α=0做频率的切片图，和传统的功率谱分析一样，在载波fc处，存在2个明显的峰值。

当信噪比恶化到-10 dB时，如图4（c）所示的循环频率切片图上，在正半轴循环频率α=8×107和负半轴循环频率α=-8×107处依然有两个明显的尖峰存在，且对信号载波与干扰杂波进行信杂比（载波与最高干扰杂波谱线的功率比）分析，经计算可以得到其信杂比为10lg（0.3865/0.2097）=2.656 dB，而在频率切片图上，如图4（d）所示，用传统的功率谱分析可得信杂比为10lg（1/0.7113）=1.479 dB。可以看出在信噪比为-10 dB时，使用循环频率对信号载波的检测比功率谱检测，信杂比提高了1.177 dB。

从频谱带宽范围来看，采用循环谱估计方法得到的载波频率非常精确，是一根两倍的载波谱线。而传统功率谱估计方法会出现一定的带宽范围，这对由多普勒引起的载波频谱偏差，将出现一定的估计误差。

4 结论

本文从循环谱的基本理论开始论述，通过使用时域平滑FFT累加算法，实现了对BPSK信号的计算机仿真验证，证明了在低信噪比条件下，循环谱依然可以有效的检测信号的载波频率。因此，将循环谱检测技术应用到无人机数据链低信噪比信号的检测是一种非常有效的新方法。

[1] Roland E.Best.锁相环设计、仿真与应用[M].5版.李永明等译.北京：清华大学出版社，2007.

[2] Gardner W A.Measurement of spectral correlation[J].IEEE Trans.ASSP，1986，ASSP-34（10）:1111-1123.

[3] Gardner W A.The spectral correlation theory of cyclostationary time-series[J].Signal Processing，1986，11（1）:13-36.

[4] Gardner W A，Brown W A，Chen C K.Spectral correlation of modulated signal:part1-analog modulation[J].IEEE Transactions on Communication，1987，35（6）:584-594.

[5] Phillip E P.Detecting and classifying low probability of intercept radar second edition[M].Artech House，2009：513-530.

[6] Lima，A.F.，Jr.，Analysis of low probability of intercept radar signals using cyclostationary processing[D].Naval Postgraduate School Master’s thesis，2002.