基于流固耦合的泥浆泵剪切阀出口弯管应力与疲劳分析
裴勇毅, 罗静
(1.川庆钻探工程有限公司长庆钻井总公司机修公司,宁夏银川 750006;2.重庆大学机械工程学院,重庆400044)
1 引言
长庆钻井总公司所属钻井队现场使用泥浆泵时,剪切阀泄流出口管道设计为弯管回流型式(图1)。此结构工作原理为:当泥浆压力高于设定压力时,泥浆剪断安全销从上部直角弯管处流入下部低压五通管。这种设计的优点是简便易操作,现场不用搭建专用泄流管汇;缺点是当弯管处疲劳失效时会造成管材撕裂,高压泥浆喷出造成伤人事故。

图1 泥浆泵泄流结构
由于此种结构具有明显的优点,所以长庆钻井公司拟在所有钻井队推广使用,但是前提是此种机构的强度无安全隐患,因此需要研究直角弯管内流体的流场以及分析弯管的应力和疲劳强度,以确定结构的稳定性。
本文主要应用计算流体力学软件FLUENT分析了直角弯管内部三维流场情况,然后通过流固耦合[2],由有限元分析软件ANSYS对直角弯管结构进行应力分析以及疲劳强度分析。
2 直角弯管模型的建立
2.1 物理模型
钻井现场泥浆泵剪切阀出口直角弯管几何模型如图2所示,上端为泥浆的出口,下端为泥浆的回流口。泥浆出口速度为10m/s,出口压力为22MPa。
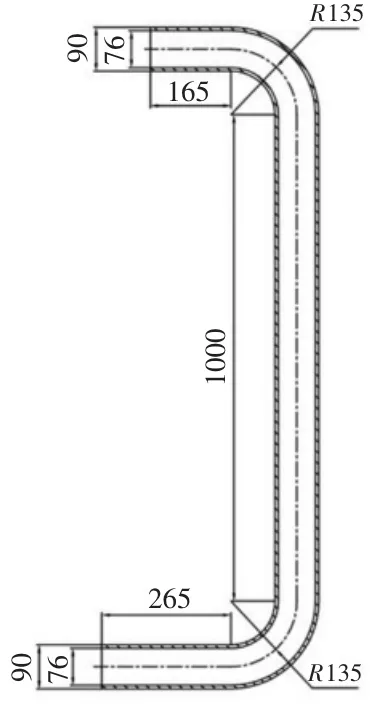
图2 直角弯管几何模型
2.2 网格模型

图3 流体域和固体域网格图
对流体域和弯管进行网格划分如图3所示,采用混合网格划分,并且对弯管的直角处进行了加密处理,内弧网格密度大于外弧网格密度。流体域共划分了241980个节点以及227940个单元,弯管共划分了146950个节点以及27448个单元。
3 计算方法
采用计算流体力学软件FLUENT软件对直角弯管内流体进行模拟分析,根据实际工况,湍流模型选用标准k-ε模型,边界条件为速度入口、压力出口。控制方程的传送选用压力-速度耦合的SIMPLE算法,差分格式使用二阶迎风,残差收敛标准选用10-3。
管道内流场分析通过FLUENT模拟后,求出压力载荷矩阵,并删除流体单元,保留固体管壁单元;流固耦合作用的力学模型及方程通过管壁的平衡协调关系引入[2],将压力载荷导入ANSYS对弯管进行应力和疲劳分析。由于实际情况下,此直角弯管的入口和出口均与另外的其他管道焊接,故对弯管的入口和出口的自由度进行全约束。
4 弯管流场分析
流体通过弯管上端后,在压力、重力和管壁摩擦力的作用下沿着弯管运动。对弯管内的流体进行动力学分析,图4为弯管速度云图。可以看出随着流体流经弯管,流动速度在弯管入口内侧由小变大,而在外侧则由大变小;弯管中部外侧和弯管出口外侧流速较大;弯管内流体流动很不均匀,湍流现象非常显著。
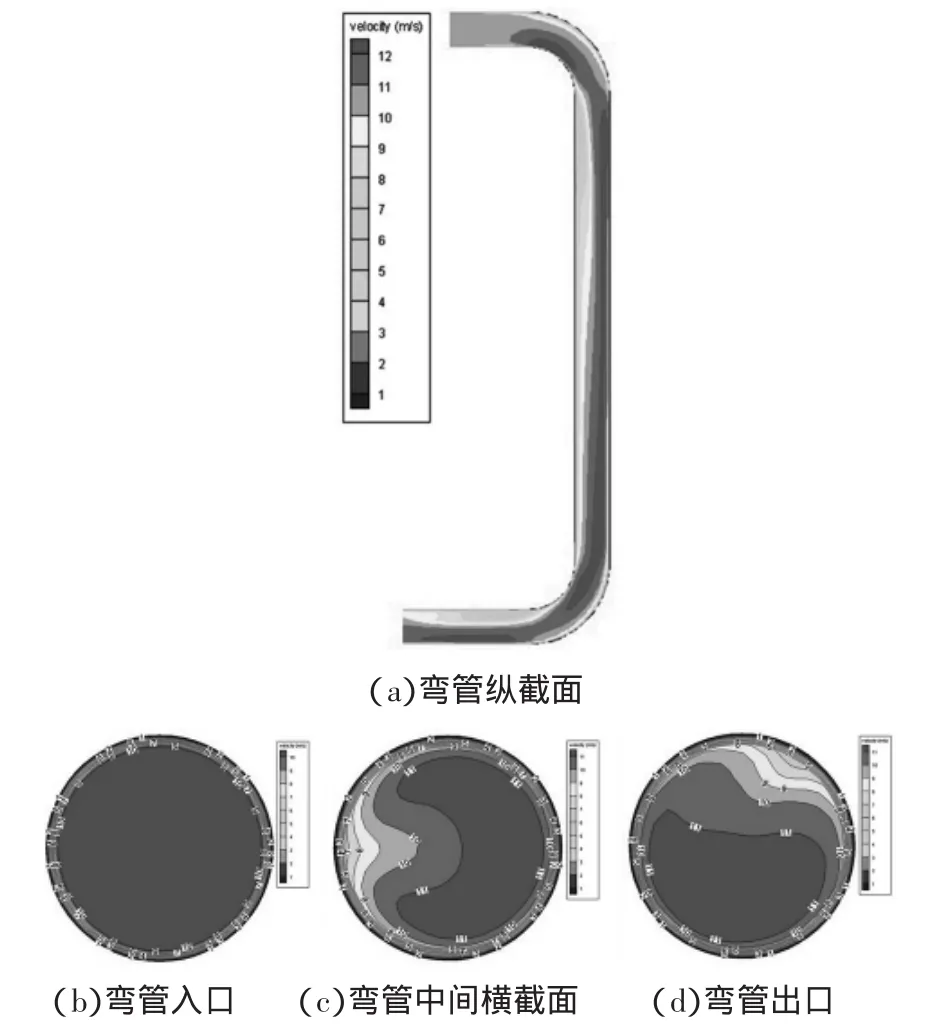
图4 弯管速度云图
图5为弯管纵截面压力云图,可以看出弯管内流体压力分布也极不均匀。在直角弯道处,由于流体在流动的过程中受到弯管曲率的影响,流体在离心力的作用下被甩到曲率半径较大的外侧壁面处,出现压力集中,导致弯道外侧压力增大,内侧压力减小;内侧的流体在惯性力的作用下流速加大,出现分离现象。而且由于能量的损失,导致此弯管下游段的压力均值小于上游段的压力均值。
图4、图5的速度和压力云图很好地解释了二次流现象[4-5],管道内的流体流速由单一流向变为双向流动(沿管道轴向的主流动和沿管道截面径向闭合的二次流动)。在直角弯道处,流体流动由于受到管道曲率的影响,产生了平行于内侧的偏移,靠近内侧的流体层由于速度较小,比外侧(离边界较远的流体层)偏移得厉害,导致了叠加于主流之上的二次流。

图5 弯管纵截面压力云图
5 直角弯管应力分析
根据流固耦合原理采用有限元分析软件ANSYS对直角弯管进行应力分析。通过软件FLUENT计算的流体压力作为载荷加载到直角弯管内部面上,如图6所示。由于直角弯管上下端均与其他管线固接,故直角弯管上下端面均采用固定约束。
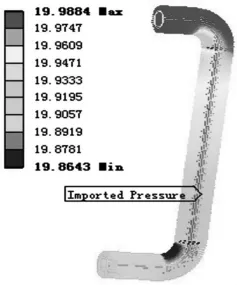
图6 流固耦合作用图(MPa)
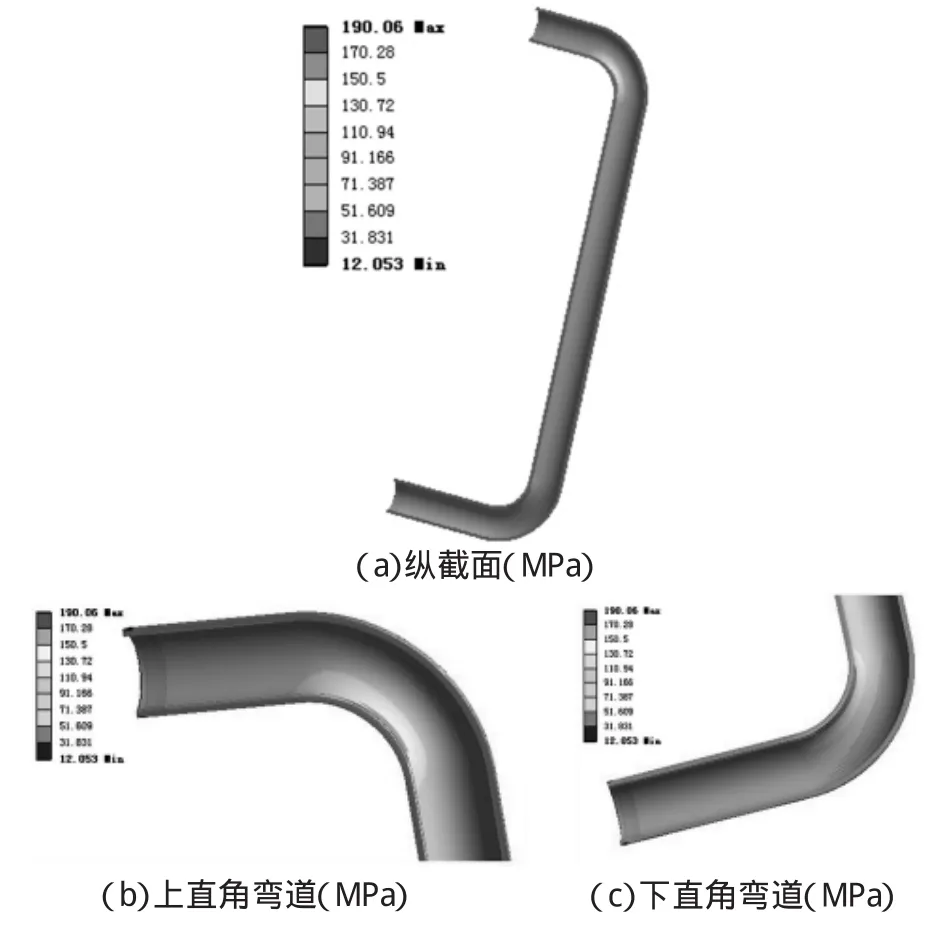
图7 直角弯道弯管Equivalent Stress(von-Mise)应力云图
流固耦合模拟分析后,图7为直角弯管Equivalent Stress(von-Mise)应力云图。从该图可以看出最大的Equivalent Stress(von-Mise)应力出现在该弯管下端出口附近,这是因为边界条件中对弯管的入口和出口进行自由度全约束。直角弯管为20钢无缝钢管,屈服强度为245MPa,该分析中最大应力在直角弯管的出口附近,为190.06MPa,小于材料的屈服强度,所以直角弯管结构从静力学的角度来看,其强度是足够的。而且在弯管直角管壁内侧也有明显的应力集中,为150.5MPa~170.28MPa这与文献[6]分析结果(无椭圆度等壁厚的弯管最大应力靠近弯管内侧)相同。
6 直角弯管疲劳分析
直角弯管在高频率的载荷下,即使最大应力没达到弯管材料的许用应力,其结构一样可以破坏,即产生疲劳破坏;同时应力越大,失效的循环次数就越小。而且由于直角弯管结构所受流体对它的压力是一个动载荷,仅从静力学的角度考虑其强度是不够的,所以还需对直角弯管进行动载荷下的疲劳寿命分析。
弯管为20钢无缝钢管,其S-N曲线如图8所示。载荷类型选用脉动循环载荷,载荷按正余弦曲线规律变化,且载荷比例由0到1波动。考虑到平均应力对疲劳寿命的影响,在应力修正模型中,Soderberg直线模型过于保守,Gerber抛物线模型会过于危险,Goodman直线模型和折线模型比较适合,故选择Goodman直线模型估算疲劳寿命。
模拟分析得出相应的疲劳寿命云图如图9所示。从图中可以看出,直角弯管回流口处为疲劳寿命最薄弱的地方,疲劳寿命循环次数为1.672×105次。而且弯管上下两直角弯道内侧疲劳寿命也比较薄弱,疲劳寿命循环次数为4.5161×105~6.7202×105次,可以看出其疲劳寿命的规律和Equivalent Stress(von-Mise)应力规律一致。
图10为直角弯管的Fatigue Senstivity(疲劳敏感性)图,可以看出在临界区域,载荷比例为0.75之前,弯管的疲劳寿命稳定在106次,在载荷比例超过0.75后,疲劳寿命随着载荷比例的增加而减少。
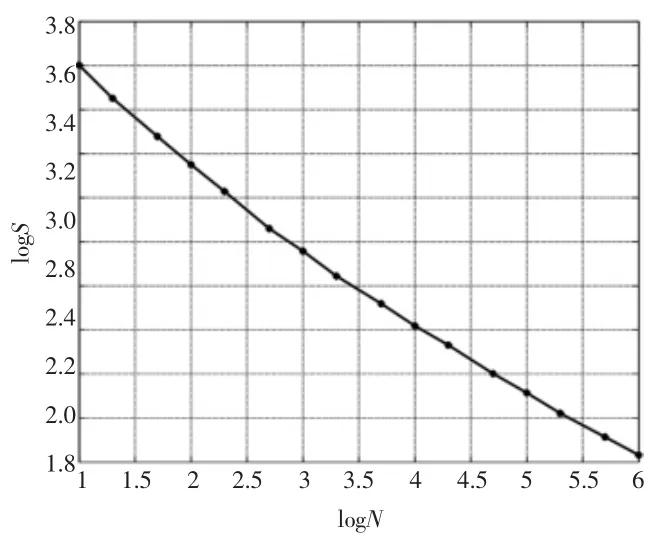
图8 20无缝钢管S-N曲线
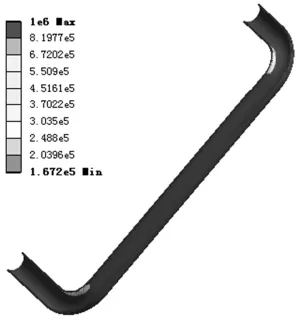
图9 直角弯管Life(疲劳寿命)云图
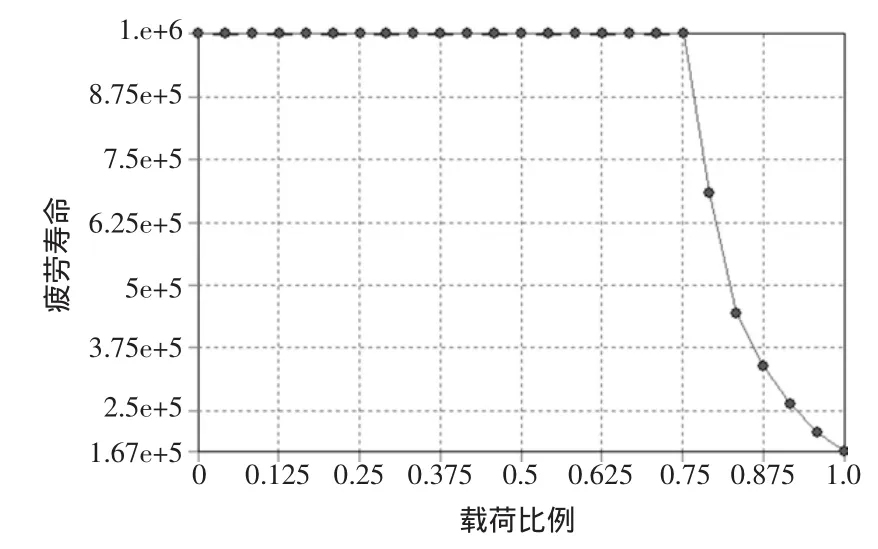
图10 直角弯管Fatigue Senstivity(疲劳敏感性)图
7 结论
利用计算流体力学软件FLUENT对直角弯管流体域进行流场分析,得出管内流体流速分布规律与实际情况基本吻合。即随着泥浆流经弯管,流动速度在弯管入口内侧由小变大,而在外侧则由大变小;弯管中部外侧和弯管出口外侧流速较大;弯管内流体流动很不均匀,湍流现象非常显著,并伴有明显的二次流现象。
然后根据流固耦合原理采用有限元分析软件ANSYS对直角弯管进行分析,得出其最大Equivalent Stress(von-Mise)应力出现在弯管下端出口附近,在弯管直角管壁内侧也有明显的应力集中。
最后根据所求的弯管材料的S-N曲线方程以及有限元分析软件对弯管寿命进行分析后,可得出疲劳寿命的规律和Equivalent Stress(von-Mise)应力规律一致,即出口处以及上下两直角弯道内侧疲劳寿命比较薄弱。Fatigue Senstivity(疲劳敏感性)表明在临界区域,载荷比例为0.75之前,弯管的疲劳寿命稳定在106次,在载荷比例超过0.75后,疲劳寿命随着载荷比例的增加而减少。
综合以上分析可以看出,此种结构是完全可以满足安全要求的,可以实现现场的推广应用。
[1] 中国压力容器学会管道委员会,等.第三届全国管道技术学术会议压力管道技术研究进展精选集[C].北京:机械工业出版社,2006.
[2] 偶国富,许根福,朱祖超,等.弯管冲蚀失效流固耦合机理及数值模拟[J].机械工程学报,2009,45(4):119-124.
[3] TAYLOR A M K P,et al.Curved ducts with strong secondary motion:velocity measurements ofdeveloping laminarand turbulent flow[J].Transactions of the ASME,1985,104:350-359.
[4] 朱立明,柯葵.流体力学[M].上海:同济大学出版社,2009.
[5] 杜明俊,等.多相混输管道90°弯管冲蚀破坏应力分析[J].油气储运,2011,30(6):427-430.
[6] 马爱梅,鹿晓阳,陈红艳.基于流体动力学的弯管应力有限元分析[J].机械设计,2006,23(3):50-52.

