正弦振动的数学描述与试验技术

肖荣军，陈贵如

（1.中国科学院半导体研究所元器件检测中心，北京 100083 2.北京市新能源汽车发展促进中心，北京 100101）

引言

正弦振动是运动量随时间按正弦(或余弦)函数变化的振动，常在电工电子产品和舰船、飞行器、各类车辆等存在旋转、脉动、振荡现象的装置上出现。

正弦振动试验就是在试验室模拟电工电子产品和舰船、飞行器、各类车辆等系统在运输、贮存、使用中所经受的振动，并考核其适应环境的能力。

正弦振动试验有定频和扫频两种试验类型，扫频试验又有线性和对数两种扫描频率方式。

1 正弦振动的数学描述

振动是物体围绕平衡位置进行往复运动，通常以振动体的一些参数(如位移、速度、加速度)随时间变化的函数来表征振动的时间历程。我们可以将振动看作是一个质点或物体对于一个基准位置的运动。振动的时间历程分为非周期振动和周期振动。非周期振动在图形上不重复，不能用简单的函数关系来描述。周期振动是经过一定的时间间隔后仍精确地重复的运动，可以用振动位移x(t)为时间t的函数关系表示

周期振动的最简单形式是简谐振动，其时间历程是正弦或余弦曲线，环境试验中一般用正弦曲线来描述。

1.1 正弦振动可用下述函数描述

式中ω=2πf 为角频率(f-振动频率)

X —位移，D —最大位移(即单振幅位移，简称振幅,单位mm)，t —时间，φ —初相角。

为方便计算，对振动试验可取φ=0，则

运动质点的速度是位移对时间的变化率，即速度是位移函数(4)的导数

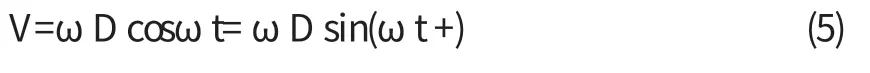
当sin(ωt +)=1时，V取峰值

Vp=ωD(mm/s)=2πfD×10-3(m/s)

加速度是速度对时间的变化率，所以加速度是速度函数的导数

当sin(ωt +π)=1时，A有峰值

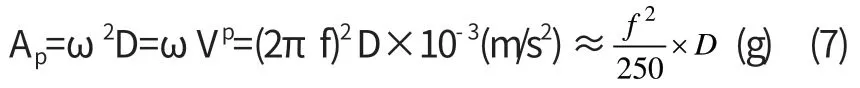
其矢量表示法如图1所示：矢量D以等角速度作逆时针旋转，其在纵轴上的投影表示质点的运动。振动位移、速度、加速度的振动频率均为f=，周期为T=。速度矢量超前位移，加速度矢量超前速度矢量。

1.2 振动幅值描述量及其相互关系

根据需要，振动幅值具有不同的描述量，其相互关系如图2及表1。

2 正弦振动试验技术

做正弦振动试验除了要掌握设备的操作技术外，还应当掌握有关振动的理论知识，必要时还要进行参数计算。

2.1 首先根据下式计算振动台的推力能否达到试验要求

式中：F—推力(激振力)(N)

m1—振动台运动部分有效质量(kg)

m2—辅助台面质量(kg)

m3—试件质量(kg)

m4—夹具、安装螺钉质量(kg)

A— 试验加速度(m/s2)

例 如：当m1=5kg，m2=10kg，m3=35 kg，m4=50kg，A=49 m/s2时，F=4900N。

根据经验F应略偏高，需乘系数1.2，则 F应=1.2F=1.2×4900N=5880N。所以当设备推力大于等于5880N时，可以试验。

2.2 验证速度和位移是否满足要求

用公式V=A/2πf或者公式 V=2πfD ×10-3验证速度是否小于等于振动台的额定速度。例如：

V = A/2πf = 196/2×3.14×80.8≈0.39 m/s

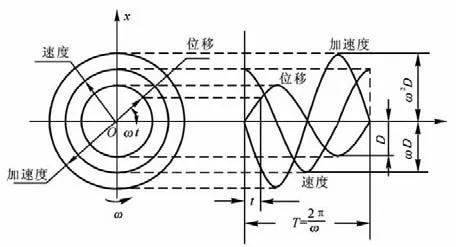
图1 简谐振动的矢量表示法[2]

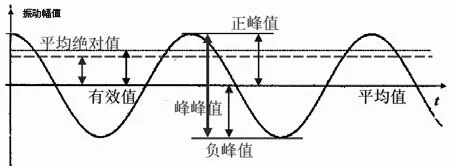
图2 振动幅值描述量

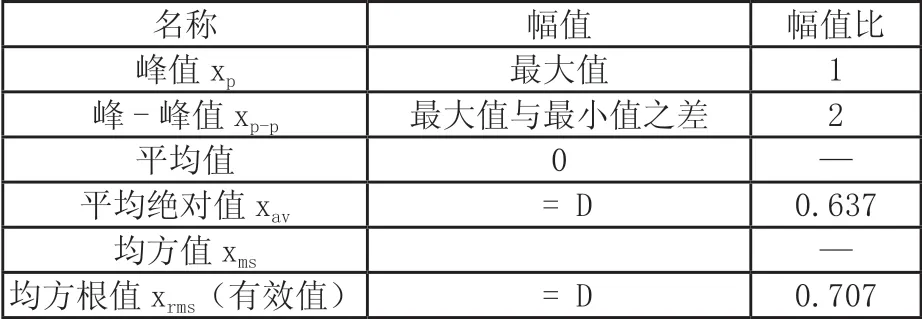
表1 振动幅值描述量的相互关系

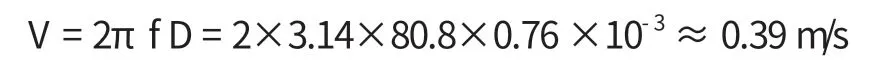
如果速度小于等于振动台的额定速度，则可以试验。

2.3 定振级扫频试验平滑交越点频率

交越频率是振动试验中一种振动特性量变为另一种振动特性量时的频率，该频率点称为交越点。在交越点两种振动特性量值都能得到满足，故称为平滑交越点，该点的频率称为平滑交越频率。

正弦振动试验可以规定一个交越点，也可以规定多个交越点。对只有一个交越点的试验，通常在交越点以下位移恒定，加速度成正比例变化，因为低频时对产品影响的主要是位移量；在交越点以上加速度恒定，位移成反比例变化，因此在高频段位移量变得很小，加速度幅值相对较大，根据加速度正比于作用力的原理，此时，对产品影响的主要是加速度量。对有多个交越点的试验，可以定位移—定加速度—定位移—定加速度等，也可以定位移—定速度—定加速度等。

平滑交越频率是重要的试验参数，在试验时非常重要，有时需要计算才能得到。

2.3.1 加速度与速度平滑交越点频率(Hz)的计算公式

2.3.2 速度与位移平滑交越点频率的计算公式

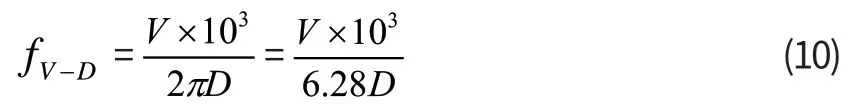
2.3.3 加速度与位移平滑交越点频率的计算公式

公式(11)亦可简化为：

公式(11)是上述3个公式中最重要的，实践中经常用到，例如：GJB 548B-2005 规定器件作等幅简谐振动“振幅两倍幅值为1.52mm±0.15mm”，“峰值加速度按试验条件A、B或C的规定(20%,0)m/s2,在交越频率以下，试验条件应由振幅大小控制，在交越频率以上试验条件应由峰值加速度控制。”[3]

该标准给出了两倍振幅、峰值加速度，但未给出交越频率，需要计算，以条件A为例：

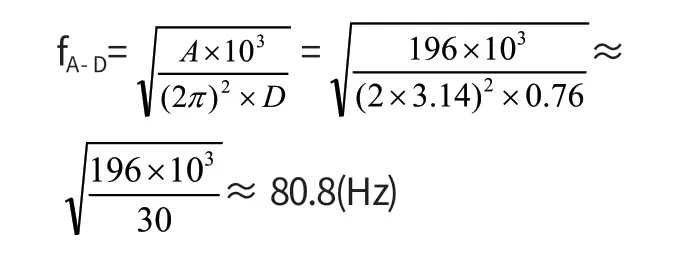
同理可求另外两个条件的交越频率。结果如表2。

加速度幅值20g的试验曲线图如图3。图中横坐标频率由10Hz到2000Hz，纵坐标为加速度（g），拐点即交越点（0.76mm，20g ，80.8Hz）。

2.4 扫描时间和扫描速率的确定

2.4.1 线性扫描：

式中：S1—扫描时间(s或min)

fH-fL—扫描宽带，其中fH为上限频率，fL为下限频率(Hz)

V0—扫描速率(Hz/min或Hz/s)

2.4.2 对数扫频

2.4.2 .1 倍频程

频率比为2n的两个频率之间的频段称为n个倍频程，即fH/ fL=2n[4]，该式两边取以2为底的对数：log2fH/fL= log22n=n，则

式中： n—倍频程(oct)

fH—上限频率(Hz)

fL—下限频率(Hz)

例如：GJB 360-2009 中4.4 规定在10Hz～55Hz～10Hz范围内连续来回定位移扫频，“对数扫频：扫频速率为1oct/min。[5]”就需要计算倍频程从而决定扫频时间。

所以，来回扫频一次需要2×2.5= 5min。

值得关切的是，正弦对数扫描指相同时间扫过的频率倍频程数是相同的，n就是下限频率到上限频率经过了n个倍频程。例如从10～40Hz是两个倍频程，从100～400Hz也是2个倍频程，在对数扫描的情况下，扫过这两段的时间是相同的，就是说对数扫描低频扫得慢而高频扫得快。其结果是虽然在高频段振动频率较高，但在每个频率点上的扫描停留时间较短[6]，而在低频段情况则正好相反。

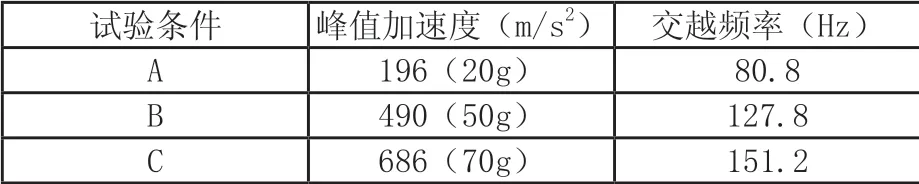
表2 三种试验条件下的峰值加速度和交越频率

图3 GJB 548B-2005 试验条件A 试验曲线图

2.4.2 .2 扫描速率与扫描时间的换算

式中：R—扫描速率(oct/min或)

fH—上限频率(Hz)

fL—下限频率(Hz)

T—扫描时间

n—倍频程(oct)

由(15)式可得

3 结语

正弦振动特别是正弦扫频振动是环境试验常用的试验方法，在国标、国军标和有关行业标准都有规定，但是这些标准并没有将试验所需的参数值全部给出，如上文中的GJB 548B-2005就没有给出交越频率和单峰位移，需要试验人员进行计算才能得到。实践中，常出现试验人员不知道计算交越频率的情况，没有遵循在低频段定位移，高频段定加速度的试验规则，从而不能进行正常试验，或者使样品经受过于严酷的试验条件，造成不必要的损失。本文通过对正弦振动的系统阐述，从数学描述中推导出参数的计算公式，并且列举了计算与试验实例，可以为检测人员提供指导，正确完成试验。

[1]邱景湖，钟琼华. 振动台与振动试验介绍[EB/OL].: http://www.KeKaoXing.com，2004-12.

[2]刑天虎. 力学环境试验技术[M]，西安：西北工业大学出版社，2003：29

[3]GJB 548B-2005. 微电子器件试验方法和程序[S].

[4]胡志强，法庆衍，洪宝林. 随机振动试验应用技术[M]. 北京：中国计量出版社，2003：174

[5]GJB 360B-2009. 电子及电气元件试验方法[S].

[6]陈福利. 正弦扫频振动试验方法的初步探讨[J]. 光电对抗与无源干扰，2001,（4）：51