基于残差重构的分布式视频压缩感知❋
常侃,覃团发,唐振华
(广西大学计算机与电子信息学院,南宁530004)
基于残差重构的分布式视频压缩感知❋
常侃❋❋,覃团发,唐振华
(广西大学计算机与电子信息学院,南宁530004)
为了改进分布式视频压缩感知方案的性能,提出了一种基于残差重构的分布式视频压缩感知方案。该方案在编码端逐帧独立进行测量,在解码端依靠视频信号的时域相关性提升重构信号质量。首先,对关键帧独立进行重构;其次,利用已重构关键帧做运动估计/运动补偿以生成非关键帧的边信息;接下来,对边信息采用与编码端相同的测量矩阵进行测量并计算测量残差值;最后,采用全变分最小化重构残差信号值并将其与边信息相加生成最终的重构图像。实验结果表明,在相同采样率下,与已有的分布式视频压缩感知方案相比,提出的方案可获得2.8 dB以上的峰值信噪比增益。
压缩感知;分布式视频压缩感知;残差重构;全变分最小化;边信息
1 引 言
分布式视频编码(Distributed Video Coding,DVC)[1]是一种特殊的视频编码框架。这类框架在编码端对各帧进行独立编码,在解码端则对连续的视频帧进行联合解码以获取更高质量的解码结果。与传统混合视频编码框架不同,DVC把计算量较大的运动估计(Motion Estimation,ME)/运动补偿(Mo-tion Compensation,MC)操作转移到解码端,具有“轻编码、重解码”的特点,特别适合于电力和计算能力有限的应用场合,例如无线多媒体传感器、无线视频监控、基于移动设备的视频会议等。
压缩感知(Compressed Sening,CS)[2]是近年在信号处理领域得到广泛重视的新兴理论体系。该理论指出,若某个待采样信号是稀疏的(或者在某个变换域是稀疏的),那么我们从其有限的(远低于原始信号维数)不相关测量值中准确恢复出原始信号的可能性极高。该理论突破了奈奎斯特采样定理的限制,使得信号获取的复杂度大大降低。CS的测量过程运算量较低,而重构过程则需要迭代求解最优化问题,复杂度相对较高。因此,CS理论结构特别适合各类分布式应用。
为了结合CS与DVC的优点,已经有一些学者将CS理论应用于DVC框架,设计分布式视频压缩感知(Distributed Compressed Video Sensing,DCVS)框架。其中,Kang等人在解码端采用GPSR(Gradient Projection for Sparse Reconstruction)方法对关键帧进行独立重构,采用非关键帧与边信息(Side Information,SI)间的相关性改进非关键帧的GPSR重构过程[3]。但是,Kang的方法没能很好地利用时域相关性,因此信号的重构质量不高。Do等人采用已重构关键帧中的空域相邻块对待重构非关键帧中的块进行稀疏表示,以提高SI的准确性[4]。在Do的方法中,SI的生成需要块信号的测量值,而一般来说,帧级别测量比块级别测量的性能更好;另外,SI的生成需要逐块求解l1最小化问题,复杂度很高。文献[4-5]都在重构端对非关键帧进行预测,并对预测值进行测量,最后对测量残差值进行重构。在预测准确的前提下,残差信号比原始信号在变换域下更为稀疏,因此残差信号的重构误差在很大概率上要小于原始信号的重构误差。但是,文献[5]首先对非关键帧进行独立重构,其次以已重构关键帧为参考进行ME/MC,然后再次对非关键帧做残差重构。为了保证重构质量,上述过程还需迭代n次(一般取5次),可见解码复杂度很高,并不实用。
为了提高DCVS方案的重构信号质量,本文提出了一种基于残差重构的DCVS方案。该方案利用相邻关键帧迭代进行1/4精度的ME/MC操作以保证SI的准确性;对SI进行测量,并对测量残差值进行全变分最小化(Total Variation Minimization,TVmin)重构。与Kang的方案相比[3],本文方案没有过多增加解码端负担,却较大幅度地提升了非关键帧的重构质量。
2 压缩感知理论
CS理论[2]的出现,突破了香农采样定理的瓶颈,降低了对传感器件分辨率的要求,使得超高分辨率信号获取成为可能。具体地,假设x是n维原始数据,Φ是m×n维测量矩阵(m≪n),y是m维测量数据。投影的过程可以采用公式描述如下:

若原始信号x足够稀疏,则可以将信号重构过程转换为一个最小l0范数的最优化问题:
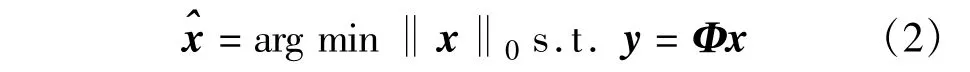
若x本身不稀疏,但是在某种基Ψ下稀疏,则可以通过求解以下l0范数的最小化问题来重构基Ψ下的原始信号:
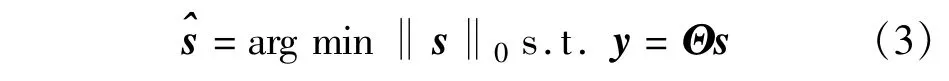
其中,Θ=ΦΨ,x=Ψs。
在CS理论中,传感器并不是直接获取信号x本身,而是获取其在测量基Φ上的投影值。对于测量矩阵Φ而言,希望其与稀疏矩阵Ψ不相干,这样所需的测量数为
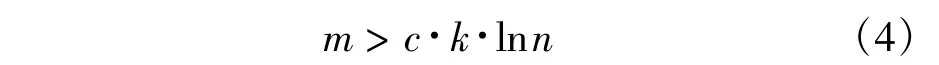
其中,k是x在Ψ下的非零值个数,c是常数。
比较普遍的方法是选取Φ为随机矩阵,因为随机矩阵与任何稀疏基都能以极大的概率不相干。但是,采用此类矩阵需要较高的内存开销和计算量,所以并不实用。Gan等人提出了结构化的随机矩阵(Structurally random matrix,SRM)[6],在该方法中,首先对输入信号进行随机置乱,其次进行简单、高效的变换(例如DCT或哈达玛变换),最后做随机下采样操作。测量值的产生仅需要少量的计算和内存开销,并不需要存储庞大的测量矩阵。鉴于该方法的良好性能,在本方案中编码端采用SRM方法进行测量。
由于求解l0范数的最小化问题是NP难,目前已有很多替代解法,其中最著名的方法是基追踪(Basic Pursuit,BP)算法,该方法将最小化l0范数问题转化为求解最小化l1范数问题,即

求解BP问题的复杂度较高,当信号的维度较高时(例如图像与视频信号),信号重构过程所需时间过长,使得CS的实用性降低。为提高信号的重构速度,出现了基于梯度下降的方法(如GPSR[7]),并出现了许多贪婪算法,如正交匹配追踪(Orthogonal Matching Pursuit,OMP)[8]等。
对于图像/视频信号而言,可以采用TVmin来取代l1最小化,从而更好地反映图像/视频信号的特征。TVmin由Candes等人引入CS中作为图像/视频信号的重构方法[2]。经典的求解TV最小化的方法是采用内点法迭代求解log-barrier问题,但是需要较高的复杂度,并不实用。Li将TV最小化问题转化为Augmented Lagrangian问题的形式,并将该问题拆成两个子问题交替求解,大大简化了求解过程[9],该方法被命名为TVAL3。本文采用TVAL3算法进行信号重构。
3 基于残差重构的DCVS方案
3.1 整体结构
在编码端,将视频序列划分为若干图像组(Group of Pictures,GOP),每个GOP包含一个关键帧和若干非关键帧,对关键帧和非关键帧均独立采用SRM[6]进行CS测量,关键帧的采样率需大于非关键帧的采样率。
解码端的重构总体流程如图1所示。首先重构每个GOP中的关键帧——对关键帧的测量值独立采用TVAL3算法[9]求解TVmin问题;其次,采用相邻已重构关键帧经过1/4精度的迭代ME/MC操作生成非关键帧SI值;接下来,利用非关键帧的测量值及SI逐帧进行残差重构。

图1 解码端图像重构总流程
非关键帧的残差重构过程如图2所示,具体包括如下步骤:
步骤2:计算测量残差值yr=y-;
步骤3:对yr采用TVAL3算法[9]求解TVmin问题,得到重构结果;

图2 非关键帧残差重构流程
3.2 残差重构
残差重构是本文提出的DCVS结构的核心,下面详细对该方法的流程和性能进行分析。
假设原始信号为x,采用测量矩阵Φ进行测量,得到测量值y。在本文算法中,并不直接采用测量值y进行重构,而是采用残差重构的方法。具体地,假设在重构端有待重构信号的预测值,对预测值进行测量,得到
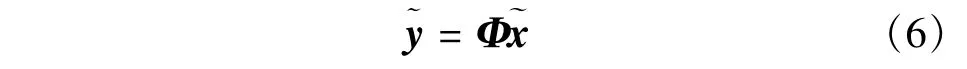
其次,求实际测量值与预测测量残差值:

从公式(7)可知,yr实际上就是原始帧与预测值的残差xr做随机投影的结果。假设为从yr中恢复出来的残差信号,则可以通过下式获取原信号x的重构值:

根据上述流程,原始信号x的重构误差为
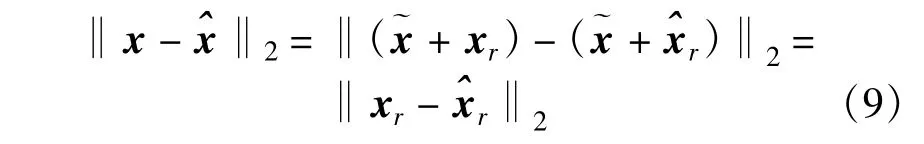
根据式(9)可知,在残差重构算法中,原始信号x的重构误差由预测残差xr直接决定。另一方面,若与x足够接近,则xr定会比原信号x更为稀疏。因此,采用CS重构算法从yr中恢复xr会比从y中恢复x的误差更小。由此可以推断出,残差重构算法可以比直接重构算法获得更好的重构质量。
3.3 边信息生成
为了保证SI准确性,在Do的方法中[4],需要逐块求解l1最小化问题以获取当前预测块的稀疏表示;而在Mun的方法中[5],则需要先直接重构非关键帧,接着多次迭代进行“ME/MC-残差重构”操作。两种SI生成方法的复杂度都过高,并不实用。
类似于DVC[1],可以通过在关键帧之间进行ME,并对运动矢量调整后进行MC得到SI。在本文方案中,首先对关键帧进行6-tap FIR滤波器插值得到1/2像素精度图像,继而进行双线性插值得到1/4像素精度图像;之后在前后两个关键帧之间双向迭代进行1/4像素精度的ME/MC操作。图3给出了GOP大小为4时的双向迭代ME/MC结构。

图3 双向迭代ME/MC结构
4 实验结果及讨论
为了测试算法性能,在MATLAB平台上仿真了本文方案,并与Kang的方法[3]进行比较。GOP大小设定为4,关键帧的采样率固定为0.7,对于非关键帧,分别采用0.1、0.2、0.3、0.4和0.5 5种采样率。用于信号测量的SRM选用哈达玛变换;用于信号重构的TVAL3算法中的μ选为212,β选为26,外循环门限设为10-6,内循环门限设为10-3,最大迭代次数设为150。采用的测试序列为CIF格式的“foreman”与“football”,帧率为30 frame/s。“foreman”序列含有较慢的运动,相对较平缓;相比之下,“football”序列细节信息丰富,包含快速运动。
表1列出了两种方法在5个采样率下的非关键帧重构图像的平均峰值信噪比(Peak Signal to Noise Ratio,PSNR),图4和图5则更直观地显示出了非关键帧重构图像PSNR值随采样率变化情况。
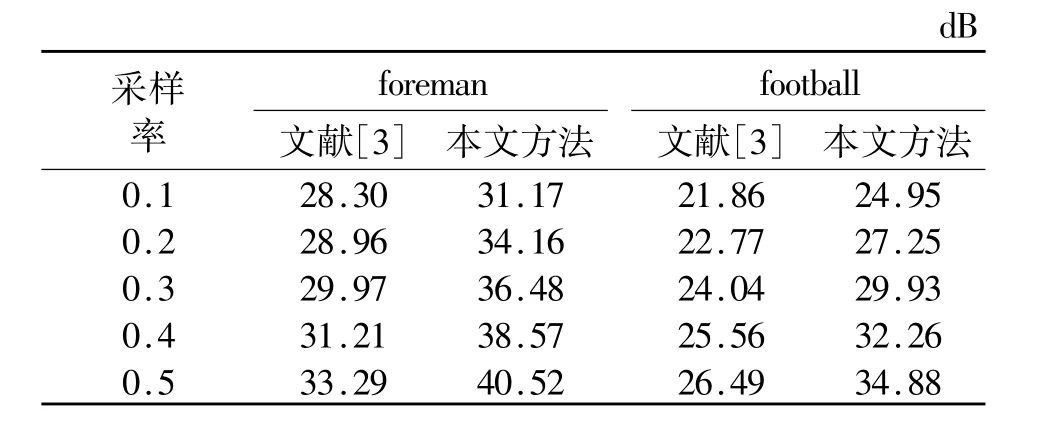
表1 非关键帧重构质量比较Table 1 Reconstruction quality comparison for non-key frames

图4 “foreman”序列PSNR比较
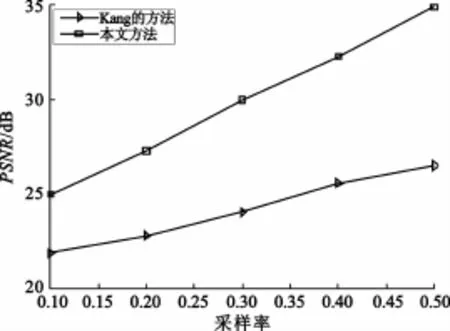
图5 “football”序列PSNR比较
从表1和图4、图5中可以总结出,首先,在相同的采样率下,本文方法比Kang的方法有较高的PSNR提升;随着采样率的升高,本文方法PSNR提升值逐渐增大。例如,对于“foreman”序列,在0.1的采样率下,本文方法可以获得2.87 dB的PSNR增益;当采样率提升到0.5时,该值提升到7.23 dB。其次,当序列中含有快速运动和丰富细节信息时,本文方法的非关键帧重构图像质量下降,主要原因有二:第一,丰富细节信息导致关键帧重构质量下降;第二,快速运动导致生成的SI准确性降低。
图6和图7分别展示了“foreman”序列与“football”序列的SI与残差值(取绝对值显示)。由于“foreman”序列运动缓慢,因此SI较为准确,图6中的残差值很小。在此情况下,采用TVAL3算法求解TVmin问题,整帧图像的离散梯度值较稀疏,因此可断定重构效果较好,该分析结论也与表1的实验结果吻合。相比之下,“football”序列包含快速运动,生成的SI失真较大,图7(b)中的残差图像梯度值不够稀疏,因此求解TVmin问题的效果明显差于“foreman”序列。

图6 “foreman”序列第6帧SI与残差值
5 结束语
本文将残差重构方式引入DCVS方案,并且综合应用了双向迭代的SI生成方法,充分利用了视频信号的时域相关性。依据实验结果可知,在SI准确的前提下,残差重构方案可以较大幅度地提升重构信号质量,从而证明了残差重构方案的有效性。需要注意的是,本文方案未考虑测量值的量化和熵编码问题。虽然量化和熵编码可以有效降低输出数据量,但是量化对非线性重构结果的影响还需要进一步地研究和分析。因此,下一步的工作重点是将量化和熵编码合理、有效地引入到提出的DCVS方案中,以进一步推进DCVS方案的实用化。
[1]Guillemot C,Pereira F,Torres L,et al.Distributed monoview andmultiview video coding:basics,problems and recent advances[J].IEEE Signal Processing Magazine,2007,24(5):67-76.
[2]Candes E,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[3]KANG Li-wei,LU Chun-shien.Distributed compressive video sensing[C]//Proceedings of 2009 IEEE International Conference on Acoustics,Speech,and Signal Processing.Taipei,Taiwan:IEEE,2009:1169-1172.
[4]Do T,Chen Yi,Nguyen D,et al.Distributed compressed video sensing[C]//Proceedings of 2009 IEEE International Conference on Image Processing.Cario,Egypt:IEEE,2009:1393-1396.
[5]Mun S,Fowler J.Residual reconstruction for block-based compressed sensing of video[C]//Proceedings of2011 Data Compression Conference.Snowbird,Utah,USA:IEEE,2011:183-192.
[6]Do T,Gan Lu,Nguyen N,etal.Fastand EfficientCompressive Sensing Using Structurally Random Matrices[J].IEEETransactions on Signal Processing,2012,60(1):139-154.
[7]Figueiredo M,Nowak R,Wrigh S.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586-597.
[8]Tropp J,Gilbert A.Signal recovery from random measurements via orthogonalmatching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[9]LICheng-bo.An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing[D].Houston:Rice University,2009.

常侃(1983—),男,广西南宁人,2010年于北京邮电大学获博士学位,现为广西大学计算机与电子信息学院副教授,主要研究方向为压缩感知、视频编码与传输;
CHANG Kan was born in Nanning,Guangxi Zhuang Autonomous Region,in 1983.He received the Ph.D.degree from Beijing University of Posts and Telecommunication in 2010,and is now an associate professor of School of Computer and Electronic Information,Guangxi University.His research interests include compressed sensing,video coding and transmission.
Email:pandack0619@163.com
覃团发(1966—),男,广西宾阳人,1997年于南京大学获博士学位,现为广西大学计算机与电子信息学院副院长、教授、中国电子学会高级会员、中国通信学会高级会员,主要研究方向为无线多媒体通信、网络编码、视频编码和图像检索;
QIN Tuan-fa was born in Binyang,Guangxi Zhuang Autonomous Region,in 1966.He received the Ph.D.degree from Nanjing University in 1997.He is now a professor and vice Dean of School of Computer and Electronic Information,GuangxiUniversity.He is also the seniormember of China Institute of Electronics and China Communications Institute.His research interests includewirelessmultimedia communications,network coding,video encoding and image retrieval.
Email:tfqin@gxu.edu.cn
唐振华(1979—),男,广西玉林人,2009年于华中科技大学获博士学位,现为广西大学计算机与电子信息学院副教授,主要研究方向为无线多媒体通信。
TANG Zhen-hua was born in Yulin,Guangxi Zhuang Autonomous Region,in 1979.He received the Ph.D.degree from Huazhong University of Science and Technology in 2009,and is now an associate professor of School of Computer and Electronic Information,Guangxi University.His research concerns wirelessmultimedia communications.
Email:tangedward@126.com
Residual Reconstruction Based Distributed Compressed Video Sensing
CHANG Kan,QIN Tuan-fa,TANG Zhen-hua
(School of Computer and Electronic Information,GuangxiUniversity,Nanning 530004,China)
To improve the performance of Distributed Compressed Video Sensing(DCVS),a residual reconstruction based DCVS framework is proposed.The proposed framework samples each video frame independently at the encoder.However,it recovers frames at the decoder by exploiting inter frame correlation.Firstly,the key frame of a Group of Pictures(GOP)is independently reconstructed.Secondly,Side Information(SI)is generated by performing bi-directional Motion Estimation(ME)and Motion Compensation(MC)through the reconstructed key frames.Afterwards,the generated SI frame is sampled by the samematrix as the one at the encoder,and the measurement of SI is used to calculate the residual ofmeasurement.Finally,total variationminimization is applied to reconstruct the residual signal,and the output frame is formed by adding SI to the residual signal.Experimental results show that compared with the existing DCVSmethod,the proposed one can getmore than 2.8 dB Peak Signal to Noise Ratio(PSNR)increment at the same sampling rate.
compressed sensing(CS);distributed compressed video sensing(DCVS);residual reconstruction;total variationminimization;side information(SI)
TN919.8
A
1001-893X(2013)03-0274-05
10.3969/j.issn.1001-893x.2013.03.009
2012-08-31;
2012-11-09 Received date:2012-08-31;Revised date:2012-11-09
❋❋通讯作者:pandack0619@163.com Corresponding author:pandack0619@163.com
国家自然科学基金资助项目(61261023);广西自然科学基金资助项目(2011GXNSFD018024);广西教育厅科研项目资助(201203YB001)
Foundation Item:The National Natural Science Foundation of China(No.61261023);The Natural Science Foundation of Guangxi(2011GXNSFD018024);The Foundation of Education Commission of Guangxi(201203YB001)

