基于干扰抑制的恒模波束跟踪新算法❋

祝俊，王 军，林文长，唐斌

（电子科技大学电子工程学院，成都611731）

基于干扰抑制的恒模波束跟踪新算法❋

祝俊❋❋，王 军，林文长，唐斌

（电子科技大学电子工程学院，成都611731）

当干扰信号强度不小于期望信号时，常规恒模算法（CMA）会错误跟踪到干扰信号；期望信号导向矢量线性约束恒模算法（LSCCMA）通过对期望信号来波方向约束，可正确跟踪到期望信号，但是算法在干扰信号来波方向上不能形成明显的零陷。为此，提出了基于干扰约束的恒模算法（LICCMBTA）。理论分析和仿真结果证明，该算法不仅可以正确跟踪到期望信号，并且可实现在多个强干扰信号来波方向上形成深度可调的干扰零陷，从而提高了常规恒模算法波束跟踪的稳健性。

波束形成；智能天线；恒模算法；波束跟踪；干扰约束；干扰零陷

1 引 言

稳健波束形成技术广泛应用于雷达、无线通信、声纳、医学成像和天文学等领域［1－3］。智能天线从空域上实现了对干扰信号的抑制，同时使期望信号无失真地传输。恒模算法（CMA）是一种性能良好的盲波束形成算法，它无需训练信号，收敛速度较快，不仅可用于恒模信号，也可用于某些非恒模信号［4－7］。但由于恒模算法这种普适特性，在干扰信号强度不小于期望信号时，它容易错误跟踪到干扰信号，这种情况称之干扰捕获问题。

针对干扰捕获问题，可以将多个恒模阵列级联或者截获所有恒模信号，然后进行进一步处理以确定所需信号［8－9］，但当入射信号较多时，算法的运算量将急剧增加，同时它不能保证同一信号始终被天线阵列所截获；也可以利用期望信号导向矢量来对恒模算法进行约束［10］，该算法的缺点是在干扰信号来波方向上不能形成明显的零陷，此外，算法还需要知道期望信号的确切的来波方向。然而在实际环境中，期望信号的方向往往是变化的，甚至变化速率很大，这将严重影响算法的跟踪性能。

本文以干扰信号导向矢量为约束条件，提出了干扰约束恒模算法（LICCMBTA），以解决干扰捕获问题。仿真表明，该算法不仅解决了干扰捕获问题，抑制了多个强干扰信号，而且不需要知道期望信号来波方向，提高了抗干扰能力，算法适用于复杂电磁环境中。

2 干扰抑制恒模算法

对于任意阵列M阵元的接收信号模型，假设阵元m的空间坐标为pm＝［xmymzm］，选择坐标原点为参考点，某平面波信号s（t）以入射方向（θ，φ）到达天线阵元，其中θ和φ分别表示入射信号的俯仰角和方位角。信号达到阵元m相对参考点的时延τm为

其中，c为光速，r为入射信号单位方向向量，则对应空间相位差为

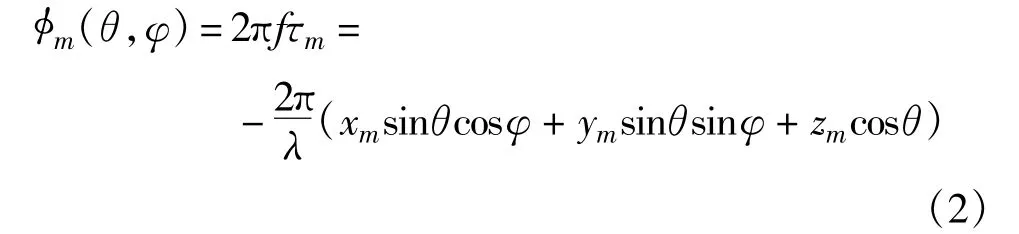
故M个阵元阵列的导向向量可以表示为

则阵列接收信号表示为

式中，υ（n）为各阵元加性高斯白噪声。

恒模算法的代价函数的一般表达式为

其中，E［·］代表统计平均，y（n）＝wH（n）x（n）代表输出信号，p、q是常数，取p＝1、q＝2。BPSK信号时，K＝1，M为阵元数。

当干扰信号和期望信号非常接近时，或者干扰信号高于期望信号时，CMA算法容易捕获到干扰信号而跟丢期望信号。为解决这一问题，构造代价函数为

其中，w是M×1权矢量，N为干扰信号个数，A＝［a1，a2，…，aN］为干扰信号导向矢量，¯ε＝［ε1，ε2，…，εN］为干扰零陷决定因子。对于式（6）的求解，运用最优化理论，显然是个条件极值问题，构造拉格朗日性能函数

其中，λ为拉格朗日乘子，对w求导可得

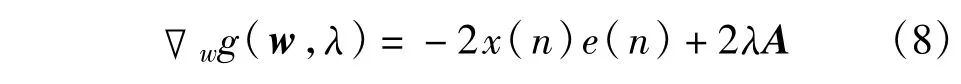
其中，误差函数

对w求解，采用最陡下降法。令

将∇wg（w）代入式（10），则有

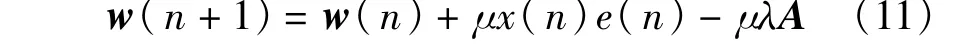
将式（11）代入到约束条件wHA＝¯ε中，得

故权向量的迭代表达式可表示为

步骤1：初始化，w＝［1，01，…，0M－1］，ε0，ε1，…，εN，μ，（θi，φi），（i＝1，…，N），设置门限值Error；

步骤2：计算α（θi，φi），y（n）＝wH（n）x（n），e（n）＝2·y（n）·abs（y（n）－M）/abs（y（n）），

步骤3：当e（n）＞Error，n＝n＋1，转到步骤2。

3 算法性能分析

3.1 输出信干比

输出信干比和计算复杂度是衡量波束形成算法优劣的主要因素，输出信干比（SIRout）定义为

其中，Rs为期望信号相关矩阵；Ri为干扰信号相关矩阵，wopt为最优权系数，Num为快拍数。定义输入干信比（ISRin）为

设Ai＝C·As，Ai表示干扰信号的幅度，As表示期望信号的幅度，则式（17）可写为

当算法收敛后，式（6）可以改写为

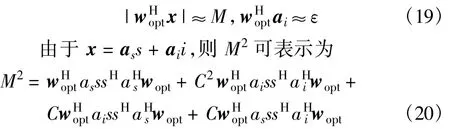
求解式（21）方程，β2可表示为）

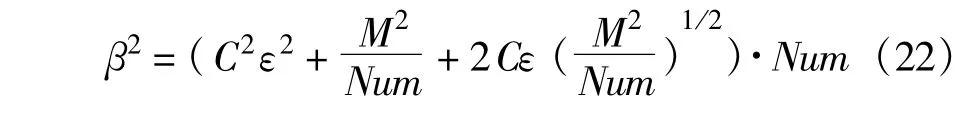
因此，代价函数可写为

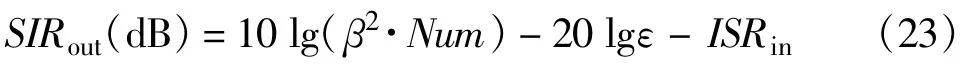
故输出信噪比的理论表达式为

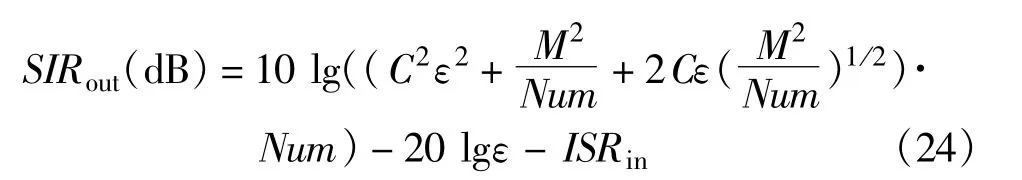
由式（24）可知，当阵元个数、采用快拍数和输入干信比一定时，输出信干比仅与ε有关。

3.2 计算复杂度

在干扰信号来波方向已知的情况下，用迭代的方法实现LICCMBTA的计算复杂度如下（M＆D代表乘法和除法，A＆S代表加法和减法）：

（1）y（n）＝wH（n）x（n），A＆S：M－1，M＆D：M；

（3）w（n＋1）＝（I－Qi）w（n）＋μ（I－Qi）x（n）e（n）＋εiai，A＆S：2M2＋

6M＋1，M＆D：2M2＋5。

用迭代方法实现CMA的计算复杂度如下：

（1）y（n）＝wH（n）x（n），A＆S：M－1，M＆D：M；

（3）w（n＋1）＝w（n）＋μx（n）e（n），A＆S：M；M＆D：M＋1。

在期望信号来波方向已知的情况下，用迭代的方法实现LSCCMA的计算复杂度如下：

（1）y（n）＝wH（n）x（n），A＆S：M－1，M＆D：M；

（3）w（n＋1）＝（I－P）w（n）＋μ（I－P）x（n）e（n）＋εas，A＆S：2M2＋6M＋1，M＆D：2M2＋5。

表1总结了3种算法的计算复杂度，可见LICCMBTA和LSCCMA具有相同的计算复杂度。

表1 计算复杂度Table 1 Computational complexity

4 仿真分析

4.1 单个干扰信号的捕获问题

设期望信号来波方向未知，干扰信号来波方向已知。4元均匀线阵，阵元间距为1/2波长，信号调制形式为BPSK，Num＝2 048，ε＝0.01。

干扰信号来波方向为40°，期望信号来波方向为10°。ISRin＝［－10 dB，10 dB］，步进为1 dB。

图1为不同ISR下SIR变化曲线，可见，当ISR小于0 dB时，输出SIR大于0 dB，且ISR越小，SIR越大，即对干扰的抑制越明显；当ISR大于0 dB时，输出SIR小于0 dB，且ISR越大，SIR越小，结合图2归一化方向图，表明当干扰信号的强度大于期望信号（ISR＝5 dB）及干扰信号与所需信号的调制方式（BPSK）相同时，CMA存在干扰捕获问题。

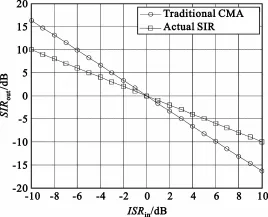
图1 不同ISR下SIR变化曲线

图2 不同ISR情况下的归一化方向图

利用LICCMBTA算法再次仿真，假设干扰信号来波方向为－30°，期望信号来波方向为5°。仿真结果如图3～6所示。

图3 不同ISR下SIR变化曲线

从图3可见LICCMBTA算法的SIRout比LSCCMA算法高40 dB。

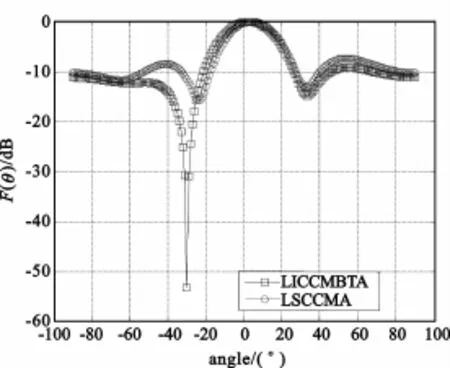
图4 不同ISR情况下的归一化方向图

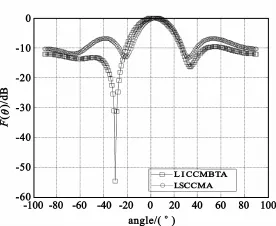
图5 不同算法下的归一化方向图

图6 不同算法下的归一化方向图

从图4～6可见，在干扰方向上，LICCMBTA能够形成很深的零陷，而其他算法则形成不了这么深的零陷，零陷的深度可以通过输出信干比的决定因子ε来调整。

4.2 多个干扰信号的捕获问题

LICCMBTA在干扰信号个数为3的情况下干扰捕获问题，假设信号方向为10°，干扰信号方向分别为－30°、30°和50°，仿真结果如图7～8所示。

图7 不同ISR下SIR变化曲线

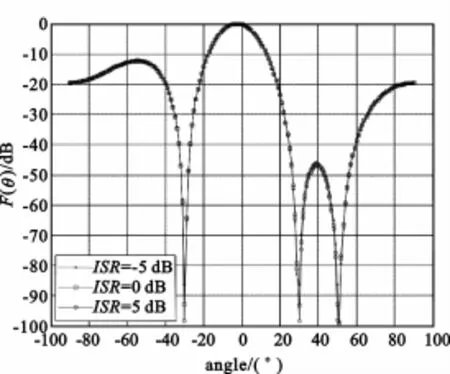
图8 不同ISR下的归一化方向图

图7和图8表明，干扰数在自由度范围内时，LICCMBTA仍可以解决干扰捕获问题，而且在各个干扰方向上形成明显的零陷，有效地抑制了干扰。不足之处在于，方向图最强处没有对准所需信号来波方向，有一定的偏移，但是还在3 dB波束宽度内。

4.3 计算复杂度

仿真条件同4.2节，仿真结果如图9所示。由图9可知，由于基于干扰约束的恒模算法增加了干扰方向约束条件，因而计算量较常规恒模算法大，符合表1算法的计算复杂度分析。

图9 权向量和迭代次数之间关系

5 结束语

本文提出了以干扰导向矢量作为权矢量约束条件的LICCMBTA，以解决CMA的干扰捕获问题，而且在多个干扰方向上形成零陷，应用最优化原理推导出了该算法的迭代过程。理论分析和仿真结果证明了在相同计算复杂度下，较LSCCMA算法不仅可以解决CMA干扰捕获问题，而且可在干扰信号来波方向上形成了明显的可调深度干扰零陷，有效抑制了干扰信号，在工程上具有很好的实用价值。

［1］Vorobyov SA，Gershman A B，Luo ZQ.Robust adaptive beamforming using worst-case performance optimization：A solution to the signalmismatch problem［J］.IEEE Transactions on Signal Processing，2003，51（2）：313－324.

［2］Wang Y C，Wang X，Liu HW，et al.On the Design of Constant Modulus Probing Signals for MIMORadar［J］.IEEE Transactions on Signal Processing，2012，60（8）：4432－4438.

［3］Li J，Stoica P，Wang Z.On robust Capon beamforming and diagonal loading［J］.IEEE Transactions on Signal Processing，2003，51（7）：1702－1715.

［4］王丽娜，王兵.一种新的卫星智能天线自适应波束形成算法［J］.电讯技术，2009，49（4）：1－5.WANG Li-na，WANG Bing.A Novel Adaptive Beamforming Algorithm for Smart Antennas in Satellite Systems［J］.Telecommunication Engineering，2009，49（4）：1－5.（in Chinese）

［5］谢泽明，林武呈，刘樟华.恒模数字波束形成器在多天线软件无线电平台中的实现［J］.电讯技术，2008，48（1）：37－40.XIE Ze-ming，LINWu-cheng，LIU Zhang-hua.Implementation of DBF Based on CMA in the Multi-antenna SDR Platform［J］.Telecommunication Engineering，2008，48（1）：37－40.（in Chinese）

［6］Cai Y L，De L，Rodrigo C，et al.Low－Complexity Variable Forgetting Factor Mechanism for Blind Adaptive Constrained ConstantModulus Algorithms［J］.IEEE Transactions on Signal Processing，2012，60（8）：3988－4002.

［7］Keerthi A，Mathur A，Shynk J.Misadjustment and tracking analysis of the constantmodulus array［J］.IEEE Transactions on Signal Processing，1998，46（1）：51－58.

［8］Song X，Wang JK，LiQM，etal.Robust Least Squares Constant Modulus Algorithm to Signal Steering Vector Mismatches［J］.Wireless Personal Communications，2013，68（1）：79－94.

［9］Shynk J，Gooch R.The constantmodulusarray for cochannel signal copy and direction finding［J］.IEEE Transactions on Signal Processing，1996，44（3）：652－660.

［10］Xu C，Feng G，Kwak K S.Amodified constrained constantmodulusapproach to blind adaptive multiuser detection［J］.IEEE Transactions on Communications，2001，49（9）：1642－1648.

祝俊（1974—），男，四川蓬安人，博士，在站博士后，主要从事电子对抗方面的研究。

ZHU Jun was born in Peng′an，Sichuan Province，in 1974.He is a postdoctoral fellow in Postdoctoral Research Station of Electronic Science and Technology at University of Electronic Science and Technology of China.His research concerns electronic countermeasure.

Email：uestczhujun＠163.com

王军（1971—），男，甘肃兰州人，高级工程师，主要从事电子对抗方面的研究；

WANG Jun was born in Lanzhou，Gangsu Province，in 1971.He is now a senior engineer.His research concerns electronic countermeasure.

Email：wangjun＠ee.uestc.edu.cn

林文长（1985—），男，福建龙岩人，硕士研究生，主要研究方向为阵列信号处理；

LIN Wen-chang was born in Longyan，Fujiang Province，in 1985.He is now a graduate student.His research concerns array signal processing.

Email：linwc163＠126.com

唐斌（1964—），男，四川广安人，教授、博士生导师，主要从事电子对抗、雷达抗干扰和新一代通信技术方面的研究。

TANG Bin wasborn in Guang′an，Sichuan Province，in 1964.He is now a professor and also the Ph.D.supervisor.His research interests include electronic countermeasure，radar anti-jamming technology and new-generation communication technology.

Email：bint＠ee.uestc.edu.cn

A New Constant M odulus Beam Tracking Algorithm Based on Interference Signals Constrained

ZHU Jun，WANG Jun，LINWen-chang，TANG Bin
（School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

The traditional constantmodulus algorithm（CMA）fails to track the desired signal，when it companies with stronger interference signals.Though the linear signals constrained constantmodulus algorithm（LSCCMA）can solve the problem when knowing the accurate direction of arrival（DOA）of the desired signal，it cannot form an obvious interference null at the DOA of interference signals.Therefore，a linear interference constantmodulus beam tracking algorithm（LICCMBTA）is presented in this paper based on abovementioned problems.Theoretical analysis and simulation results indicate that the LICCMBTA can not only track the desired signal correctly，but also forms deep null at the DOA of interference signals simultaneously according to the adjustable null factors.The LICCMBTA improves the robustness of the traditional CMA.

beamforming；smartantenna；constantmodulus algorithm（CMA）；beam tracking；interference constraints；interference null

TN911.72

A

1001－893X（2013）03－0269－05

10.3969/j.issn.1001－893x.2013.03.008

2012－12－04；

2013－03－18 Received date：2012－12－04；Revised date：2013－03－18

❋❋通讯作者：uestczhujun＠163.com Corresponding author：uestczhujun＠163.com