一种新的跳频信号时延估计方法❋

闫云斌，全厚德，崔佩璋

（军械工程学院信息工程系，石家庄050003）

一种新的跳频信号时延估计方法❋

闫云斌❋❋，全厚德，崔佩璋

（军械工程学院信息工程系，石家庄050003）

针对噪声环境下的跳频信号，提出了一种基于稀疏分解的时延估计方法。对跳频信号采用稀疏分解重构进行了研究，在此基础上，在不同天线下对跳频信号分别进行重构，得到每跳信号对应的载波频率和时间中心，从而估计出跳频信号的时延。仿真结果表明，在信噪比大于7 dB时，跳频信号的时延估计误差基本趋近于零，验证了时延估计方法的有效性。

跳频信号；稀疏分解；时延估计；信号重构

1 引 言

跳频通信因其良好的抗干扰性、低截获概率及组网能力，在战术通信中得到了广泛的应用。一般跳频信号的载波可以按照预先设定的频表随机跳变，从而有效地躲避敌方的干扰。而这种跳变的机制导致目前一些信号处理方法对跳频信号越来越力不从心，尤其是针对跳频信号时延估计技术存在很大的难题。而对跳频信号进行时延估计，不仅有利于传统的测向、定位跟踪以及干扰，而且如果作为合作方通信，通过估计观测时间内每跳信号的时间延迟，可以作为判断跳频信号是否存在跟踪干扰的特征值之一。因此，跳频信号的时延估计在军事上具有重要的意义和广阔的应用前景。

目前，时延估计主要采用传统的估计方法［1］、基于信号建模［2］和自适应［3］等方法，这些方法在线性条件下能得到很好的估计性能，但是却不适于宽带信号及低信噪比的条件。跳频信号是一种典型的非平稳信号，而对于噪声环境下的非平稳信号，文献［4］采用时频联合分析的方法，采用短时傅里叶谱图的瞬时频域相关法实现了对时延的估计，但是对于频率随时间非线性变化的单分量信号或者多分量信号，该方法会出现严重的交叉项干扰［5］。文献［6］则提出了一种基于循环互相关的时延估计方法，能够很好地处理具有周期平稳特性的信号。而跳频信号在实验的时间范围内不具有周期的平稳特性，因此上述方法不适用于跳频信号的时延估计。

近几年来，随着稀疏分解理论的逐步完善，其在信号处理领域的优势逐渐体现出来。稀疏分解的主要目的是从一个过完备的矢量集（或函数集）中选择尽量少的元素来表示已知信号。由于稀疏分解不仅能够得到信号精确的时频分布，而且不会产生交叉项干扰，所以被广泛应用于多分量信号的时频分析和参数估计［7－8］。跳频信号恰好可以看成多个信号分量的线性组合，因此可以采用稀疏分解对跳频信号进行时频分析［9］。

本文通过对跳频信号模型的稀疏性进行分析，提出了一种基于稀疏分解的跳频信号时延估计方法，该方法依据跳频信号的特点，构建了一组时频原子词典，应用推广的正则化FOCUSS算法［11］在噪声环境下，分别从天线1和2的接收端得到的跳频信号进行重构，获得相对应载波频率上每跳信号的时间中心，从而得到每跳的时间延迟，最后通过仿真验证了该时延估计方法的有效性。

2 时延估计的信号模型

假设接收端从天线1和2上接收到的跳频信号分别记为

式中，x0（t）为主天线上接收到的跳频信号；x1（t）为对应的辅天线上接收到的跳频信号；n0（t）和n1（t）为加性高斯白噪声，其中噪声功率为σ2；s（t）为接收端在观测时间内得到的跳频信号。

跳频信号是一类载频在伪随机序列控制下随时间变化的非平稳信号，在接收端，假设观察时间T内，跳频接收机共接收到M跳信号，则接收到的信号可以表示为

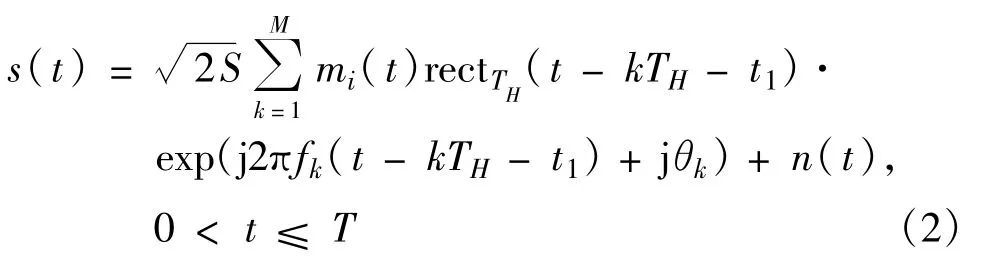
其中，S为信号功率，mi（t）是经过基带调制的传输数据，fk和θk是第k跳的载波频率和相位，TH是跳频信号驻留时间，而M为观测时间内产生的跳频频点数，n（t）为高斯白噪声，rectTH为宽度为TH的矩形窗。

式中，t1是第一个跳变时刻，则第k个跳变时刻为t1＋（k－1）TH。

由于在时延估计过程中只考虑时延参数τ，因此跳频信号接收端模型可以简化。令跳频信号的幅度为1，即此时

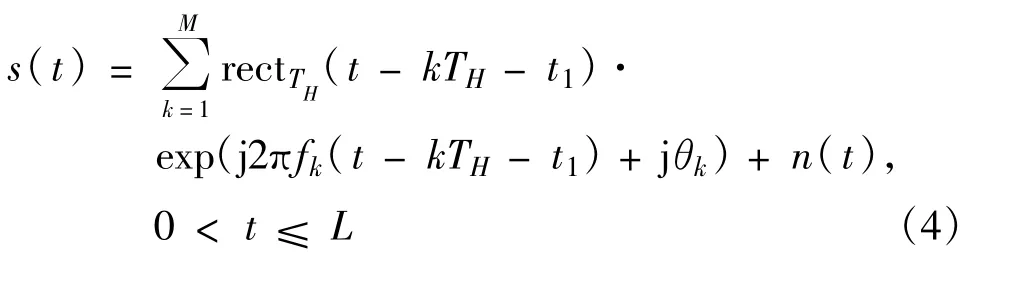
3 基于稀疏分解的跳频信号时延估计算法

3.1 跳频信号时延估计算法

基于稀疏分解的跳频信号时延估计框架如图1所示。接收端从天线1和2获得的跳频信号首先经过接收机射频滤波器后，分别对得到的信号进行稀疏分解，完成跳频信号的重构，获得相对应的跳频信号载波频率和对应的时间中心T0（k）和T1（k），k＝1，2，…，M，其中时间延迟为两时间中心之差，即τ（k）＝T1（k）－T0（k），这样就估计得到了观测时间T内M跳信号的时延。因此，对跳频信号时延估计的关键是对跳频信号的重构。为了形象地说明跳频信号的时延估计，图2给出了接收端接收到的跳频信号和时延信号的时域波形图，从图中可以直观地看出，这两路信号的时延可表示为两信号对应的时间中心之差。

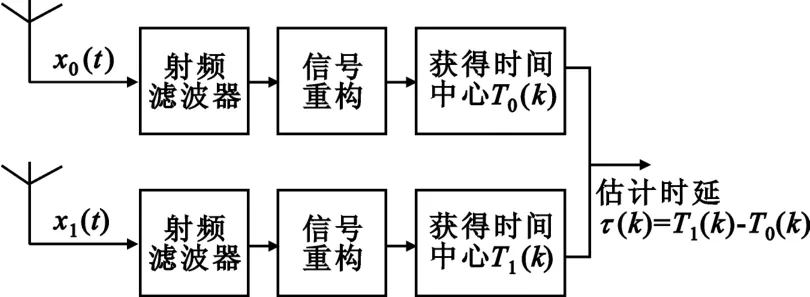
图1 基于稀疏分解的跳频信号时延估计框图

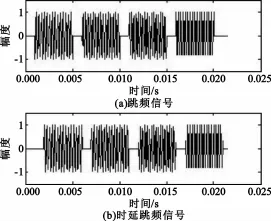
图2 跳频信号和时延信号的时域波形

3.2 跳频信号稀疏性分析和重构

跳频信号的每一跳可以看成是时域不重叠的有限长的正弦信号［9］，因此在接收端收到的信号在某段观测时间内可以看成是时域不重叠有限长正弦信号的线性叠加。在信号的稀疏分解中，原子的选取、字典的构造、求解算法的设计3个问题是利用稀疏分解求解的关键。其中字典的构造一般情况下应满足字典与信号是自适应的，换句话说字典一般是从信号中学习得到的，因此应该根据信号的先验信息及实际需要设计字典。

跳频信号的重构实质上由3个参数决定，时间中心Tk、载波频率fk和跳频信号驻留时间TH，由于本文研究的范围属于合作方通信，因此对于跳频信号的持续时间是已知的。本文为了更好地实现跳频信号的重构，根据跳频信号的特点选取信号单位能量的加窗正弦函数作为过完备库中的原子，如下式所示：

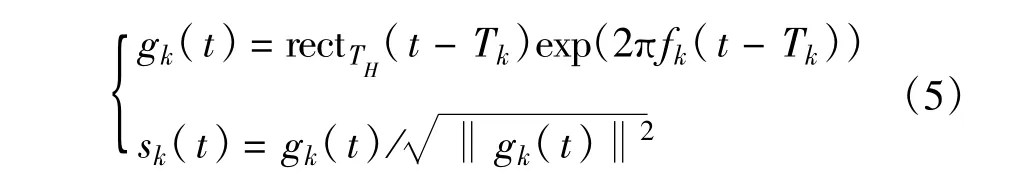
式中，fk表示正弦函数对应的频率，其取值为跳频信号所处的频段内所有的跳频频点，假设所有跳频频点数为Nf，Tk为对应的第k跳信号的时间中心，其中Tk∈［0，TH/2］，实际中可以按照需要的精度均匀取值k＝1，2，…，Nt。原子库中原子的个数为M＝Nf·Nt，根据式（6）扩展构建如下的稀疏基：

假设αk为第k跳信号对应的复包络，记α如下式所示：

当某段观测时间T内没有该跳信号时αk＝0。由于在T内跳频信号出现的次数仅是很小一部分，所以α中非零元素个数K远远小于原子库中原子的个数M。

那么，式（4）可以描述为

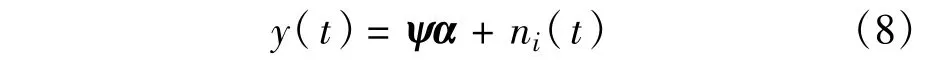
依据稀疏分解理论，由跳频信号接收端采样信号估计稀疏系数α的问题即转化为一般的信号稀疏分解问题，根据式（8），通过采样获得测量值y（t）后，应用推广的正则化FOCUSS算法［10］估计该稀疏表示系数。基于稀疏分解的跳频信号时延估计步骤如下：

步骤1：分别对不同天线上接收到的跳频信号依据跳频信号的特点，依据式（5）构建过完备库中的原子；

步骤2：根据跳频信号所在频段和频率间隔等实际需求信息，依据步骤1选取的载波频率原子单元sk（t），利用式（6）构建跳频信号重构的冗余基

步骤4：通过对两路跳频信号分别分解得到包络稀疏表示系数α，对应α中的非零分量，求出跳频载波频率和时间中心，在相对应的跳频频点上，两者时间中心之差即为该跳信号上对应的时间延迟。

4 仿真结果及分析

为了验证基于稀疏分解的跳频信号时延估计方法的有效性，本文在仿真过程中，假设天线接收到的跳频信号属于超短波频段，设置工作频段为30～88 MHz，其中频率间隔为25 kHz，共有2 320个跳频频点，跳速为200 hop/s，跳频周期为0.005 s，其中跳频驻留时间为0.004 s，换频时间为0.001 s。在观测时间内接收端从天线1和2上分别接收到4跳完整的信号，其中跳频信号样本的跳频频率分别为35 MHz、37.5 MHz、42.5 MHz和40 MHz。两路跳频信号中对应的跳频频点上的时间延迟量均为1ms。在仿真过程中，由于跳频工作的频率很高，在兆赫数量级上，仿真时采样频率要达到200 MHz以上，因此本文在仿真过程中，在不对仿真结果产生影响的基础上，适当把载波频率和跳频点的频率等比例降低到千赫数量级上，可以提高仿真速度。此时设定接收到的跳频信号幅度为1，采样频率为200 kHz。噪声采用零均值的高斯白噪声，在噪声存在情况下，正则化参数的选择和信噪比有关，具体的值可以根据L－曲线准则估计出［11］。

在仿真过程中，本文分别用基追踪算法和推广的正则化FOCUSS算法，对接收到的跳频信号的时延进行了估计，为此定义了时延估计的归一化估计误差如下：其中，t′i为跳频信号估计的第i跳的时间中心值，ti为跳频信号实际第i跳的时间中心值。在此基础上，分析跳频信号时延估计性能。

在估计过程中，当信噪比小于0 dB时，噪声已经完全淹没信号，信号的特征完全消失，时延估计算法不能实现。当信噪比SNR从0 dB到25 dB以1 dB为步进变化时，接收端得到的跳频信号在同一信噪比下经过100次Monte Carlo仿真实验，计算每次接收端跳频信号时延估计误差并取平均值。

图3给出了不同信噪比下跳频信号的时延估计性能。从图中可以看出，当信噪比在0～7 dB时，随着信噪比的增加，采用推广的FOCUSS算法和基追踪算法下的跳频信号时延估计误差都在减小。当信噪比在7 dB以上时，采用推广的正则化FOCUSS算法其跳频信号时延估计误差基本趋近于零，而采用基追踪算法下时延估计误差保持在2左右，其主要原因是由于基追踪算法对跳频信号分解不完整，会出现丢失跳频频点的现象。

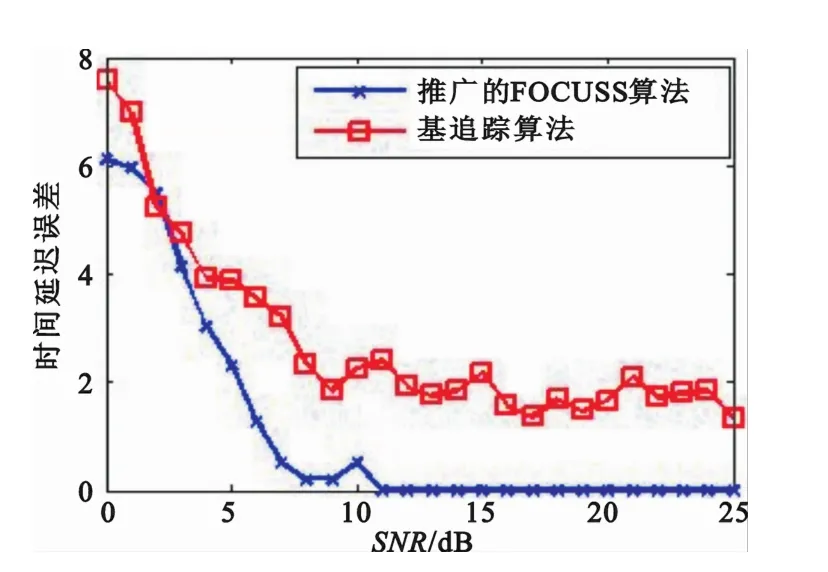
图3 时延估计在不同信噪比下归一化重构误差

保持上面的仿真参数不变，改变观测时间内接收到的跳频频点数，图4给出了观测时间内接收到的跳频信号分别为4跳和8跳的情况下，采用推广的正则化FOCUSS算法，在不同信噪比情况下，时间延迟的归一化估计误差。从图中可以看出，随着信噪比的增加，估计误差都在逐渐减小。而在观测时间T内跳频频点为8跳时，在信噪比在7 dB以下时，其重构误差略大于跳频频点为4跳的情况，而在信噪比大于7 dB时，估计误差均趋近于零，能够实现对跳频信号时延几乎无误的估计。因此可知，该时延估计算法对接收端一次处理的跳频点数较多时，在信噪比为7 dB以上时，时延估计精度几乎没有影响。

图4 观测时间内含不同跳频频点下时延估计归一化重构误差

5 结论

本文将稀疏分解理论应用到跳频信号的时延估计中，分别对天线1和2的接收端获得的跳频信号利用稀疏分解进行重构，得到了每跳信号对应的时间中心，从而得到跳频信号在相同跳频频点上的时延。仿真结果表明，在噪声环境下，选择合适的正则参数，跳频信号在信噪比大于7 dB时可以对跳频信号的时延实现几乎无误的估计；在观测时间内，跳频频点的增加对时延估计性能影响不大。本文提出的跳频时延估计算法，对于跳频频点数量较少时跳频信号的时延估计具有明显优势，而且采用了稀疏分解理论，与传统时频分析比较，不存在交叉干扰的影响，因此具有广泛的应用空间。但是本文提出的时延估计方法主要在高斯白噪声环境下，下一步将会对有色噪声和干扰环境下的跳频信号时延估计方法进行研究。

［1］黎英云.微弱多径信号时延估计技术研究［D］.武汉：华中科技大学，2009.LIYing-yun.Research on Time Delay Estimation Technology ofWeak Multipath Signal［D］.Wuhan：Huazhong University of Science and Technology，2009.（in Chinese）

［2］Cabasson A，Meste O.Time Delay Estimation：A New Insight Into the Woody′s Method［J］.IEEE Signal Processing Letters，2008，15（6）：573－576.

［3］Emadzadeh A A，Lopes CG，Speyer JL.Online Time Delay Estimation of Pulsar Signals for Relative Navigation using Adaptive Filters［C］//Proceedings of 2008 IEEE/ION Position，Location and Navigation Symposium.Monterey，CA：IEEE，2008：714－719.

［4］字正华，石庚辰.基于短时傅立叶变换谱图的非平稳信号时延估计方法［J］.探测与控制学报，2007，29（6）：19－23.ZIZheng-hua，SHIGeng-chen.The Time-delay estimation algorithm for non-stationary signal based on short-timeFourier transform（STFT）spectrogram［J］.Journal of Detection＆Control，2007，29（6）：19－23.（in Chinese）

［5］Barbarossa S，Scagllone A.Parameter estimation of spread spectrum frequency hopping signals using time-frequency distributable［C］//Proceedings of First IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communication.Paris，France：IEEE，1997：213－216.

［6］史建锋，王可人.基于循环互相关的LFM信号时延估计及性能分析［J］.现代雷达，2007，29（4）：53－56.SHIJian-feng，WANG Ke-ren.Time-delay estimation of LFM signal and its performance analysis based on cyclic cross-correlation［J］.Modern Radar，2007，29（4）：53－56.（in Chinese）

［7］Buhan A.A Four Parameter Atomic Decomposition of Chillets［J］.IEEE Transactions on Signal Processing，1999，47（3）：731－745.

［8］Lopez-Risueno G，Grajal J，Yeste-Ojeda O.Atomic decomposition-based radar complex signal interception［J］.IEE Proceedings-Radar Sonar Navigation，2003，150（4）：323－331.

［9］范海宁，郭英.一种新的跳频信号参数盲估计算法［J］.信号处理，2009，25（11）：1754－1759.FAN Hai-ning，GUO Ying.A novel blind parameter estimationalgorithm of frequency-hopping signals［J］.Signal Processing，2009，25（11）：1754－1759.（in Chinese）

［10］杜小勇，胡卫东，郁文贤.推广正则化FOCUSS算法及收敛性分析［J］.系统工程与电子技术，2005，27（5）：922－925.DU Xiao-yong，HU Wei-dong，YU Wen-xian.Generalized regularized FOCUSS algorithm and its convergence analysis［J］.Systems Engineering and Electronics，2005，27（5）：922－925.（in Chinese）

［11］Johnston P R，Gulrajani R M.Selecting the corner in the L-curve approach to Tikhonov regularization［J］.IEEE Transactions on Biomedical Engineering，2000，47（9）：1293－1296.

闫云斌（1984—），男，山西朔州人，2009年获硕士学位，现为博士研究生，主要研究方向为跳频电台通信性能测试；

YAN Yun-bin was born in Shuozhou，Shanxi Province，in 1984.He received the M.S.degree in 2009.He is currentlyworking toward the Ph.D.degree.His research concernswireless communication performance test.

Email：zkjysyyb＠163.com

全厚德（1963—），男，辽宁大连人，博士，教授、博士生导师，主要研究方向为通信设备性能测试。

QUAN Hou-dewas born in Dalian，Liaoning Province，in 1963.He is now a professor with the Ph.D.degree and also the Ph.D.supervisor.His research concerns performance test of communication equipment.

A Novel Time Delay Estimation Method of Frequency-Hopping Signals

YAN Yun-bin，QUAN Hou-de，CUIPei-zhang
（Information Engineering Department，Ordnance Engineering College，Shijiazhuang 050003，China）

For frequency-hopping（FH）signal，a novelmethod of time delay estimation（TDE）is presented in the noise environment.The FH signals are reconstructed by using themethod of sparse decomposition，then，the TDE of the same hop is estimated through the carrierwave and time center of each hop which are obtained when the FH signals are reconstructed in the differentantenna respectively.Simulation results demonstrate that the error estimation is near zero when the SNR is greater than 7 dB，so the TDEmethod is effective.

frequency-hopping signal；sparse decomposition；time delay estimation；signal reconstruction

TN911.7

A

1001－893X（2013）03－0288－05

10.3969/j.issn.1001－893x.2013.03.012

2012－09－07；

2012－12－20 Received date：2012－09－07；Revised date：2012－12－20

❋❋通讯作者：zkjysyyb＠163.com Corresponding author：zkjysyyb＠163.com

总装备部科研项目

Foundation Item：Scientific Research Project of PLA General Armarment Department