部分变换半群的奇异部分的自同态

黄丽丽，杨秀良

（杭州师范大学理学院，浙江杭州310036）

0 引 言

设X＝｛1，2，…，n｝是一个有限集合，且α，β均为X上的部分变换．定义α·β如下：对任意的t∈X，都有α·β（t）＝α（β（t））．为简化记法，可将α·β记作αβ．易见，α·β也是X上的一个部分变换．

定义在X上的所有置换构成的集合在变换的复合运算下形成群，称这个群为X的置换群．则是由中所有不可逆变换构成的子半群，并称为的奇异部分．奇怪的是，至今没有人讨论的自同态．本文将通过对自同态核的讨论来填补这一空白．

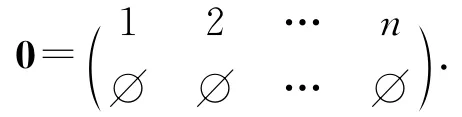
则0x是的一个常值变换．

当n≠4时，置换群有且仅有3个正规子群：自身，交错子群，以及由恒等变换构成的平凡子群．但是当n＝4时，除上述正规子群外，还有一个正规子群，称作Klein四元群．对任意的k≤n－1，定义集合如下：

任取i∈｛1，2，…，n－1｝，且对任意一个正规子群，在上定义同余≡如下：

（i）若rank（ζ）＜i，则ζ≡η当且仅当rank（η）＜i；

（ii）若rank（ζ）＞i，则ζ≡η当且仅当ζ＝η；

（iii）若rank（ζ）＝i，则ζ≡η当且仅当，且当ζ，η具有以下形式时，有

其中Bi＋1＝X＼dom（ζ）．特别地，上的任意一个同余要么是泛同余，要么具备形式，其中，1≤i≤n－1（文献［3］，Theorem 6．3．10）．

1 主要结果

则Λπ是的一个自同构．

（E1）任取，且ε为幂等元．定义如下：

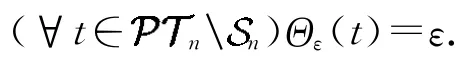
（E2）任取．定义επ：如下：任取，有

则επ是的一个自同态．

2 定理证明

定理的证明 当n＝1时，有且仅有一个自同态，即为恒等自同构．故具备形式（A）．接下来讨论当n≥2时的情况．

设φ∈End．则ker（φ）是上的一个同余．故，或ker（φ）＝≡，其中，1≤k≤n－1．

下面分情况讨论：

Case 2． 设ker（φ）＝≡，其中．则由≡的定义可知，ker（φ）＝ιn＼n．故φ为单射，从而φ∈Aut．而，故的所有自同构均为内自同构．从而φ具备形式（A）．

Case 3． 设ker（φ）＝≡，其中，1＜k≤n－1．则是ker（φ）的一个同余类．故可设｛τ｝，其中为幂等元，且rank（τ）＝i，0≤i≤n－1．

为讨论此情况，先叙述下面引理．

任取t∈｛1，2，…，n－1｝．设集合Xt＝｛ΔA：A⊂X，｜A｜＝t｝，则Xt是由的所有幂等元构成的集合．故｜Xt｜＝．

引理1 任取ε1≠ε2∈Xt，则ε1ε2＝．

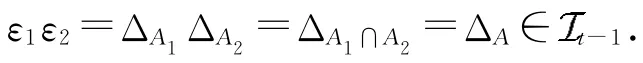
同理可得ε2ε1＝ΔA．从而ε1ε2＝．□

引理2 设φ∈End，且ker（φ）＝≡，其中，1＜k≤n－1．令＝｛λ｝，其中为幂等元．则φ（Xk）是由中的个幂等元构成的集合，且对任意的，都有αβ＝βα＝λ．

任取α≠β∈φ（Xk），则存在γ≠δ∈Xk，使得α＝φ（γ），β＝φ（δ）．由引理1可知，．故

αβ＝φ（γ）φ（δ）＝φ（γδ）＝λ，βα＝φ（δ）φ（γ）＝φ（δγ）＝λ．

从而αβ＝βα＝λ．

有了以上引理作为理论依据，接下来继续对Case3进行讨论：

任取α∈φ（Xk），则存在β∈Xk，使得α＝φ（β）．任取，则τ＝φ（γ），且．故可得

ατ＝φ（β）φ（γ）＝φ（βγ）＝τ，τα＝φ（γ）φ（β）＝φ（γβ）＝τ．

即ατ＝τα＝τ．

任取δ≠σ∈φ（Xk），则im（τ）⊂im（δ），且im（τ）⊂im（σ）．不妨令＝im（δ）＼im（τ），＝im（σ）＼im（τ）．则．（否则，存在x∈X，使得．由引理2可知，δ，σ均为幂等元，故δ（x）＝σ（x）＝x．又由引理2知，δσ＝τ．故τ（x）＝δσ（x）＝δ（x）＝x，即x∈im（τ）．矛盾．）因，且，故中至多含有个不相交的元．从而而由引理2可知，故

Subcase 3．1 设1＜k＜n－1．则，故．此不等式无解．从而此情况不成立．

Subcase 3．2 设k＝n－1．则，故．解此不等式可得：i＝0，x＝1．也即，．

任取ε∈Xn－1．不妨设，其中，｛i｝＝X＼dom（ε），故｛i｝′＝dom（ε）．因，故可设im（φ（ε））＝｛ji｝，其中ji∈X．现定义π：XX如下：

（∀i∈X）π（i）＝ji．

则π为X上的双变换．

当｜dom（α）｜＝n时，存在i≠j∈X，使得α（i）＝α（j）．不妨设p∉im（α）．设A≠B⊂X，且｜A｜＝｜B｜＝n－1，则当且仅当B＝｛p｝′，并且A∈｛｛i｝′，｛j｝′｝．故φ（ΔBαΔA）≠0当且仅当φ（ΔB）＝aπ（p），并且．又

从而φ（ΔB）φ（α）φ（ΔA）≠0当且仅当φ（ΔB）＝aπ（p），并且φ（ΔA）∈｛aπ（i），aπ（j）｝．故φ（α）＝｛π（i），π（j）｝×．

Case 4． 设n＝5．此时除上述情况外，还有一个正规子群．当时，共包含ker（φ）的450个同余类．则＝450．而＝155＜450．这与相矛盾．故此情况不成立．

综上所述，定理得证．

［1］Schreier J．Über Abbildungen einer abstrakten menge aufihre teilmengen［J］．Fund Math，1937，28：261－264．

［2］Schein B M，Teclezghi B．Endomorphisms of symmetric semigroups of functions on a finite set［J］．Comm Algebra，1998，26（12）：3921－3938．

［3］Ganyushkin O，Mazorchuk V．Introduction to classical finite transformation semigroups［M］．London：Springer Verlag，2009．