硅微阵列陀螺仪的信号滤波技术

张印强 吉训生 王寿荣

(1东南大学微惯性仪表与先进导航技术教育部重点实验室, 南京210096)

(2南京工业大学自动化与电气工程学院, 南京210009)

(3江南大学通信与控制工程学院, 无锡214122)

伴随着微机械技术的发展,硅微陀螺在汽车、惯性导航和消费电子等领域得到了广泛的应用,但受限于目前的设计和加工水平,硅微陀螺的精度和稳定性还比较低,因此,提高硅微陀螺的精度成为研究的重点和难点.

硅微陀螺的信号往往伴有大量的噪声,降低陀螺漂移误差, 尤其是随机漂移误差, 成为提高精度的关键[1].一般可以采用结构及工艺改进、测控电路改进及误差补偿和漂移信号处理[2-4]等方法来提高硅微陀螺的精度.与国内外常用的高斯-马尔科夫模型、支持向量机模型和神经网络等漂移信号处理模型[5]相比,基于集成化制造技术和数据融合技术的硅微陀螺阵列[6-7]的研究方法所建立的多个陀螺冗余检测的漂移误差模型,能够有效地提高测量性能.

本文对单芯片集成硅微阵列陀螺仪的信号滤波进行了研究.首先,对硅微阵列陀螺仪的结构设计进行了分析;然后,利用Allan方差方法建立了系统随机漂移的误差模型,利用信号差分技术建立了状态方程和观测方程，利用角速度动态跟踪技术和粒子滤波技术建立了动态滤波器;最后,通过实验分析,验证了模型的正确性.

1 硅微阵列陀螺仪的结构设计

硅微阵列陀螺仪由2个双质量双线振动陀螺仪组合而成,具有四质量块结构,同时采用折叠梁来实现解耦设计.硅微阵列陀螺仪由锚点、电极、驱动梳齿、驱动梳齿架、检测梳齿、质量块和支承梁等组成(见图1).锚点固定键合在玻璃基底上,通过横梁和直梁与驱动梳齿架连接.驱动梳齿架的两边均设计有驱动梳齿和电极,用于驱动质量块振动.驱动梳齿架与检测质量块之间通过4个折叠梁进行连接;驱动梳齿电容采用变重叠面积方式,可提高品质因数,增加灵敏度.检测质量块的可动梳齿与固定检测梳齿构成变间距的差分电容.图2为硅微阵列陀螺仪样机在显微镜下的整体和局部视图.

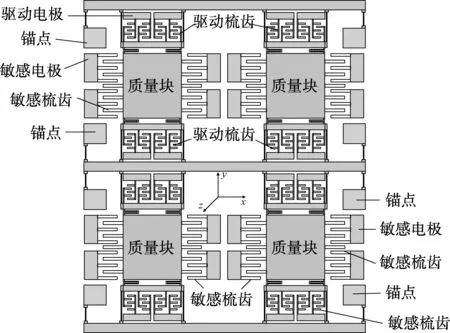
图1 硅微阵列陀螺仪的结构图

图2 硅微阵列陀螺仪样机的显微镜视图

2 硅微阵列陀螺仪的随机误差建模与分析

2.1 硅微阵列陀螺仪的随机漂移误差模型

硅微陀螺的随机漂移信号可用带噪模型[8]进行描述,即

(1)

式中,ω为被测角速度;n为角度随机游走噪声;b为陀螺漂移,其一阶导数为速率随机游走白噪声nb.

设硅微阵列陀螺仪中每个陀螺的测量结果为yi,ni为对应的角度随机游走噪声,bi为相应的陀螺漂移,nbi为各自的速率随机游走噪声,i=1,2,3,4.则误差模型可以用矩阵形式表示,即

Y=B+I·ω+V

(2)

式中

2.2 Allan方差分析

为了识别漂移数据中各噪声项的来源,采用Allan方差[9]进行误差分析.

设数据的样本长度为N,采样周期为T.将样本分成k组,每组含m个样本点,则每组的相关时间τ=mT,通过求平均得到新的样本序列，即

(3)

(4)

式中,〈·〉为总体平均.

采用Allan方差对硅微阵列陀螺仪的零漂信号进行分析，结果如图3和表1所示.由Allan方差分析结果可以看出，零漂1的各误差项都比较大,零漂4的零偏不稳定性接近零漂1,而零漂2和零漂3的零偏不稳定性相对较小.

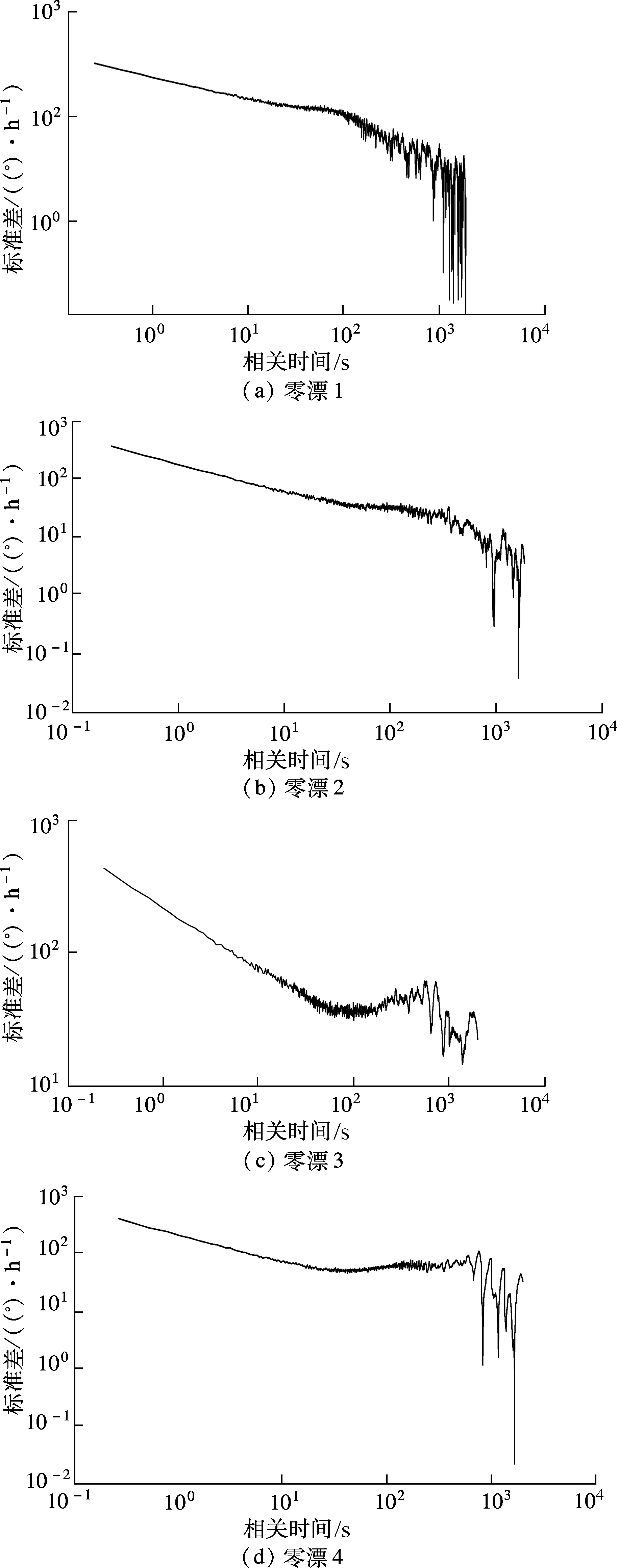
图3 硅微阵列陀螺仪零漂信号的Allan方差曲线

表1 Allan方差噪声系数的分析结果

3 硅微阵列陀螺仪的动态滤波器设计

3.1 动态滤波器的模型结构

硅微阵列陀螺仪动态滤波器由数据融合滤波器和角速度跟踪滤波器构成，如图4所示.

图4 硅微阵列陀螺仪的动态滤波器结构

数据融合滤波器对硅微阵列陀螺仪的测量信号进行滤波处理以减小随机漂移误差;角速度跟踪滤波器进行第二级滤波处理,得到较为准确的动态角速度输出信号.

3.2 数据融合滤波器

在动态滤波时,由于陀螺阵列中单个陀螺仪敏感的角速度相同,利用信号差分技术可得到漂移信息,进而可利用随机误差模型对速率随机游走噪声nb进行建模估计,通过卡尔曼滤波方程进行滤波处理.

根据式(1)建立的硅微阵列陀螺仪的随机漂移误差模型,第i个陀螺的测量结果可以表示为

yi=ωi+bi+ni

(5)

由于敏感的角速度相同,将任意2个陀螺仪的测量结果进行差分处理可得到随机漂移信息，即

yi-yj=bi-bj+ni-nj

(6)

以b作为状态变量,以陀螺测量结果的差分信号作为量测信号,建立如下硅微阵列陀螺仪的离散Kalman滤波方程:

(7)

式中

Y={y2-y1，y3-y2，y4-y3，y1-y4}T

X={b1，b2，b3，b4}T

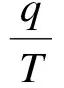
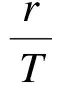
式中，I4为单位矩阵;T为采样周期;q为系统噪声协方差,非负定;r为量测噪声协方差阵,由于量测噪声为角度随机游走白噪声之差,相减仍然为白噪声,其方差阵不变；Vk为观测噪声;X为状态变量;Φ为状态方程;Wk为白噪声序列,均值为零,方差为Qk.

3.3 角速度跟踪模型

动态情况下,陀螺仪敏感角速度的变化可以归结为单目标的角速度跟踪问题.在机动强度不大时,采用Signer模型实现角速度的机动跟踪.Singer模型假定机动加速度a(t)服从一阶时间相关过程,其时间相关函数R(τ)可表示为

(8)

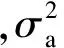
(9)

Xk+1=ΦXk+Wk

(10)

目标观测模型为

Zk=HXk+Vk

(11)

式中,H为观测矩阵，H=[0 1 0];Zk为角速度观测值.

3.4 改进的粒子滤波算法

① 从u～U[0，1]中抽样.

4 实验结果分析

图5为采样频率1 Hz时所得到的随机漂移信号,经动态滤波后的输出如图6所示,实验结果见表2.

图5 硅微阵列陀螺仪的原始漂移

由实验结果可以看出,滤波后硅微阵列陀螺仪的零偏不稳定性减小为51 (°)/h,与滤波前4个陀螺的零偏不稳定性的均值129.6 (°)/h相比,陀螺漂移性能提高了2.54倍,与最好的零偏不稳定性77.5 (°)/h相比,陀螺漂移性能提高了1.52倍.

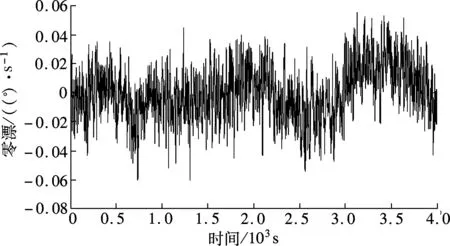
图6 原始漂移的动态滤波器输出

表2 零漂信号的动态滤波实验结果

对于转动角速度分别为50和20 (°)/s的动态滤波实验,实验结果如表3所示.在转动角速度为50 (°)/s的实验中,与滤波前4个陀螺信号的方差均值0.481 0(°)/s相比,原始信号的标准差减小为0.214 9(°)/s，陀螺漂移性能提高了2.24倍.当转动角速度为20 (°)/s时,4个陀螺信号的方差均值为0.473 (°)/s,滤波后信号的标准差减小为原来的41.1%.

表3 匀速转动信号的动态滤波实验结果 (°)/s

5 结语

基于硅微阵列陀螺仪的漂移误差模型,通过对卡尔曼滤波方法和基于角速度动态跟踪的改进粒子滤波方法的数据融合处理，减小了动态信号的噪声,使得硅微阵列陀螺仪的零偏不稳定性提高了2.54倍,验证了模型的有效性.

)

[1] 吉训生,王寿荣. 硅微陀螺阵列信号处理技术研究[J].宇航学报,2009,30(1):235-239.

Ji Xunsheng, Wang Shourong. Research on signal procession of silicon microgyroscope array [J].JournalofAstronautics, 2009,30(1): 235-239. (in Chinese)

[2] Trusov A A,Prikhodko I P,Zotov S A, et al. Low-dissipation silicon tuning fork gyroscopes for rate and whole angle measurements[J].IEEESensorsJournal, 2011,11(11):2763-2770

[3] Walther A, Le Blanc C, Delorme N, et al. Bias contributions in a MEMS tuning fork gyroscope[J].JournalofMicroelectromechanicalSystems, 2013,22(2):303-308.

[4] Zhu Huijie, Jin Zhonghe, Hu Shichang, et al. Constant-frequency oscillation control for vibratory micro-machined gyroscopes [J].SensorsandActuatorsA:Physical, 2013,193(1):193-200.

[5] Bhatt D, Aggarwa P, Bhattacharya P, et al. An enhanced MEMS error modeling approach based on Nu-support vector regression[J].Sensors, 2012,12(7): 9448-9466.

[6] Wang Wei, Lü Xiaoyong, Sun Feng. Design of a novel MEMS gyroscope array[J].Sensors,2013,13(2):1651-1663.

[7] Jiang Chengyu, Xue Liang, Chang Honglong, et al. Signal processing of mems gyroscope arrays to improve accuracy using a 1st order markov for rate signal modeling[J].Sensors,2012,12(2):1720-1737.

[8] 张鹏,常洪龙,苑伟政,等. 虚拟陀螺技术研究[J]. 传感技术学报,2006,19(5):2226-2229.

Zhang Peng, Chang Honglong, Yuan Weizheng, et al. On improving the accuracy of the micromachined gyroscopes based on multi-sensor fusion[J].ChineseJournalofSensorsandActuators, 2006,19(5):2226-2229. (in Chinese)

[9] El-Sheimy N, Hou H Y, Niu X J. Analysis and modeling of inertial sensors using allan variance[J].IEEETransactionsonInstrumentationandMeasurement, 2008,57(1):140-149.

[10] Chib S, Nardari F, Shephard N. Markov chain Monte Carlo methods for stochastic volatility models[J].JouralofEconometrics, 2002,108(1): 281-316.