具有优先权温贮备系统的维修更换模型

程 诚，郑海鹰

（温州大学数学与信息科学学院，浙江温州 325035）

具有优先权温贮备系统的维修更换模型

程 诚，郑海鹰†

（温州大学数学与信息科学学院，浙江温州 325035）

研究了两个不同型部件和一个修理工组成的温贮备可修系统.假定两部件故障之后均不能“修复如新”且部件1具有优先使用权，部件2温贮备故障之后可以“修复如新”.利用几何过程、更新报酬理论，以部件1的维修次数为更换策略，给出了系统经过长期运行单位时间内的平均损失的具体表

温贮备系统；几何过程；优先权；期望损失

可修系统的维修更换策略一直是可靠性理论研究中的一个热点.最初人们关注的是“完美维修模型”，即故障部件或系统经过维修之后可以“修复如新”，在此基础上，人们做了大量的研究工作并取得了很多成果.然而，实际情况并非如此，大多数的可修系统经过维修之后并不能“修复如新”.1983年，Brown等[1]首次提出一种“不完全维修”模型，假定系统经过维修后，“修复如新”的概率为p，最小维修的概率为1-p.随着研究工作的进一步深入，许多学者开始发现，随着部件维修次数的增加，系统的性能会越来越差，同时，故障部件的维修时间也会越来越长，最终会导致系统不能再工作也不能再修理.1988年，Lam[2]首次提出用“几何过程”来描述可修系统的这种随机退化现象.文献[3-6]利用“几何过程”研究了部件在“修复非新”条件下，系统的维修更换问题.以上各种维修模型中大部分都是针对单部件可修系统或冷贮备可修系统的，很少涉及可靠性中另一类可修系统——温贮备可修系统.本文对由两个不同型部件和一个修理工组成的温贮备可修系统进行研究，假定部件工作故障均不能“修复如新”，但部件2在温贮备期间发生故障可以“修复如新”且部件1具有优先使用权，以部件1的维修次数为更换策略，利用“几何过程”理论，给出了系统经过长期运行单位时间内期望损失的具体表达式，最后，通过具体实例验证了最优维修策略的存在性.

1 模型假设及相关定义

1.1 相关定义进行仿真模拟，计算结果见表1及图1.

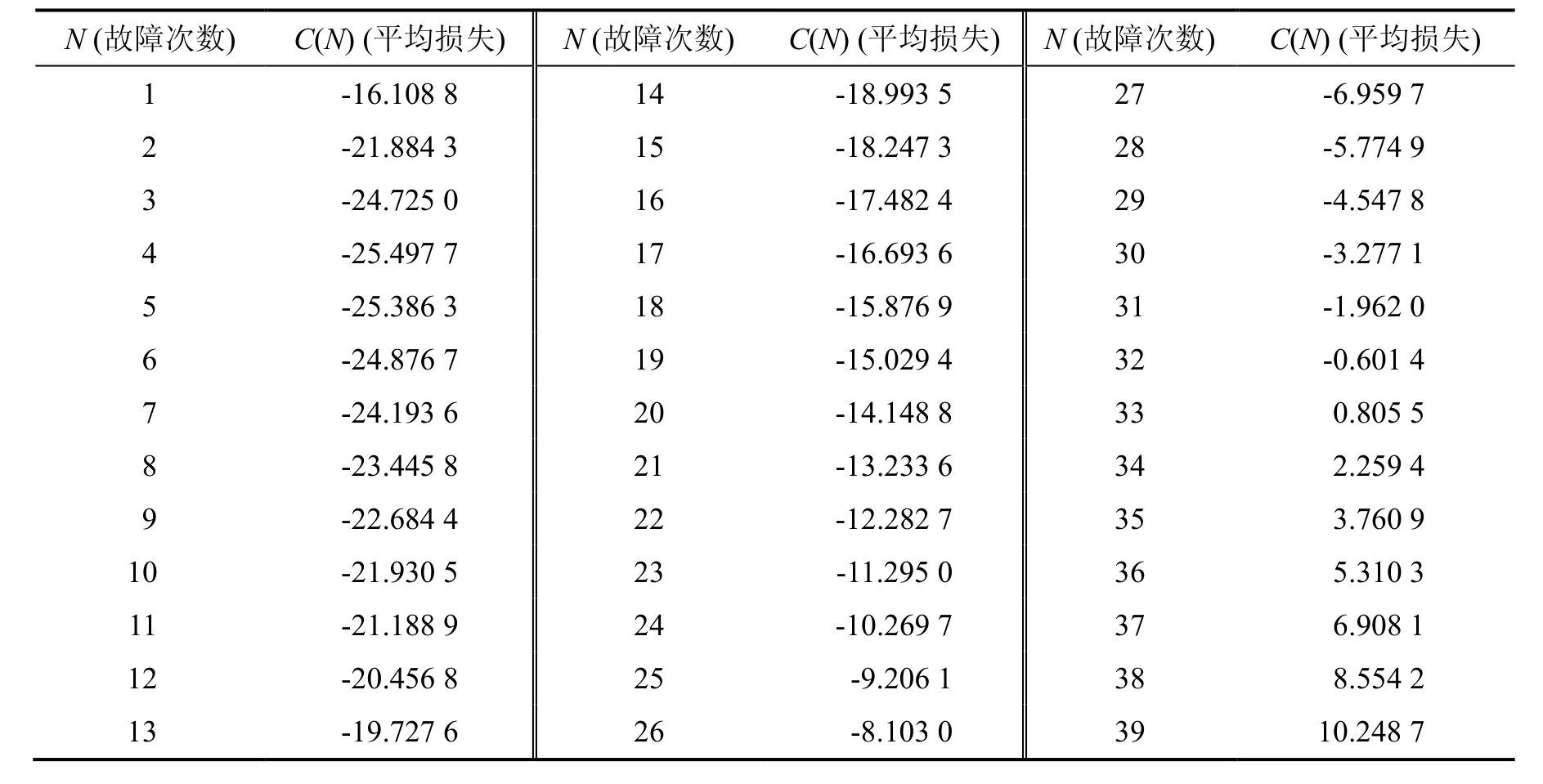
表1 系统的平均损失C（N）随故障次数N的变化情况

由表1可以得知，当N = 4时，C（N）达到最小值为-25.497 7.换言之，系统的最优更换策略为N = 4.从图1中也可以看到，系统的维修更换策略存在并且是唯一的.

5 小 结

本文研究了由两个不同型部件和一个修理设备组成的温贮备可修系统的维修更换策略.在假定部件1具有优先权的情形下，以系统经过长期运行单位时间内的期望损失为目标函数，利用几何过程理论，给出了目标函数的具体表达式，最后，利用Matlab软件进行了数值模拟，得到了系统的最优更换策略.本文的研究方法对于企业的设备维修和更换具有一定的指导意义和参考价值.

图1 系统的平均损失C（N）随故障次数N的变化曲线

[1] Brown M.Imperfect repair [J].Journal of Application Probability, 1983, 20（4）：851-859.

[2] Lam Y.A note on the optimal replacement problem [J].Advances in Applied Probability, 1988, 20（2）：479-482.

[3] Zhang Y L, Wang G J.A deteriorating cold standby repairable system with priority in use [J].European Journal of Operational Research, 2007, 183（1）：278-295.

[4] Zhang Y L.An Optimal Replacement Policy for a Three-State Repairable System with a Monotone process Model [J].IEEE Transactions on Reliability, 2004, 53（4）：452-457.

[5] Wang G J, Zhang Y L.A bivariate mixed policy for a simple repairable system based on preventive repair and failure repair [J].Applied Mathematical Modelling, 2009, 33（8）：3354-3359.

[6] Jia J S, Wu S M.Optimizing replacement policy for a cold-standby system with waiting repair time [J].Applied Mathematics and Computation, 2009, 214（1）：133-141.

Maintenance Replacement Model for Warm-standby System with Priority

CHENG Cheng, ZHENG Haiying
（College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035）

In this paper, a warm-standby system consisting of two dissimilar components and one repairman is studied.Assuming that the two components can not be repaired “as good as new” after fault and component 1 has priority in use while component 2 can be repaired “as good as new” after warm-standby failures.According to the geometric process and renewal reward theory, the specific expression of the average loss within a unit time is given after a long-time running.Finally, the result is to be simulated through some numerical examples, verifying the existence of the optimal replacement policy.

Warm-standby System；Geometric Process；Priority；Expected Loss

O213

A

1674-3563（2013）02-0011-07

10.3875/j.issn.1674-3563.2013.02.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-07-13

程诚（1987- ），男，安徽合肥人，硕士研究生，研究方向：应用统计.† 通讯作者，wzzhying@163.com

达式.最后，通过数值实例对所得结果进行仿真模拟，验证了最优更换策略的存在性.