两种近似计算Caputo导数的有限差分方法

唐致娣，赵廷刚,2

（1.兰州交通大学数理与软件工程学院，甘肃兰州 730070；2.兰州城市学院，甘肃兰州 730070）

两种近似计算Caputo导数的有限差分方法

唐致娣1，赵廷刚1,2

（1.兰州交通大学数理与软件工程学院，甘肃兰州 730070；2.兰州城市学院，甘肃兰州 730070）

有限差分法作为数值求解微分方程的一种手段，已经得到了广泛应用.为了使Caputo导数的计算更加精确，通过有限差分法建立了线性插值（格式I）和分片二次插值（格式II）两种近似的计算格式，并对这两种格式的误差进行了分析和对比，结果表明，格式II可得到更优的误差估计，因此格式II可推广应用到分数阶微分方程的求解中.

Caputo导数；线性插值；分片二次插值

许多物理现象或过程的规律都可以用偏微分方程来描述.有限差分法作为数值求解微分方程的一种手段，已经得到了广泛应用[1-5].在偏微分方程中，对分数阶导数的研究近几年出现得较多.目前，Caputo导数的近似计算普遍使用线性插值进行逼近[6-10]，这种格式的精确度比较好.本文通过有限差分法建立了线性插值和分片二次插值两种近似计算Caputo导数的格式，其中，线性插值格式（格式I）是目前普遍使用的逼近格式，二次分片插值格式（格式II）是本文利用二次分片插值得到的结果，并对两种格式的误差进行了分析和对比，发现格式II得到的精度更高，因此利用格式II能够更精确地求解分数阶微分方程.

1 格式的推导

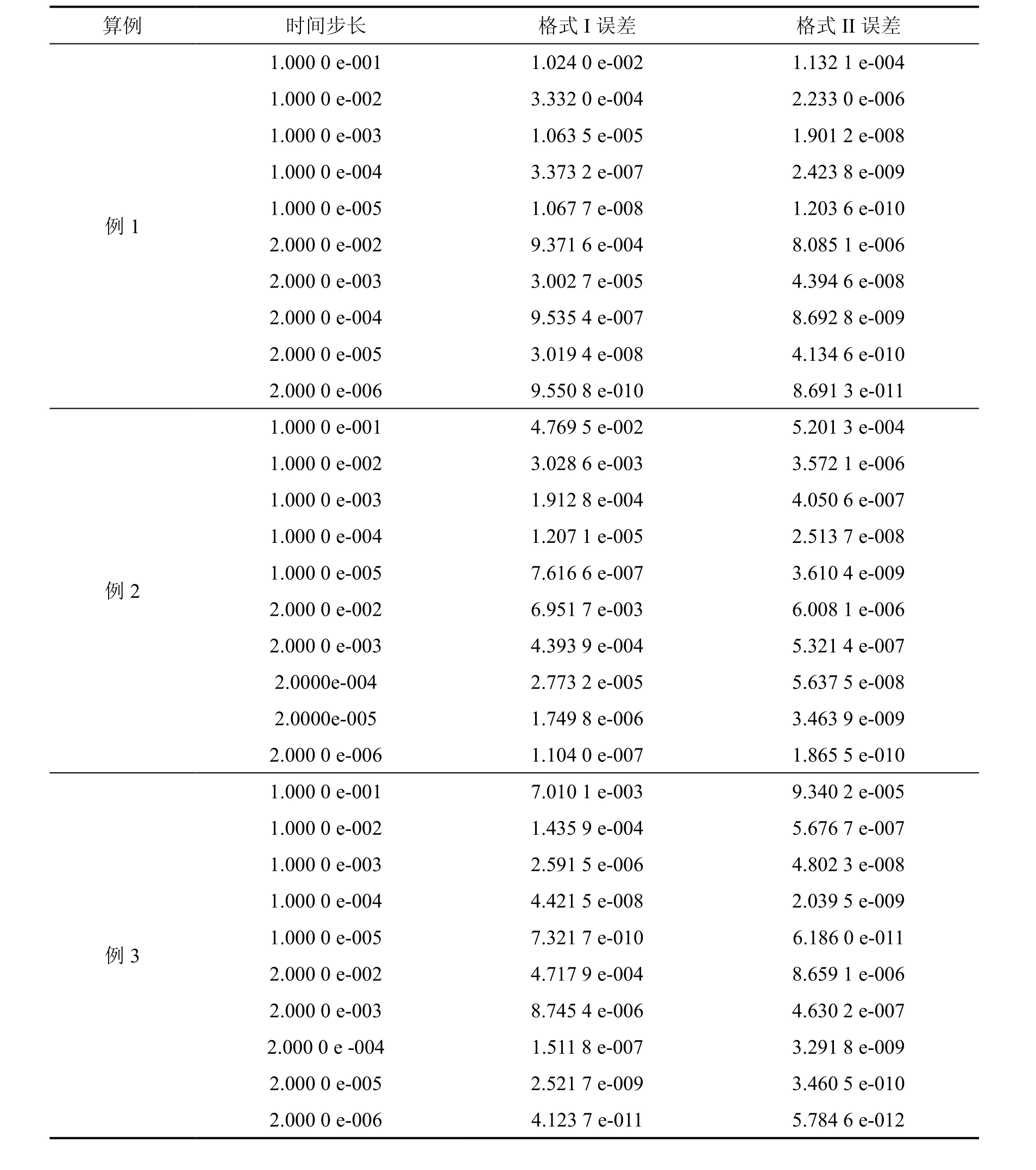
表1 误差分析

[1] Shen B, Shih A J, Xiao G X.A heat transfer model based on finite difference method for grinding [J].Journal of Manufacturing Science and Engineering, 2011, 133（3）：031001.

[2] Chakraborty R, Ghosh A.Finite difference method for computation of 1D pollutant migration through saturated homogeneous soil media [J].International Journal of Geomechanics, 2011, 11（1）：12-22.

[3] Varanasi C, Murthy J Y, Mathur S.A meshless finite difference method for conjugate heat conduction problems [J].Journal of Heat Transfer, 2010, 132（8）：081303.

[4] Kendrick B K.An iterative finite difference method for solving the quantum hydrodynamic equations of motion [J].Journal of Molecular Structure：Theochem, 2010, 943（1-3）：158-167.

[5] Koohkan M R, Attarnejad R, Nasseri M.Time domain analysis of dam-reservoir interaction：using coupled differential quadrature and finite difference methods [J].Engineering Computations, 2010, 27（2）：280-294.

[6] Baleanu D.Fractional constrained systems and Caputo derivatives [J].Journal of Computational and Nonlinear Dynamics, 2008, 3（2）：021102.

[7] Daftardar-Gejji V, Jafari H.Analysis of a system of nonautonomous fractional differential equations involving Caputo derivatives [J].Joumal of Mathematcal Analysis and Applications, 2007,328（2）：1026-1033.

[8] Agrawal O P.Generalized Euler-Lagrange equations and mransversality conditions for FVPs in terms of the Caputo derivative [J].Journal of vibration and control, 2003, 13（9-10）：1217-1237.

[9] Voroshilov A A, Kilbas A A.Existence conditions for a classical solution of the cauchy problem for the diffusionwave equation with a partial Caputo derivative [J].Doklady Mathematics, 2007, 75（3）：407-410.

[10] Diethelm K.The analysis fractional differential equations [J].Journal of Mathematical Analysis and Applications, 2002, 265（2）：229-248.

（编辑：王一芳）

Two Finite Difference Methods for Calculating Caputo Derivative Approximately

TANG Zhidi1, ZHAO Tinggang1,2
（1.School of Mathematics and Software Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070；2.Lanzhou City University, Lanzhou, China 730070）

As a means of numerical solution of differential equations, the finite difference method has been widely used.In order to make the calculation of Caputo derivative more accurate, the paper constructs two approximate calculation formats of linear interpolation （Format I）and slice two interpolation （Format II）through the finite difference method, and makes analyses and comparisons of errors of the two formats.The results show that Format II can obtain a better error estimation, so Format II can be generalized to the solution of fractional differential equations.

Caputo Derivative；Linear Interpolation；Slice Two Interpolation

O241.81

A

1674-3563（2013）02-0001-06

10.3875/j.issn.1674-3563.2013.02.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2012-05-03

国家自然科学基金（11161026）

唐致娣（1986- ），女，甘肃兰州人，硕士研究生，研究方向：运筹学与控制论