量子化学计算方法与GPU应用综述

朱砚

（贵州大学化学与化工学院，贵州贵阳550025）

从化学学科的诞生到量子化学正式出现之间的漫长岁月里，化学一直是作为一门实验科学存在的。从实验中获得经验、总结规律并对各种假说进行验证，是化学学科长久以来发展的方式。但是，量子化学的出现使得数学和化学真正地结合起来，就如1998年诺贝尔化学奖颁奖公告中所说的，“实验与理论能携手协力揭示分子体系的性质。化学不再是一门纯实验科学了”。

量子化学脱胎于量子力学，是量子化学计算的理论基础。1925年海森堡创立了量子力学的形式，1926年薛定谔提出了著名的波动方程（薛定谔方程），1927年海特勒和伦敦应用量子力学原理研究氢分子分子键的原理，标志着量子化学的诞生。

经过多年的发展，随着量子化学理论的进一步深入和计算工具的进步，尤其是在计算设备高速更新、研究手段日新月异的今天，量子化学已成为整个化学学科中不可或缺的一部分。它已经不仅仅局限于传统的分子内和分子间的数值计算，而是渗透到很多相关学科之中，结合生物体系理论模拟和激发态光化学、固体表面与纳米结构体系、复杂体系分子量子动力学和核磁共振理论研究等，在生物大分子、新型催化剂、材料与能源等领域发挥着与实验并重的重要作用[1]。

1 量子化学计算的常见方法

1.1 从头算方法

从头算方法（Ab initio Methods）是仅使用一些最基本的物理常数（如光速、普朗克常数等）作为已知参数，完全利用数学工具来求解薛定锷方程，而不引入任何经验性质的化学参数的一种量子化学计算方法。由于绝大多数化学体系中的薛定谔方程没有严格的解析解，为解决这一问题，1928年提出的Hartree假设，将原子其他电子对第i个电子的排斥作用看成是球对称的、只于径向有关的力场，试图解决多电子体系薛定谔方程近似求解的问题。1930年，Hartree的学生B.A.Fock和J.C.Slater分别提出了考虑泡利原理的自洽场迭代方程和单行列式多电子体系波函数，将Hartree方程推演为Hartree-Fock（HF）方程，满足了多电子波函数的反对称化要求。

对于给定的电子间距，两个反平行自旋的电子不仅仅遵守库仑定理，而且与自旋无关地相互排斥，可通过Hartree-Fock模型解释，并且还受到额外的、依赖自旋的相互作用的影响，被称为“库仑空穴”。对于反平行自旋的电子对，可以认为每个电子被球体屏障包围，两个电子间的距离越短，球体屏障越“坚实”。由于HF方法并没有很好地处理多电子体系中电子之间的相互作用，使得计算结果和实际数值有所偏差，称为电子相关能。HF方法主要未考虑的是库仑空穴的问题，忽略了电子间的排斥作用，而排斥会使得能量升高，使得电子相关能一般为负值。

在Born-Oppenheimer近似、非相对论近似和单电子近似的基础上，把分子轨道用原子轨道的线性组合（LCAO）来表示，薛定谔方程又演变为如下Hartree-Fock-Roothann（HFR）形式：

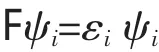
为了使计算结果更加精确，后来又出现了用变分原理处理电子激发态的组态相互作用方法（Configuration Interaction，CI）及衍生出来的CIS，CISD，CISDT，CISD（T），QCISD（T）等方法；多组态自洽场方法（MCSCF）；对Hamilton量作分解和组合的微扰方法；Møller-Plesset微扰理论衍生出的MP2，MP3，MP4等方法；耦合簇理论导出的CCSD和CCSDT等方法。

从头算方法中较原始的HF方法计算速度较快，但精度较低；CCSD（T）、MP4等方法在大幅度提高计算精度的同时，也占用更多的计算资源。因此，从头算方法可以应用在从小体系到大体系，从静态系统到动态系统，从分子内相互作用到分子间相互作用等各个方面，但由于其计算精度和计算速度的矛盾，从头算方法通常更适合于中小体系的定量计算[2]。

1.2 密度泛函理论

密度泛函理论（Density Functional Theory，DFT）最早要追溯到1920年前后，托马斯和费米等人提出的用来描述多电子原子体系的Thomas-Fermi-Dirac近似，与1950年提出的Slater行列式共同成为密度泛函的理论基础。1964年Hohenberg和Kohn的Hohenberg-Kohn模型成为密度泛函理论发展历史上重要的里程碑，证明了多电子体系的非简并和简并基态的能量是单质点（电子）密度的唯一函数，分子基态所有信息都包含在单质点（电子）密度函数中。1965年Kohn和Sham把能量密度函数变分简化为一组单电子薛定谔型方程式，在形式上类似Hartree理论，但对交换能和相关能在局部近似中描述。1975年Srebrenik和Bader证明三维分子空间可分解成量子次空间（quantum subspaces），其边界可由单质点密度性质来规定[3]。由于Kohn在密度泛函理论上取得的伟大成就，与Pople在高斯（Gaussian）量子化学计算程序方面的贡献，两位科学家分享了1998年诺贝尔化学奖。

密度泛函理论在处理电子相关能方面有很大的优势，1998年诺贝尔化学奖颁奖词中对密度泛函理论甚至给出了“量子化学的第二次革命”这样的美誉。与HF方法相比，DFT方法计算速度快，在处理轻元素所形成的基态化合物时候表现相当好，精度甚至能够达到MP2的水平。DFT在频率计算，以及ESR、VCD、NMR方面都有不错的表现，现在已经应用到化学键、分子几何性质、分子间力、化学活性、Xα散射波方法、量子流体动力学等方面的研究。

虽然密度泛函理论的提出极大地推进了计算化学的发展，但是其本身也存在着一些问题。例如：由于纯DFT方法基于单Slater行列式，原则上只适用于基态问题，因此，不适合处理多重态计算和优化。DFT方法中并没有对计算体系提出明确的能量下限，有时候会带来意想不到的麻烦，在处理分子间相互作用的时候尤其需要谨慎对待。以常见的B3LYP为例，（1）计算误差随体系的增大而增长，制约了DFT在较大体系中的应用；（2）不能准确地计算反应能垒，不仅制约了DFT在化学反应动力学中的应用，也使得反应机理的阐明可能出现严重偏差；（3）不能准确地计算非键作用，如严重低估范德华力及P-P堆栈，从而制约了DFT在生物体系中的运用[1]。

1.3 半经验方法

科学家们发现对酶、蛋白质、聚合物等大分子体系进行计算的时候，使用从头算法和密度泛函理论等有严格理论基础的方法，虽然能获得较为精确的结果，但需要占用大量的计算资源，存在计算时间长等缺点。为了在计算时间和计算精度上寻找一个平衡点，人们有意识地忽略了一些计算极其复杂但对结果影响却很小的积分，并引用一些实验数据来近似地求解薛定谔方程，从而提出了半经验的量子化学计算方法，如AM1、PM3、MNDO、CNDO、ZDO，等等。半经验的量子化学计算方法是对严格计算方法的一种补充，可以进行定性或半定量的计算，与严格的计算方法组合使用，可以大量节省计算的时间，并且对精度的影响较小[2]。

2 GPU引发的新一轮量子化学革命

量子化学做为一个理论性很强且计算量很大的化学分支，与计算机技术的发展密切相关，从发表的化学计算论文数量可见一斑。1920年到1950年前后，当时还没有计算机，只有台式的电子计算器，与量子化学计算相关的论文不到60篇。到二十世纪50年代，得益于第一代真空管计算机的出现，十年中全世界有关量子化学的论文迅速增加了10倍，达到600多篇。到上世纪60年代，晶体管第二代计算机的发展，使这十年中的量子化学论文再增10倍，发表的量子化学论文约6000余篇。1970年以来，集成电路的第三代计算机发展，量子化学计算的论文发生了井喷，每年发表的相关论文数量达到惊人的地步。计算机的小型化，使得个人计算机都可以成为不亚于工作站的计算化学的工具，而并行计算技术的广泛应用也使得进行量子化学计算的成本有所降低。有测试表明，在高端PC机LINUX系统下运行Gaussian程序的运算速度完全可以媲美普通的工作站[4]。

最初，量子化学计算速度依赖计算机CPU的性能，从X86系列，到Pentium系列，再到现在的Core系列等，计算机CPU的主频越来越高，计算速度也越来越快。以前计算化学的软件程序是围绕着CPU计算编写的，但是从2007年开始，GPU与量子化学计算的结合引发了量子化学新一轮革命。

GPU（Graphic Processing Units）图形处理器，是计算机中用来处理可视化效果尤其是3D效果的处理器。为了能够使图像更加逼真，每一个GPU中往往包含有上百个计算单元，且可以同时进行并行计算。这样的特性使得GPU成为了比CPU更适合进行科学计算的处理器。早期利用GPU来进行通用并行计算，往往需要将待求解的一般问题转化为图形处理领域的问题，然后才能调用GPU的驱动程序进行计算。随着OpenCL和CUDA等通用并行编程模型的提出，使得基于GPU的并行计算实现已经变得也越来越方便[6]。

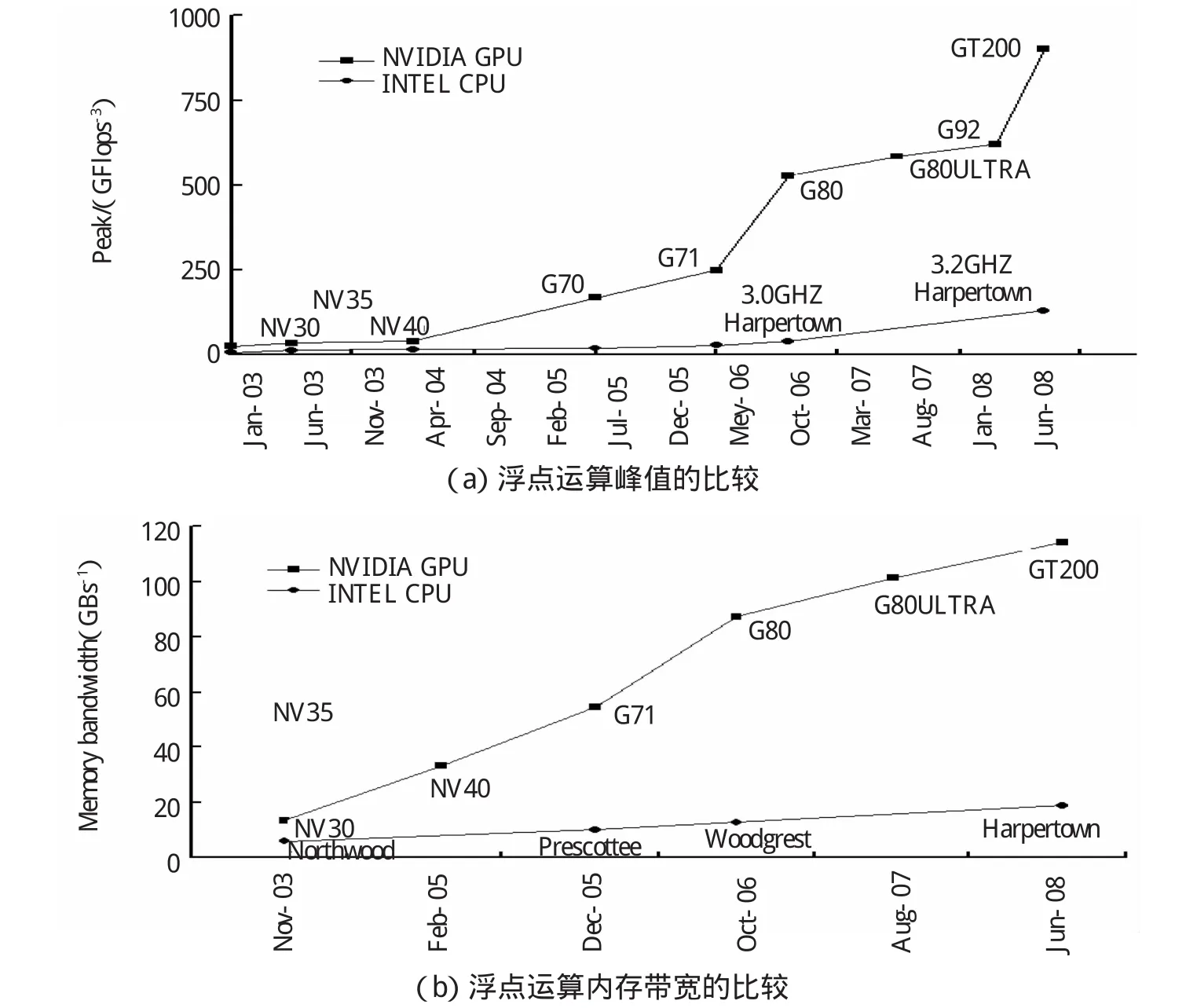
图1 GPU与CPU的浮点运算峰值和内存带宽的比较[7]Fig.1 Comparison of peak speed and memory bandwidth by floating pointoperation between GPU and CPU[7]

从图1中GPU与CPU的浮点运算峰值和内存带宽的比较可以看到，在同等条件下，利用GPU进行化学计算，可以将计算速度提高几倍到几十倍之多。在目前阶段，已经利用GPU已经可以计算s、p、 d轨道的积分，相信在完善了在GPU上计算f轨道及更高的轨道的积分方法以后，凭借GPU的天然优势，GPU计算将会将量子化学计算带入到一个更高的高度[6]。

过去的量子化学计算程序是围绕CPU运算而编写的，改用GPU运算后，需编写能够使用GPU进行运算的程序，是目前需要解决的问题。把原有的算法全部改写成适合在GPU上运行的形式，工作量将十分巨大。目前能够进行GPU运算的量子化学程序包主要有Q-chem、Firefly、GAMESS、BigDFT、TeraChem等，其中大多数都是利用现有的使用CPU进行运算的程序包，改写其中部分算法，在某一特定计算步骤，使计算速度得到提高。而TeraChem是第一个完全基于GPU运算而编制的量子化学计算程序，具有蓬勃发展的潜力。

3 结语

计算化学的兴起代表了化学的复兴，未来的应用领域也将更加广泛，除了当前已有的发展方向和应用领域，还将用明确包含时间依赖和相对论效应来改进现在的波函数，从扩展分子动力学发展到有边界条件的非平衡，展现出一个更加清晰的量子理论，并带领分子动力学走向实实在在的生物模拟和生物细胞模型。随着计算机技术的发展和各种计算方法、计算程序的不断改进，量子化学计算的精度会更高、速度会更快、范围会更广，还将在与生物、材料、能源、医学、天文等多学科的交叉中，发挥其不可替代的作用。

［1］ 苏培峰,谭凯,吴安安,等.理论与计算化学研究进展［J］.厦门大学学报（自然科学版），2011，（2）:311-318.

［2］ 郑文锐.计算化学在化学化工中的应用（上）［J］.上海化工, 2009，（12）:22-24.

［3］Enrico Clementi,Giorgina Corongiu,帅志刚,等.从原子到大分子体系的计算机模拟——计算化学50年［J］.化学进展,2011，（9）: 1795-1830.

［4］ 何禹,王一波.个人计算机和工作站上计算化学软件性能的综合测评［J］.计算机与应用化学,2003,（Z1):175-178.

［5］ 陈智强.自由基聚合反应过程动态分子量分布的并行计算方法研究［D］.浙江大学,2011.

［6］鲍建樟,丰鑫田,于建国.GPU引发的计算化学革命［J］.物理化学学报,2011,（9）:2019-2026.