重塑试样差异性对土-水特征曲线影响试验研究
杨 钢,杨 庆,刘文化
(大连理工大学 土木工程学院 岩土工程研究所,辽宁 大连 116024)
0 引 言
在非饱和土研究中,基质吸力与含水量(如重量含水量、体积含水量或饱和度)之间的关系称为土水特征曲线(SWCC).土水特征曲线是非饱和土研究中必不可少的工具,对于理解非饱和土力学性质,获取模型参数具有重要作用,并在路基工程、废物控制和渗流场数值模拟等工程中[1-3]得到应用.从土水特征曲线字面来看,Nuth等[4]认为其中的“特征”一词,表明土水特征曲线是土的固有属性,即对于某种土而言,土水特征曲线应当是唯一的,但大量试验研究证明土水特征曲线受颗粒级配、矿物成分、孔隙结构、密实程度和土的应力历史、温度等因素的影响[5-8],因此试验结果并不是唯一的.在诸多影响因素研究中,通常将同等条件下制作的试样看作是均一的.然而许多研究发现无论是重塑土样还是原状土样,亦或是膨胀土、黄土等特殊土[9-10],试样自身的差异都将影响土水特征曲线,但这一情况并没有被详细研究,仅通过取平均值的方法来消除其影响.原状土样获取中易受到扰动而难以保证其原始状态,因此重塑土样是本次研究的重点.
对于重塑土样而言,其差异主要是由试样重塑技术局限性引起的.目前重塑技术主要通过控制初始干密度和初始含水量来保证试样孔隙比的一致性,而对具有明显随机性的孔隙尺寸与分布难以控制,这必然会对孔隙连通性产生影响,而孔隙连通性则会对土水特征曲线造成严重影响[11].因此即便是同等条件下制作的试样,它们的土水特征曲线也可能产生差异.李顺群等[12]通过击实试样分段研究发现土水特征曲线沿高度方向发生右移.Simms等[13]发现试样尺寸将对孔隙尺寸分布(PSD)产生明显影响,因而也会造成土水特征曲线的差异.目前土水特征曲线研究往往通过环刀试样进行,这种做法虽然加快了平衡时间,但必然与三轴试样的实际情况不符,本文将对三轴试样进行研究.
1 理论分析
非饱和土研究中,可将孔隙看作不同半径毛细管的集合体,因此本文用双孔隙模型来阐述孔隙尺寸与分布的随机性产生的影响.这里假设模型仅考虑孔隙的竖向随机分布,孔隙水由上部向下排出.两个孔隙半径分别为R1和R2,其中R1>R2,相应的孔隙排水条件分别为ua1与ua2.在土水特征曲线研究中,基质吸力依次施加、逐级增大,因此假设孔隙气压力变化为0→ua1→ua2.基于上述假定,孔隙将出现图1所示的两种随机分布情况.在图1(a)中,当施加孔隙气压力ua1,R1中的孔隙水V1将从陶土板排出,而R2中的孔隙水V2将继续保持,直到孔隙气压力达到R2排水条件ua2;在图1(b)中,当孔隙气压力为ua1时,R1与R2中的孔隙水都将保持不变,表现出“瓶颈”效应,直到孔隙气压力达到ua2,R1与R2中的孔隙水都将排出.因此当ua1<ua<ua2时,图1(a)中的剩余孔隙水体积Va=V2,而图1(b)中的剩余孔隙水体积Vb=V1+V2,两者的含水量明显不同.但当ua>ua2时,两种情况下孔隙中的水都将排出,剩余孔隙水体积为零.从上述分析可以看出试样在某一基质吸力下可能具有明显不同的含水量,但是随着基质吸力增大,含水量的差异可能减小.
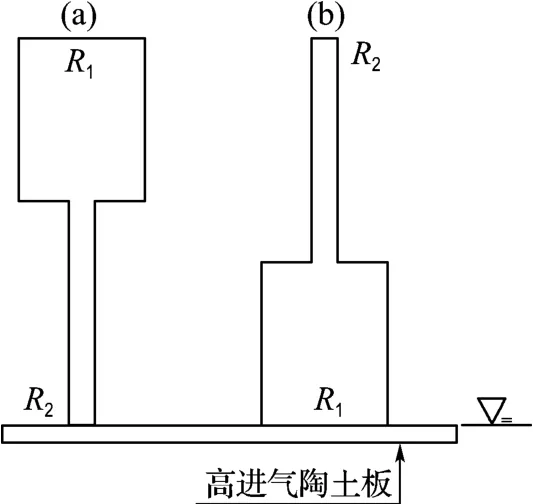
图1 双孔隙结构随机分布示意图Fig.1 The schematic diagram of random distribution for double pores system
2 室内试验
2.1 试样准备
试验用土来自大连地区典型粉质黏土,土料经自然风干碾碎后过1mm 筛备用,其天然含水量为5.32%,塑限为12.5,液限为25.6,塑性指数为13.1.试样直径39.1mm,高80mm;初始含水量为16.1%,初始干密度为1.73g/cm3,初始孔隙比为0.552.制样采用湿捣法,土料分5层装入饱和容器,分层击实,并控制各试样的密度差值小于0.02g/cm3,试样制备好后进行抽真空饱和.为防止平衡过程中试样碰撞、拿取受损,本次试验以亚克力材质制作对开模.对开模内径为39.3mm,外径为50.0mm,高度为80.0mm;对开膜中部刻有凹槽,在包裹试样后,将高弹橡胶圈滑入凹槽内,以保证试样与对开膜稳定.试验前需在对开模表面涂一层凡士林,以保证对开模与试样表面的密闭性,减少柱面气体侵入而引起的排水通道阻隔,以尽量保证孔隙水从上部开始向下排水,避免影响到基质吸力平衡的测量.
2.2 试验方法
试样脱湿平衡采用美国Soilmoisture 公司1250体积压力膜仪,高进气陶土板最大进气值为500kPa.仪器采用轴平移技术控制吸力,通过设定孔隙气压力与水压力保证试样达到预定的吸力,体积压力膜仪孔隙水压力默认为零,因此只需设定孔隙气压力值.体积压力膜仪未配备数据采集系统,试样的含水量变化需通过记录试样质量获取,因此采用Sartorius精密天平称量试样,其称量范围为610g,精度为0.01g.本次试验仅对脱湿平衡中获得的干燥曲线进行研究,其基质吸力试验量测范围为0~350kPa.
饱和试样称量后放入体积压力膜仪中,平衡后取出称量,根据式(1)计算当前试样饱和度.试样放回体积压力膜仪前,用细毛刷蘸水轻刷高进气陶土板表面,在其表面覆盖一层无气水膜,使得试样放回后与高进气陶土板紧密接触,保证孔隙连通性.整个试验过程中,每24h记录一次数据,并规定每级基质吸力至少测量10d.
试样体积含水率
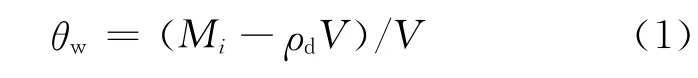
式中:Mi为平衡过程中每次称量试样质量;ρd 为试样干密度;V为试样总体积.
在试验结束后,对4个试样采用烘干法测量其最终含水量,实测值占计算值的95.5%~98.0%.因此整个过程中,对开模很好地保护了试样,保证了试验结果(见表1).

表1 试样最终含水量的计算值与实测值Tab.1 The calculated value and measured value of final water content of sample
3 试验结果与分析
3.1 土水特征曲线试验分析
图2显示了体积含水率-基质吸力表示的4个试样的土水特征曲线,4 个试样依次记为S1、S2、S3和S4.由图中可以看到,体积含水率在每级基质吸力下均存在着差异,特别在100kPa基质吸力处出现明显区分.根据进气值与残余饱和度概念,土的脱湿过程一般可以分为边界效应段、过渡段和非饱和残余段三部分[14].当基质吸力以图3所示的单对数形式表示,可以看出整个试验数据属于过渡阶段,因此在图2中再次将其划分为两个阶段.
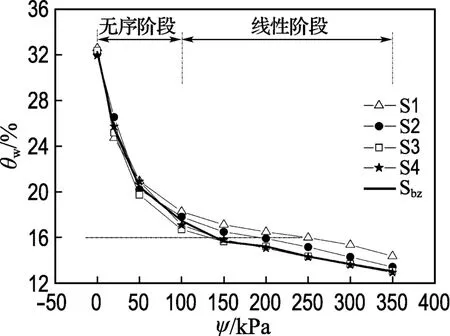
图2 土水特征曲线Fig.2 The soil-water characteristic curve
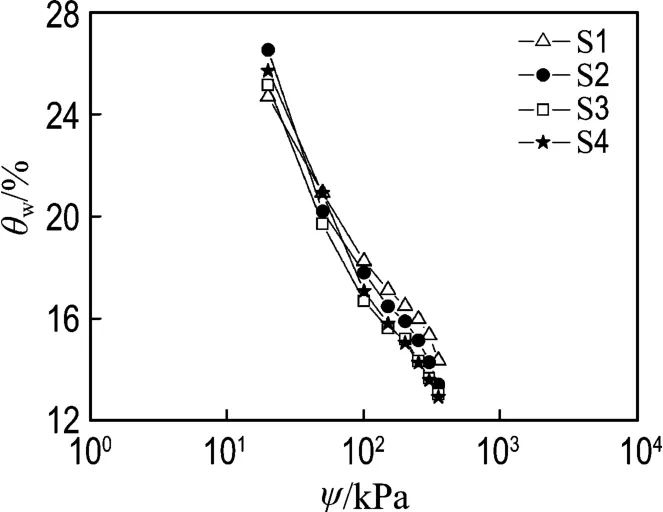
图3 单对数土水特征曲线Fig.3 The single logarithmic soil-water characteristic curve
在无序阶段,试样排水情况极不稳定.若将同一基质吸力下的试样体积含水率从大到小排列,并用1、2、3、4表示(其中1为同一基质吸力下的最大体积含水率,4为同一基质吸力下的最小体积含水率),从图2可以看出:试样S1 在20kPa基质吸力时,为体积含水率最小的试样,即为4,而在50kPa基质吸力下则成为体积含水率最大的试样,即为1;试样S2的体积含水率排列情况则在20、50和100kPa基质吸力下经历了1→3→2的明显变化.显然在这一阶段,试样的体积含水率处于随基质吸力增加而突变的“无序”状态.对比图1所示情况,这种试样间体积含水率的跃迁表明试样内部孔隙分布存在明显差异,并导致“瓶颈”效应等情况产生,因此试样的排水情况极不稳定.
Jotisankasa等[15]认为在高吸力下,土水特征曲线对土体结构的依赖将减小,而更趋于均匀.从图2可知:在4个试样中,试样S2、S3、S4间的体积含水率差异随着基质吸力的增加而明显减小;试样S1的体积含水率在350kPa基质吸力前变化较小,这表明试样S1受孔隙随机分布影响更为明显,导致试样在本试验采用的基质吸力范围内排水困难,但随着基质吸力增大,将如双孔隙模型分析结果所示,排水增加,体积含水率差异将减小;因此本次试验结果符合Jotisankasa等的结论.显然随着基质吸力的增大,孔隙分布随机性对土水特征曲线的影响将减弱.而对比无序阶段与线性阶段的体积含水率变化可知,在线性阶段试样间的体积含水率未发生跃迁,变化稳定,因此孔隙分布未在线性阶段产生新的差异,其最初的差异主要是无序阶段影响的延续.
在脱湿条件下,土水特征曲线的体积含水率与基质吸力应当一一对应.对比上述结果可知,在无序阶段体积含水率对基质吸力极为敏感,一个小的基质吸力变化会引起体积含水率明显变化,而在同一基质吸力下对应的体积含水率却基本一致.因此基质吸力的变化是主导,而试样自身引起的体积含水率差异远小于基质吸力引起的体积含水率变化,因此用平均值来描述这个阶段的土水特征曲线是合理的.
线性阶段的基质吸力对体积含水率的敏感性增强,并在试样间产生类似残余阶段情况,如图2中体积含水率为16%处,试样间的基质吸力差异超过100kPa,因此无序阶段之后的各试样间体积含水率的差异不容忽视.值得注意的是:随着基质吸力增大,试样S4从100kPa基质吸力开始突变至与试样S3 的土水特征曲线保持一致,试样S2的土水特征曲线逐渐向S3接近,同时试样S3的体积含水率基本保持相对最小.这些现象表明试样S3的孔隙结构合理,形成了稳定的排水通道,考虑Jotisankasa等的研究,可以预见随着基质吸力的增大,试样的体积含水率将基于试样S3的试验结果而趋于一致.
从上述结果可以看出,随着基质吸力的增大,各试样的土水特征曲线将以某一试样为基准而趋于一致,因此该试样在不同基质吸力下的孔隙分布多表现出图1(a)的理想情况,孔隙与基质吸力可视为一一对应,从本文的试验结果来看,该试样的平衡含水率应当始终保持最低,考虑到土体的复杂性和变异性,将体积含水率稳定保持为最小或接近最小的试样为线性阶段的基试样.本文中S3即为线性阶段的基试样.
基于上述分析:将整个阶段的土水特征曲线用无序阶段平均值和线性阶段基试样的试验数据来表示,这里定义为表征土水特征曲线(记为Sbz).由于平均法是处理数据的常用方法,本文将对两种方法获得的数据进行对比分析,其中平均数据所得的土水特征曲线记为Savg.
3.2 土水特征曲线拟合
土水特征曲线需转化为数学模型,才能应用于渗流、本构方程等相关计算中.目前常用的数学模型包括Brooks &Corey模型、Van Genuchten模型和Fredlund & Xing模型.Brooks &Corey模型虽然简单,模型中参数的物理意义也明确,但拟合效果较差,本文未作考虑.Van Genuchten和Fredlund &Xing四参数模型较为复杂,但拟合效果最好,为此本文对这两个模型的拟合效果进行比较.
Van Genuchten模型:

Fredlund &Xing模型:
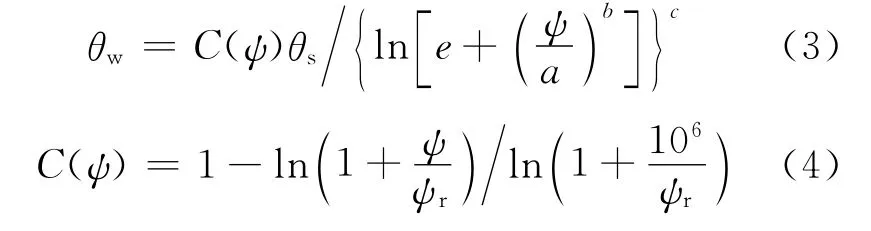
式中:θw为体积含水率;θs为 饱和体积含水率;θr为残余体积含水率;ψ为基质吸力;ψr 为残余体积含水率对应的基质吸力;a、b、c为材料参数.
Van Genuchten模型和Fredlund &Xing模型拟合结果分别见表2和表3.

表2 Van Genuchten模型拟合结果Tab.2 The fitting result of Van Genuchten model
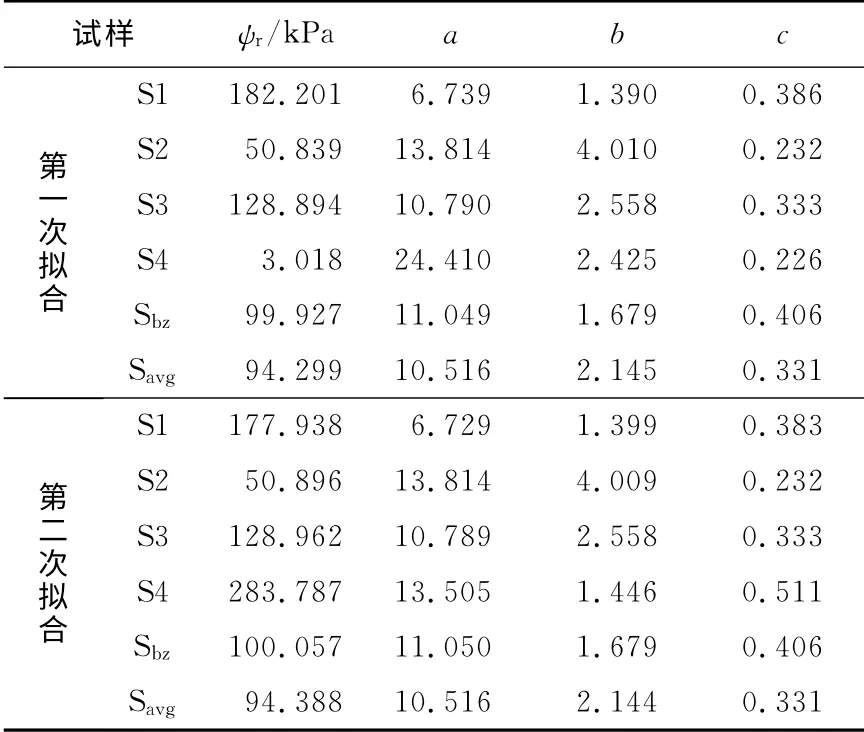
表3 Fredlund &Xing模型拟合结果Tab.3 The fitting result of Fredlund &Xing model
从拟合结果看,表3中试样S4的参数ψr 的第一次拟合结果存在异常,远小于参数a,而参数a一般认为与进气值相关,显然这个结果并不合理.通过试验数据的影响分析发现,0kPa基质吸力的试验数据对拟合结果完全没有影响,而从表2和表3的第一次拟合结果来看进气值应当大于0.1kPa,因此0.1kPa基质吸力与饱和含水率可组合为一组有效试验数据,进而得到第二次拟合结果.对比两次结果可以看出:除S4在Fredlund&Xing模型中拟合值,其他拟合结果基本一致,这表明假定0.1kPa为有效数据是合理的;对比S4的两次拟合值,显然ψr 第二次拟合结果更为合理,因此采用第二次拟合数据绘制相应的拟合曲线图4和图5.
从图4可以看出,Van Genuchten模型拟合的土水特征曲线仅在试验数据范围内基本符合;当大于350kPa基质吸力后,随着基质吸力的增大,各试样差异越来越明显.而图5所示的Fredlund &Xing模型拟合曲线,不仅在试验数据范围内符合较好,并且随着基质吸力的增大呈现趋于一致的趋势(这种结果应当与公式引入修正系数C(ψ)有直接关系),因此Fredlund &Xing模型的拟合结果更符合本次研究的试验数据和相关结论.
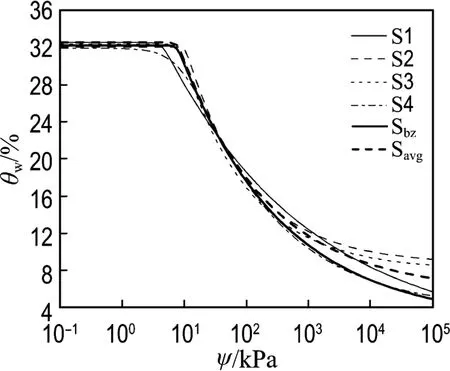
图4 Van Genuchten模型拟合土水特征曲线Fig.4 The fitting soil-water characteristic curve with Van Genuchten model

图5 Fredlund &Xing模型拟合土水特征曲线Fig.5 The fitting soil-water characteristic curve with Fredlund &Xing model
对比两种模型拟合得到的曲线Sbz和Savg可以发现:在试验的基质吸力范围内Sbz和Savg都表现出较好的一致性,但随着基质吸力增大Van Genuchten 模 型 中Sbz和Savg的 差 异 明 显,而 在Fredlund &Xing模型中这种差异扩大的现象也存在.值得注意的是:两种模型中Sbz的拟合结果始终保持了较好的稳定性,在超出试验数据部分的拟合结果始终保持了最低的体积含水率,并呈现出随基质吸力增大而不断降低的趋势,特别在Van Genuchten模型中,并没有因采用S3的试验数据而产生大的变化,并且拟合结果符合试验分析与Jotisankasa等[15]的研究结果;Savg作为平均值,受到多个试样结果的影响,在两种模型中出现明显的差异,数据稳定性差.因此在已有试验数据的基础上,以基试样为基础的试验数据可以合理地表达大于试验基质吸力后土水特征曲线的发展规律,相对于平均法更具优势.
3.3 脱湿试验时程曲线分析
土水特征曲线是非饱和土研究的基础性环节,但其试验往往耗费数月的时间,这也正体现了非饱和土研究的耗时性.通过每日体积含水率与排水量m变化的研究,进一步分析脱湿试验中的现象,并对非饱和土试验研究提出一些建议,以改进非饱和土试验.
图6显示了每日体积含水率的变化情况.从图中可以看出:在20kPa基质吸力下,试样的体积含水率出现差异,但这种差异并不是一开始就存在的,而是随着时间的增加逐步增大的,特别在试验最初的几天,各试样的体积含水率基本一致,这是由于此时的排水主要在大孔隙中产生,因此在孔隙气体侵入试样初期,排水情况一致;但随着时间的增加,试样的体积含水率逐渐降低,排水过程中遇到的孔隙情况愈加复杂,孔隙的随机性也将引起排水路径的变异,进而导致各试样不同的排水情况,造成试样间体积含水率的明显差异.在无序阶段,试样间差异基本保持了这一变化比例,这表明起始基质吸力(即首次施加的基质吸力)对整个土水特征曲线的发展有重要影响.

图6 每日体积含水率时程曲线Fig.6 The curve of volumetric water content versus time
图7显示了每日试样的排水量.从图中可以看出,在100kPa 基质吸力后(脱湿平衡50d后),排水量锐减,其相应的平衡时间也明显减少,但排水情况保持稳定,这表明土体内稳定的排水通道逐渐形成.试样平衡的排出水量主要在最初2~3d内完成,因此测量记录最好在2~3d后开始,以减小重复测量对试样平衡的影响.

图7 每日排水量时程曲线Fig.7 The curve of water discharge versus time
4 结 论
(1)试样差异性影响下的土水特征曲线可以用无序阶段平均值和线性阶段基试样的试验数据相结合表征的土水特征曲线来描述.
(2)对于本次研究而言采用Fredlund &Xing模型更为合理,这应当与公式引入修正系数C(ψ)有直接关系.从拟合过程来看,可以通过合理的假定来增加有效数据,以获得更为合理的拟合结果.
(3)体积含水率随时间的变化表明起始基质吸力对试样间差异的产生有重要影响,应当针对试验情况进行合理选择.排水量随时间的变化表明试样平衡的排出水量主要在最初2~3d完成,因此在主排水结束之后开始测量可以降低相关操作引起的土水特征曲线误差.
[1] Oberg A L.Negative pore pressures-seasonal variation and importance in slope stability analysis[C]// Proceedings of the First International Conference on Unsaturated Soils.Rotterdam:Balkema A A,1995:907-913.
[2] Blatz J,Graham J.A system for controlled suction in triaxial tests[J].Geotechnique,2000,50(4):465-469.
[3] Patil N G,Rajput G S.Evaluation of water retention functions and computer program“Rosetta”in predicting soil water characteristics of seasonally impounded shrink-swell soils [J].Journal of Irrigation and Drainage Engineering,2009,135(3):286-294.
[4] Nuth M,Laloui L.Advances in modelling hysteretic water retention curve in deformable soils[J].Computers and Geotechnics,2008,35(6):835-844.
[5] Miller C J,Yesiller N,Yaldo K,etal.Impact of soil type and compaction conditions on soil water characteristic [J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2002,128(9):733-742.
[6] 龚壁卫,吴宏伟,王 斌.应力状态对膨胀土SWCC的影响研究[J].岩土力学,2004,25(12):1915-1918.GONG Bi-wei,WU Hong-wei,WANG Bin.Influence of stress states on soil-water characteristics of expansive soils[J].Rock and Soil Mechanics,2004,25(12):1915-1918.(in Chinese)
[7] 汪东林,栾茂田,杨 庆.重塑非饱和黏土的土-水特征曲线及其影响因素研究[J].岩土力学,2009,30(3):751-756.WANG Dong-lin,LUAN Mao-tian,YANG Qing.Experimental study of soil-water characteristic curve of remolded unsaturated clay [J].Rock and Soil Mechanics,2009,30(3):751-756.(in Chinese)
[8] 张雪东,赵成刚,蔡国庆,等.土体密实状态对土-水特征曲线影响规律研究[J].岩土力学,2010,31(5):1463-1468.ZHANG Xue-dong,ZHAO Cheng-gang,CAI Guoqing,etal.Research on influence of soil density on soil-water characteristic curve[J].Rock and Soil Mechanics,2010,31(5):1463-1468.(in Chinese)
[9] 刘晓敏,赵慧丽,王连俊.非饱和粉质粘土的土水特性试验研究[J].地下空间,2001,21(5):375-378.LIU Xiao-min,ZHAO Hui-li,WANG Lian-jun.Experimental study on soil-water character of unsaturated powder clay[J].Underground Space,2001,21(5):375-378.(in Chinese)
[10] 陈 伟,孔令伟,郭爱国,等.吸力对弱膨胀土强度贡献的试验研究与预测分析[J].岩土力学,2008,29(7):1783-1787.CHEN Wei,KONG Ling-wei,GUO Ai-guo,etal.Experimental study and predictive analysis of contribution of matrix suction to shear strength of weak expansive soil[J].Rock and Soil Mechanics,2008,29(7):1783-1787.(in Chinese)
[11] Berkowitz B,Ewing R P.Percolation theory and network modeling application in soil physics[J].Surveys in Geophysics,1998,19(1):23-72.
[12] 李顺群,高凌霞,任庆新.三轴击实试样的土-水特征曲线分布[J].武汉理工大学学报,2007,29(6):89-92.LI Shun-qun,GAO Ling-xia,REN Qing-xin.Distribution of soil-water characteristic curves of impacted silty clay triaxial samples[J].Journal of Wuhan University of Technology,2007,29(6):89-92.(in Chinese)
[13] Simms P H,Yanful E K.Measurement and estimation of pore shrinkage and pore distribution in a clayey till during soil-water characteristic curve tests [J].Canadian Geotechnic Journal,2001,38(4):741-754.
[14] 张雪东.土水特征曲线及其在非饱和土力学中应用的基本问题研究[D].北京:北京交通大学,2010.ZHANG Xue-dong.Research on the principle problem relating to soil-water characteristic curve and its application in unsaturated soil mechanics[D].Beijing:Beijing Jiaotong University,2010.(in Chinese)
[15] Jotisankasa A,Vathananukij H,Coop M R.Soilwater retention curves of some silty soils and their relations to fabrics [C]// Unsaturated Soils:Theoretical and Numerical Advances in Unsaturated Soil Mechanics -Proceedings of the 4th Asia Pacific Conference on Unsaturated Soils.Newcastle:CRC Press,2010:263-268.

