重力坝-库水-地基相互作用分析方法比较研究
王铭明,陈健云,徐 强
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.昆明理工大学 电力工程学院,云南 昆明 650500)
0 引 言
强烈地震会给大坝与库水区带来严重的后果,所以研究并掌握坝-库系统的动力反应极为重要.自从1933年Westergaard提出刚性直立坝面的动水压力公式[1]以来,许多学者相继提出了很多坝-库系统的计算模型,丰富了这方面内容,同时也取得了丰硕的研究成果.除了简单的附加质量模型外,1973年Chakrabarti和Chopra[2-4]相继对附加质量模型做出修正,考虑了可压缩性水和弹性坝体的相互作用;而后,Chopra与其合作者作了进一步的研究[5-7],将坝体与地基的相互作用考虑到坝体动力分析中;近年来,Darbre[8]改进了附加质量模型,对附加质量附以黏滞阻尼并通过两个参数限制附加质量的放大作用;最近,Dominguez等[9-11]用边界元模型计算了坝体地震响应的三维效应,取得了很大成果.
考虑到坝体与库水相互作用的耦合关系,很多学者通过各种方法建立耦合模型.最初,Brathez等假设坝体变形为一条直线,应用迭代法计入坝体变形对动水压力的影响[12];随着有限元法的出现,许多学者基于有限元法建立了很多流固耦合模型[13].坝体-库水相互作用的流固耦合模型将坝体和库水看作两个子结构,分别采用不同的单元建模,然后应用有限元法耦合求解.这样可以考虑库水可压缩性、坝体阻尼以及水动力波等效应.Du等[14-15]提出一种时域显式分析方法,严格模拟了可压缩水-拱坝-地基相互作用,计算了小湾拱坝-库水相互作用,取得良好效果;林皋等[16-17]应用比例边界有限元法计算坝体-库水相互作用,具有精度高、维数低、计算速度快的特点.
基于Westergaard公式计算动水压力及其附加质量模型模拟地震时上游库水对坝体的影响,由于简单、方便以及在一定程度上能够反映实际工程的近似情况,从而得到工程界与学术界有条件的承认,但对其适用条件仍有很大争议.本文考虑水的可压缩性,采用拉格朗日法[18]进行5种高度的坝体-库水相互作用的有限元分析,求得坝体的地震动力响应;通过分析给出Westergaard公式及附加质量模型适用的坝体高度范围,验证在计算高坝-库水相互作用时流固耦合模型是否更接近真实情况;同时,还分别研究柔性地基对高低坝体及其库水系统的不同影响.
1 动水压力数值模型
1.1 Westergaard公式及附加质量模型
Westergaard研究了垂直刚性挡水坝在水平简谐振动下的动水压力问题,给出了近似的动水压力计算公式:
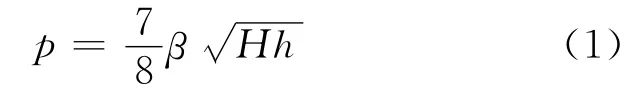
式中:p为动水压力;H为水库的深度;h为计算点水深;β为最大地震加速度系数.
根据坝面动水压力与惯性力的性质相似,与加速度大小成正比、方向相反,所以可以用附着于坝面的一定质量的水体代替动水压力的作用,而导出了著名的附加质量公式:

式中:m(h)为h水深点的附加质量;ρ为水的密度.
采用有限元法计算动水压力时,需在坝体上游面添加附加质量单元模拟库水作用,其中坝体为柔性体,因此在地震动作用下坝体峰值加速度(PGA)会随着坝体高度的增加有所放大.这使得附加质量模型算得的上游面动水压力除坝踵外均在Westergaard公式解基础上有所放大.
1.2 拉格朗日库水有限元流固耦合模型
假设库水为无旋无黏、可压缩水体,其运动方程可表示为

考虑库底吸收性,水库底部边界条件应该为

式中:α是反射系数,0≤α≤1,α=1表示全反射,α=0表示全吸收;n为库底边界法向,c为水体波速.
在设定库水自由面、坝体上游面、上游无限远及库底边界之后,库水流体经2D 有限元离散,某点的动水压力可表示为

对式(3)微分,根据Galerkin法离散后得到流体运动方程:

2 计算实例与结果分析
2.1 计算实例
上部坝头尺寸以阿海重力坝16#挡水坝段为例,保持下游面坡比为0.75不变,取70、100、130、160及200m 五个高度等级重力坝分别进行了流固耦合模型与附加质量模型的地震动力响应计算结果的对比分析.计算时,采用水平和竖直的双轴规范人工谱地震波,水平向地震峰值加速度为0.2g,竖直向地震峰值加速度为水平向的2/3;坝体模型材料的弹性模量为20 GPa,密度为2 400kg/m3,泊松比为0.17;库水模型材料的体积模量为2.3GPa,密度为1 000kg/m3;库水域长度为3倍坝高;动力增强因子取值1.3.
2.2 计算结果分析
2.2.1 频率分析 5种坝体空库及满库时的基频见表1.可以看出,随着坝体高度的增加,满库较空库坝体基频降低的幅度明显增加,从70m 坝高的12.53%,到200m 坝高的20.40%,表明动力作用下库水对高坝的影响较低坝更加明显;对比表1中附加质量模型与流固耦合模型满库坝体频率结果还可知,随着坝高的增加,附加质量模型模拟库水对坝体的作用较流固耦合模型明显偏大.
表2列出70~200m 坝体的高阶振型中最大参与系数及其对应于规范反应谱(Ⅰ类场地)的放大系数.显而易见,高阶振型最大参与系数随着坝高的增加而增大,当坝体高度超过160 m 时,高阶振型最大参与系数超过0.5,坝高超过180 m时,该系数超过0.6,可见高坝动力计算时不可忽略高阶振型影响.从低坝到高坝的各高阶振型中,最大参与系数所在振型是不同的;70~80m 坝体的第6阶振型的参与系数最大,90~110 m 坝体的第5阶振型的参与系数最大,120~150m 坝体的第4阶振型的参与系数最大,160~200m 坝体的第3阶振型的参与系数最大.从表2可知,重力坝随着坝体高度的增加,频率降低,一方面高坝高阶振型动力反应参与系数也会增大,另一方面最大参与高阶振型对应于规范反应谱(Ⅰ类场地)的放大系数会变大.图1给出70、100、160及200m坝体的一阶振型及具有最大参与系数的高阶振型图.从高阶振型图可以看出坝体的头部反应较大,而且坝体越高反应越强烈.

表1 不同工况下坝段的基频Tab.1 Dams fundamental frequencies under different cases
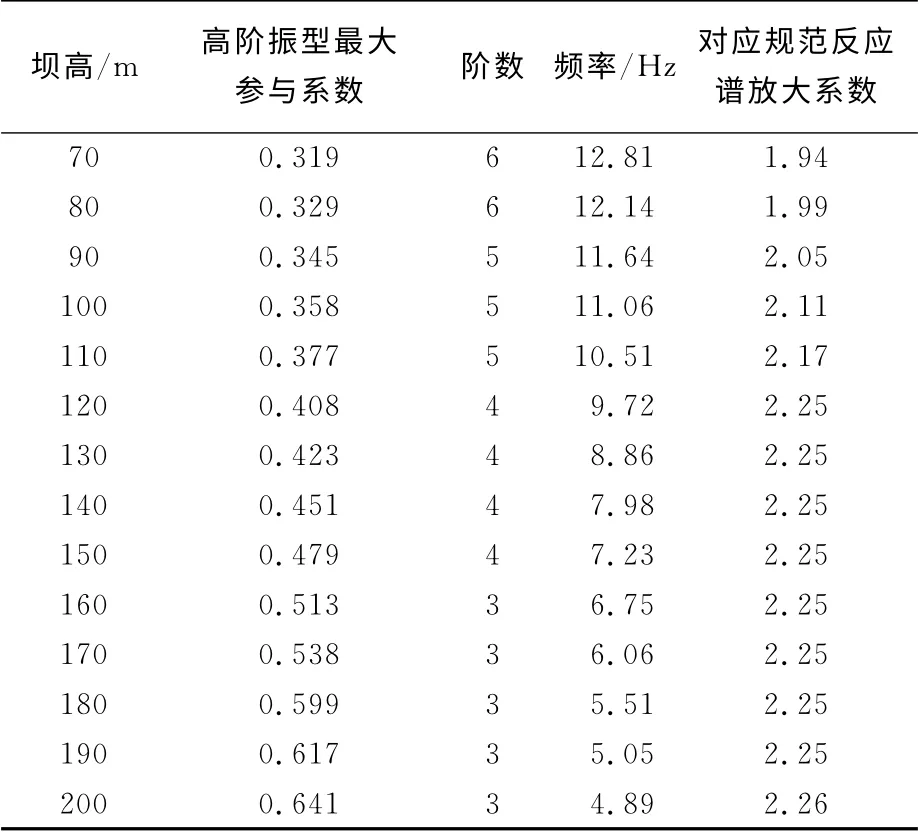
表2 70~200m 坝体的高阶振型最大参与系数及其对应于规范反应谱放大系数Tab.2 Participation factors of models of 70-200mdams and their amplifications to response spectrum

图1 坝体一阶振型及最大参与系数的高阶振型图Fig.1 The first order model shapes and higher order model shapes of dams
由于高坝的高阶振型参与系数增加,根据振型叠加法,高坝的坝头部是振动分析的关注部位.
2.2.2 坝体动水压力分析 对70~200m 重力坝地震作用下的动水压力进行分析,为便于比较,现将流固耦合与附加质量模型得到的动水压力值及Westergaard公式解析解绘成归一化曲线,如图2所示(y=坝高/最大水深;x=动水压力值/Westergaard最大解).表3给出5 种坝高的Westergaard最大解与流固耦合模型动水压力最大值的比较,以及流固耦合模型动水压力最大值出现在坝体上的部位.结合图2与表3分析可知,对于70~100 m 的低坝,Westergaard公式解与流固耦合模型所得上游坝面动水压力相比,在坝体上部略有偏小,下部偏大.坝踵处动水压力Westergaard解较流固耦合模型计算结果偏大约16%;对于160~200 m 的高重力坝而言,Westergaard解与流固耦合结果差别较大,体现出Westergaard解上部偏小、下部严重偏大的现象.如表3所示,随着坝高的增加,动水压力最大值较Westergaard最大解降低幅度有所增加,这种关系可以用线性函数表示:
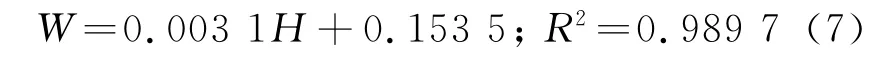
式中:H为坝高,W为流固耦合模型算得动水压力最大值较Westergaard最大解降低的百分比,R2为相关系数.
流固耦合模型动水压力最大值出现的位置也会随着坝体高度逐渐升高.在70 m 坝体动水压力最大值出现在距离坝踵上部5.4 m 处,而160 m 与200m 高坝的动水压力最大值出现在坝高的40%左右.这也可以用线性函数良好拟合,其表达式为

式中:D为流固耦合模型算得动水压力最大值出现的位置相对于坝底的高度.
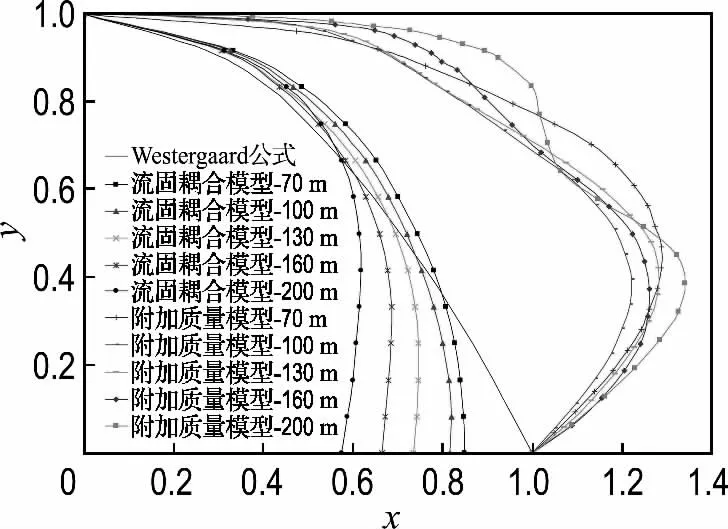
图2 5种高度坝体动水压力归一化比较Fig.2 Comparison of normalized hydrodynamic pressures from different heights of dams

表3 不同坝体动水压力最大值与Westergaard最大解的比较及出现最值部位Tab.3 Comparison of Westergaard solutions and hydrodynamic pressure maximums from different heights of dams and positions of maximums
由作者以往的动水压力模型试验[19]成果可知,高重力坝的动水压力试验结果与流固耦合模型计算结果相一致,与附加质量模型结果有较大差别.附加质量模型结果较动水压力试验结果偏大,可知其模拟动水作用有所夸大;李德玉等[20]通过动水压力模型试验研究也得出相同的结论.结合表3、图2及式(7)和(8),可以推断,70m 左右高度的中低重力坝计算动水压力用Westergaard公式能够近似反映真实情况,对于160m 以上的高坝来说误差较大,用流固耦合模型较为能够反映工程实际.这是由于200m 高坝相对于70 m 高的中低坝,其坝体的柔度有所增加(几何柔度也增加),导致坝腰部位受动水压力影响较大.Westergaard 公式表示动水压力最大值出现在大坝底部,动水压力分布也随着坝高的增加被严重夸大.
基于Westergaard公式推导出的附加质量模型因其计算简单、易于采用及偏于安全等因素,至今普遍被工程界所接受采纳.在地震条件下弹性坝体的加速度沿坝高有放大作用,导致了附加质量模型在整个上游面的动水压力明显大于Westergaard公式解与流固耦合结果,尤其在2/3坝高以上的部分.可见,采用附加质量模型计算弹性坝体的动水压力是被明显夸大的,这与本文作者[19]及其他学者[20-21]的实验结果分析相吻合.
2.2.3 位移分析 地震作用下5种高度重力坝顶上-下游向最大位移见表4.可以看出,无论是流固耦合模型还是附加质量模型坝顶上-下游向最大位移都随着坝体高度的增加而增大,且上游及下游方向最大位移的增幅较为一致.从两种模型的角度来看,附加质量模型的坝顶最大位移要明显大于流固耦合模型结果.对于200m 级的高重力坝,流固耦合模型与附加质量模型坝顶上游向的最大位移分别为34.81mm 和48.99mm,由此可知,两种模型模拟库水作用随着坝高的增加而差别越发明显,附加质量模型算得坝体位移反应有些夸大.图3给出不同高度坝体两种模型上游面位移包络图.由图可知,地震作用下,附加质量模型上游向(图3中负方向)最大位移在整个坝体高度上都比流固耦合模型大;对于100~200m级中高坝体,附加质量模型下游向(图3中正方向)位移反应与流固耦合模型不同,上部偏大,中下部偏小,而流固耦合模型坝体的上游向最大位移沿坝体高度增加十分均匀.
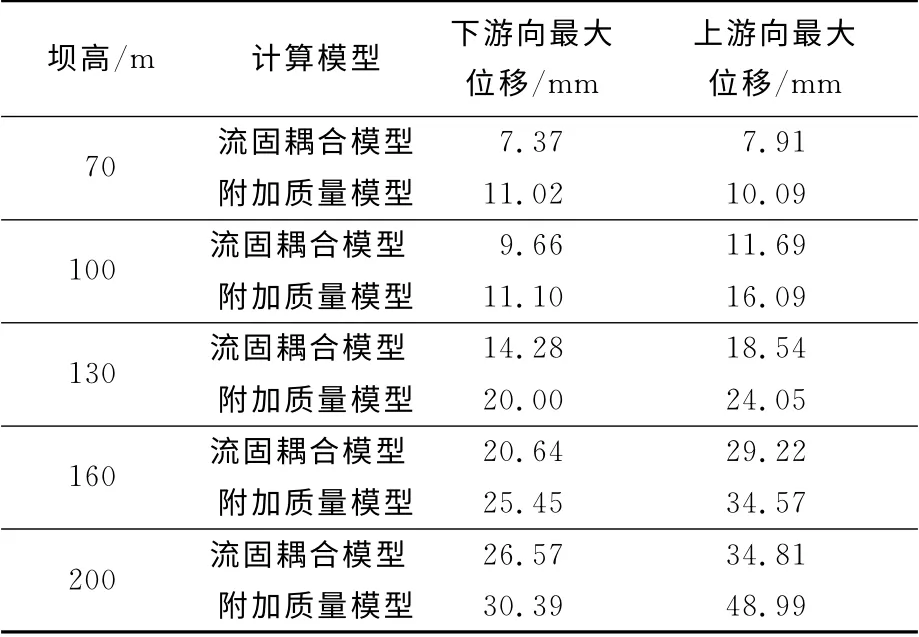
表4 不同工况下坝段坝顶的上-下游向位移Tab.4 Displacements in upstream and downstream on top of dams under different cases
2.2.4 加速度响应分析 地震作用下,流固耦合与附加质量两种模型算得5种高度坝体的峰值加速度沿坝高的分布如图4所示.两模型在坝颈部以下部分的加速度反应较为吻合,都出现了峰值加速度突增的趋势,可见重力坝的颈部是抗震的重要环节;两模型在坝颈部以上部分加速度的反应被放大得更加明显.坝顶峰值加速度被列于表5,可看出附加质量模型算得的所有高度坝体的坝顶峰值加速度均比流固耦合模型结果大,并且随着坝高的增加表现出显著增加的趋势.
2.3 柔性地基对低坝及高坝动水压力的影响分析
地震时柔性地基也是动水压力的重要影响因素.为充分考虑坝体及库区柔性地基的阻尼、惯性及动水波对动水压力的影响,计算中采用有质量地基并加入库底吸收系数.分别计算了70与200 m 高度坝体在柔性地基条件下上游面动水压力的分布情况.地基密度为2 700kg/m3,弹性模量为20 GPa,泊松比为0.25,库底吸收系数取为0.2,地基深度为3倍坝高.
如图5所示,分析两种坝高的计算结果发现,考虑地基(柔性基岩)和不考虑地基与坝体及库水相互作用时,坝体的反应因高度不同而有所差异.当坝高为70 m 时,不考虑地基与坝体及库水相互作用的最大动水压力为94.609kPa,出现在5.4m的高程处;考虑地基作用的最大动水压力出现在8.6 m 高程处,其值为88.812kPa;当坝高为200m 时,考虑与不考虑柔性地基作用的动水压力分别为206.693kPa和161.569kPa,出现的位置分别在约91m 和107m 的高程处.可见,地基对200m 级高坝及库水作用的影响非常明显,不但使动水压力最大值降低了21.7%,还把最大影响部位升高了17.5%,足见其在计算坝体与库水相互作用时不可忽略;对于70m 高的重力坝,考虑柔性地基作用时动水压力分布较不考虑地基作用差别很小,最大值减小约6.5%,最值出现部位基本相同,所以,在计算70m 及以下高度的重力坝坝体与库水相互作用时地基作用可以不用考虑.

图3 每种高度坝体两种模型上-下游向位移分布的比较Fig.3 Comparison of displacements in upstream and downstream on two models of dams of every height

图4 每种高度坝体两种模型峰值加速度沿坝高分布的比较Fig.4 Comparison of PGA along height on two models of dams

表5 每种高度坝体两种模型坝顶峰值加速度Tab.5 PGA on top of two models of dams of every height
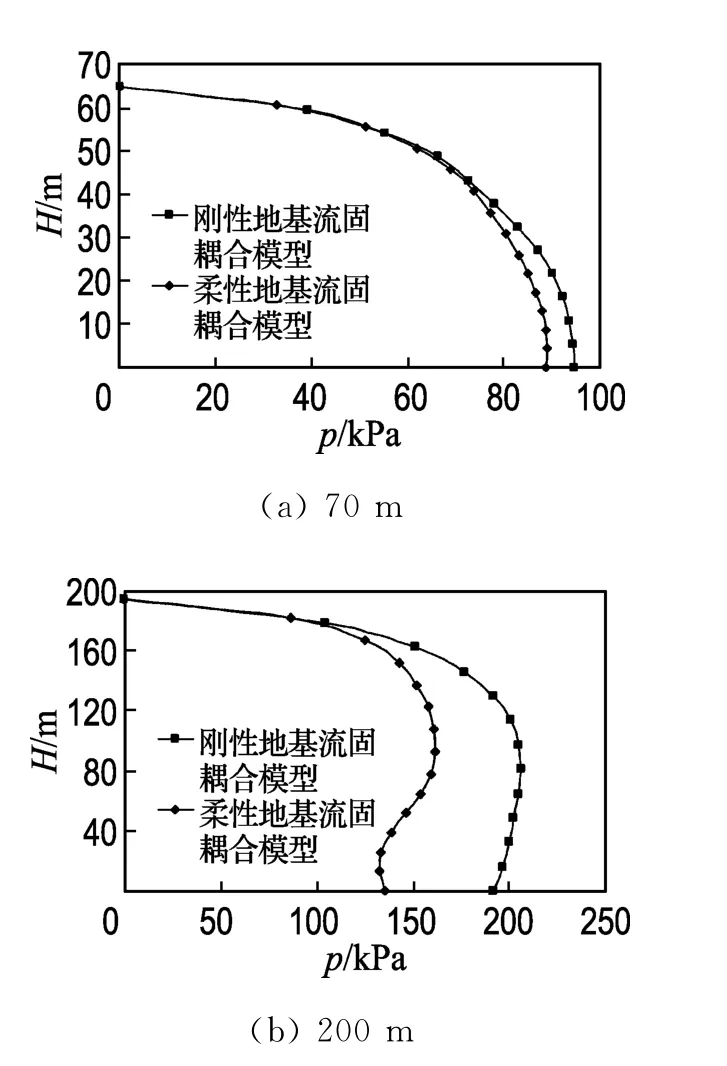
图5 70m 和200m 高度坝体有无地基的动水压力分布比较Fig.5 Comparison of dams hydrodynamic pressure with and without foundations in height of 70m and 200m
3 结 论
(1)满库时坝体基频较空库时有所降低,而且高坝比低坝降低得更多,说明震动时库水对高坝动力响应的影响更大;同高度附加质量模型坝体基频较流固耦合模型偏小,说明随着坝高的增加附加质量模型模拟库水对坝体作用较流固耦合模型有明显的夸大作用.
(2)Westergaard公式解析解较流固耦合模型动水压力值在坝体上部略偏小,而下部偏大,坝体越高,偏大越严重;流固耦合模型动水压力最大值出现于上游面位置且随坝高的增加逐渐升高.结合以往动水压力模型试验研究结果,说明采用流固耦合模型模拟库水对坝体的作用更符合真实情况;相比于Westergaard公式及流固耦合模型,弹性坝体的附加质量模型算得的动水压力在整个坝面上均被夸大,坝体越高,其上部所受动水压力被夸大得越严重.
(3)坝顶上-下游向最大位移都随着坝高的增加而增大;附加质量模型的坝顶最大位移明显大于流固耦合模型的位移反应,且对于160~200m的高坝而言,这种差异尤为显著.
(4)附加质量模型较流固耦合模型算得各个坝体加速度反应在坝颈部以下部分较为吻合,在坝颈部位均出现了峰值加速度突增的趋势,在坝颈及以上部位,两种模型的峰值加速度被放大得更为明显,可见重力坝的颈部是抗震的重要环节.随着坝高的增加附加质量模型坝顶峰值加速度却表现出增加的趋势,这造成了高坝顶部峰值加速度较流固耦合模型被明显夸大的情况.
(5)通过对高低重力坝是否考虑柔性地基对坝体与库水相互作用影响的分析可以得出,地基对200m 级高坝及库水反应的影响非常明显,在计算高坝-库水相互作用时地基作用不可忽略;对于70m 高的中低坝,此时地基作用可以不用考虑.
综上所述,在研究坝体-库水相互作用的耦合问题时,对于70 m 左右高度重力坝,可以采用Westergaard公式计算动水压力,而对于160 m以上的中高重力坝采用流固耦合模型计算库水作用及坝体动力响应较为接近现实情况;对于弹性坝体而言,采用附加质量模型模拟库水作用无论坝体多高都会夸大坝体的动力反应.
[1] Westergaard H M.Water pressures on dams during earthquakes [J].Transactions of the American Society of Civil Engineers,1933,98(2):418-433.
[2] Chakrabarti P,Chopra A K.Hydrodynamic pressures and response of gravity dams to vertical earthquake component[J].Earthquake Engineering&Structural Dynamics,1972,1(4):325-335.
[3] Chakrabarti P,Chopra A K.Earthquake analysis of gravity dams including hydrodynamic interaction[J].Earthquake Engineering & Structural Dynamics,1973,2(2):143-160.
[4] Chopra A K.Earthquake response of concrete gravity dams [J].Journal of the Engineering Mechanics Division,ASCE,1970,96(4):443-454.
[5] Chopra A K,Gupta S.Hydrodynamic and foundation interaction effects in earthquake response of a concrete gravity dam [J].Journal of the Structural Division,1981,107(8):1399-1412.
[6] Chopra A K,Chakrabarti P.Earthquake analysis of concrete gravity dams including dam-waterfoundation rock interaction [J].Earthquake Engineering & Structural Dynamics,1981,9(4):363-383.
[7] Fenves G,Chopra A K.Effects of reservoir bottom absorption on earthquake response of concrete gravity dams [J].Earthquake Engineering &Structural Dynamics,1983,11(6):809-829.
[8] Darbre G R.Phenomenological two-parameter model for dynamic dam-reservoir interaction [J].Journal of Earthquake Engineering,1998,2(4):513-524.
[9] Dominguez J,Maeso O.Earthquake analysis of arch dams.II:Dam-water-foundation interaction[J].Journal of Engineering Mechanics,1993,119(3):513-530.
[10] Maeso O,Aznarez J J,Dominguez J.Effects of space distribution of excitation on seismic response of arch dams [J].Journal of Engineering Mechanics,2002,128(7):759-768.
[11] Maeso O,Aznarez J J,Dominguez J.Threedimensional models of reservoir sediment and effects on the seismic response of arch dams [J].Earthquake Engineering & Structural Dynamics,2004,33(10):1103-1123.
[12] Brathez H A,Heilbron C H.Discussion of water pressures on dams during earthquakes [J].Transactions of the American Society of Civil Engineers,1933,98(2):434-470.
[13] 杜修力,王进廷.动水压力及其对坝体地震反应影响的研究进展[J].水利学报,2001,46(7):13-21.DU Xiu-li,WANG Jin-ting.Review of studies on the hydrodynamic pressure and its effects on the seismic response of dams[J].Journal of Hydraulic Engineering,2001,46(7):13-21.(in Chinese)
[14] DU Xiu-li,WANG Jin-ting.Seismic response analysis of arch dam-water-rock foundation systems[J].Earthquake Engineering and Engineering Vibration,2004,3(2):283-291.
[15] 杜修力,王进廷.拱坝-可压缩库水-地基地震波动反应分析方法[J].水利学报,2002,47(6):83-90.DU Xiu-li,WANG Jin-ting.Analysis method for seismic response of arch dam-compressible waterfoundation systems [J].Journal of Hydraulic Engineering,2002,47(6):83-90.(in Chinese)
[16] 林 皋,杜建国.基于SBFEM 的坝-库水相互作用分析[J].大连理工大学学报,2005,45(5):723-729.LIN Gao,DU Jian-guo.Analysis of dam-reservoir interaction based on SBFEM [J].Journal of Dalian University of Technology,2005,45(5):723-729.(in Chinese)
[17] 杜建国.基于SBFEM 的大坝-库水-地基动力相互作用分析[D].大连:大连理工大学,2007.DU Jian-guo.The dynamic interaction analysis of dam-reservoir-foundation based on SBFEM [D].Dalian:Dalian University of Technology,2007.(in Chinese)
[18] Parrinello F,Borino G.Lagrangian finite element modelling of dam-fluid interaction: Accurate absorbing boundary conditions[J].Computers &Structures,2007,85(11-14):932-943.
[19] 王铭明,陈健云,范书立.重力坝地震动水压力的试验研究[J].水电能源科学,2012,30(5):51-53,89.WANG Ming-ming,CHEN Jian-yun,FAN Shu-li.Experimental study on earthquake hydrodynamic pressure of gravity dam [J].Water Resources and Power,2012,30(5):51-53,89.(in Chinese)
[20] 李德玉,张伯艳,王海波,等.重力坝坝体-库水相互作用振动台试验研究[J].中国水利水电科学研究院学报,2003,1(3):216-220.LI De-yu,ZHANG Bo-yan,WANG Hai-bo,etal.A shaking table model test on dam-reservoir interaction of gravity dam [J].Journal of China Institute of Water Resources and Hydropower Research,2003,1(3):216-220.(in Chinese)
[21] 宫必宁.重力坝地震动水压力试验研究[J].河海大学学报,1997,25(1):98-102.GONG Bi-ning.Experimental study on earthquake hydrodynamic pressure of gravity dam [J].Journal of Hohai University,1997,25(1):98-102.(in Chinese)

