基于性能可靠性约束的智能液压泵节能优化

黄伯超 王少萍 孟奕璇 石 健

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

军用飞机对高速、高机动性能、小自重、大有效载荷和高可靠等综合性能的迫切需求，促使机载液压系统向高压化、大功率、变压力、智能化等方向发展［1］.高压大功率智能泵源可根据不同飞行状态的需求实时调节流量、压力输出，以减少机上无效功率的产生、降低系统的发热量.为实时适应负载需求，智能液压泵需在4种工作模式间来回切换，应保证其在各种工况下均满足系统性能要求，因此需要对其作性能可靠性分析.

性能可靠性分析大多基于性能退化作研究，通过观察退化过程直接由失效机理建模，使可靠性统计推断更趋准确可信［2］.但当研究对象工况可变时，某工况下的性能退化规律不适用全局，由此引入多阶段任务系统(PMS，Phased Mission System)可靠性分析方法，其应用通常基于组合分析法和马尔可夫分析法［3－4］.为提高 PMS 的适应性，文献［5］提出将PMS划分为静态和动态两级、各用其法，最后用模块联合概率法综合.为减少PMS求解的复杂度，许多学者尝试简化的PMS方法［3－7］，主要思想是用某种方法将多阶段任务转化为几个相互独立的单阶段任务，分别建立可靠性模型，再用条件概率法综合为总的可靠性模型.

机载智能液压泵源是典型的PMS，根据负载需求的不同，有压力、流量、功率和负载敏感4种工作模式，各工作模式下的控制信号可调，工作模式和控制信号的选择取决于任务需求［8］.智能液压泵的性能可靠度是指其在飞行任务剖面规定的工况条件下、在任务时间的所有阶段均完成规定的模式切换功能和液压输出功能的概率.

本文从性能设计的角度出发，分析智能泵的性能退化影响因素，建立各工作模式下的性能可靠性模型;以节能为目标、性能可靠性指标为约束，优化设计液压泵关键参数，在满足性能可靠性指标的前提下使智能液压泵工作效率最高.

1 智能液压泵的结构模型

智能液压泵实现智能控制的原理是:根据负载对压力、流量的需要实时控制柱塞泵的斜盘倾角，通过改变瞬时排量来调节泵的流量、压力输出，可见斜盘变量机构是其功能实现的关键所在.将A4V型柱塞泵的调压阀替换成调压伺服阀，即可成为智能液压泵.A4V泵的斜盘变量机构是典型的阀控对称缸结构，其斜盘倾角γ可表示为

其中，Kq为调压伺服阀流量放大系数;Ke为斜盘变量机构总流量压力系数;AC为随动活塞截面积;L为变量油缸轴线到斜盘转动轴的距离;xV为调压伺服阀阀芯位移;VC为变量油缸总容积;βe为液压油等效体积弹性模量;Vp为干扰力矩压力系数;ps为泵出口压力)为斜盘变量机构的液压固有频率和阻尼比，I为斜盘变量机构总惯量.

柱塞泵的理论输出流量Qt为

其中，n为柱塞泵转速;Dγ=d qt/dγ为关于斜盘倾角γ的排量梯度;qt为柱塞泵的理论排量.实际计算表明:在γ变化范围内，Dγ近似为常值的最大误差不超过5%.柱塞泵的出口压力ps为

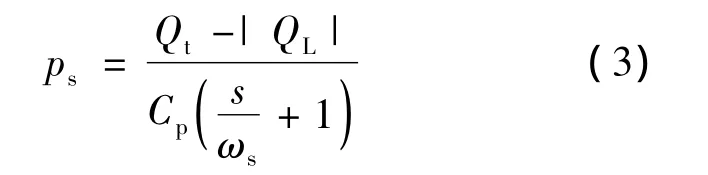
其中，QL为负载流量;Cp为液压泵内泄漏系数;ωs=βeCp/Vs为容积滞后转折频率，Vs为泵出口压力腔的容积.

综合式(1)～式(3)，加入控制器及伺服阀，可得柱塞泵在4种工作模式下的闭环方框图.从动态响应特性看，智能泵的流量模式与功率模式是一致的，压力模式与负载敏感模式是一致的，可将4种工作模式重新划分为流量控制(包括流量模式和功率模式)和压力控制(包括压力模式和负载敏感模式)2类模式，如图1和图2所示.

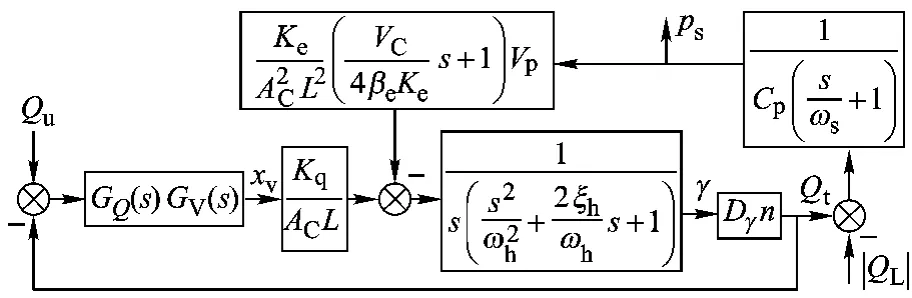
图1 柱塞泵在流量控制类模式下的闭环方框图

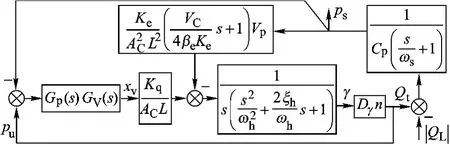
图2 柱塞泵在压力控制类模式下的闭环方框图

因控制器特征频率比柱塞泵其他环节的大得多，本文视其为比例环节，即GQ(s)=KQ，Gp(s)=Kp;GV(s)为调压伺服阀传递函数，有

其中，KV为伺服阀增益;ωV，ξV分别为伺服阀的特征频率和阻尼比.

1.1 流量控制类模式的闭环传递函数

由图1求得流量控制类模式由Qu到Qt的闭环传递函数，并利用实际参数值在累积误差小于10%的前提下简化，得

其中，T为一阶惯性环节的时间常数;ωQ，ξQ分别为二阶振荡环节的转折频率和阻尼比，有

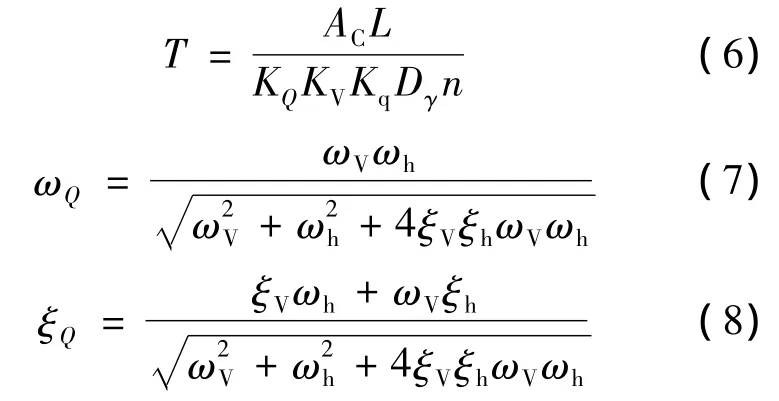
在流量控制类模式中，由于一阶惯性环节占绝对主导地位，二阶振荡环节对系统响应的影响微乎其微，系统快速性取决于后者，其动态响应无超调，因此后面不再对ωQ和ξQ作进一步分析.

1.2 压力控制类模式的闭环传递函数

根据图2求得压力控制类模式由pu到ps的闭环传递函数，并利用实际参数值在累积误差小于10%的前提下简化，得

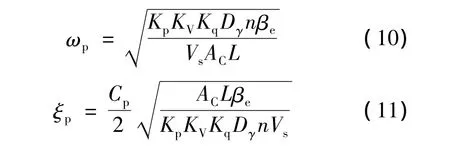
其中，ωp，ξp分别为压力控制类模式闭环传递函数的转折频率和阻尼比，有

2 智能液压泵性能影响因素分析

2.1 流量控制类模式的性能影响因素分析

在流量控制类模式下，表征智能液压泵动态性能的指标是T，反映了液压泵的惯性，其数值越小，表明惯性越小、响应也就越快，故可用1/T作为指标来判断系统响应的快速性.

根据式(6)，将流量控制类模式的性能影响因素分析列表如表1所示.

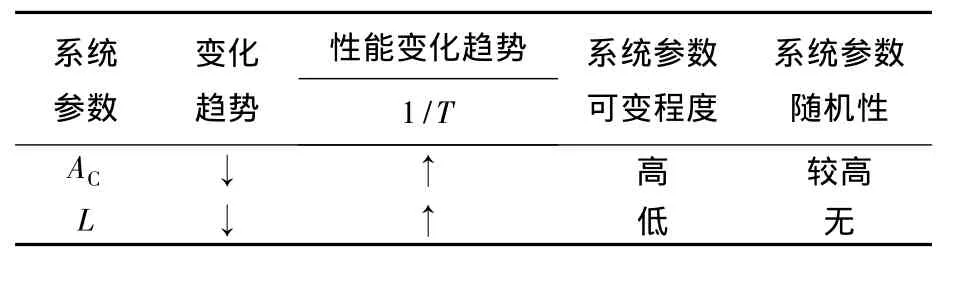
表1 流量控制类模式性能影响因素分析

表1中，系统参数的可变程度是指柱塞泵在设计时参数变化的程度:①AC减小，将使1/T增大，考虑到加工误差和使用磨损，其截面积可用正态分布表征;②L的影响:由于柱塞泵空间尺寸的限制，在斜盘变量机构最佳布局的前提下其数值没有太大的可变余地，故L可视其为定值.

其他参数在伺服阀选定后和液压泵总体设计后不再变化，故不作分析.因此，本文选择AC作为影响流量控制类模式性能可靠性的参数.

2.2 压力控制模式下的性能影响因素分析

在压力控制类模式下，表征智能液压泵动态性能的指标有:ωp反映液压泵动态响应的快速性，在合理范围内其数值越大越好;ξp体现液压泵动态响应的超调量，根据国内外柱塞泵相关标准中对压力响应快速性和超调量不大于20%的要求［9］，必须满足 0.46≤ξp＜1.

根据式(10)和式(11)，将压力控制类模式的性能影响因素分析列表如表2所示.

表2 压力控制类模式性能影响因素分析

表2中可变参数说明如下:①AC减小，将使ωp增大、ξp减小;②Cp增大将使ξp呈比例增大，而对ωp无影响，但增大内泄漏将降低泵的工作效率.因此，在压力控制模式下选择AC和Cp为性能参数.

2.3 智能液压泵的任务剖面分析

智能液压泵的模式切换和控制信号均由飞机的飞行任务剖面决定，本文采用某型战斗机的飞行统计数据［1］研究典型飞行剖面，根据模式切换原则和控制信号生成机理，给出液压泵的任务剖面(图3)，为性能可靠性模型综合提供依据.

图3中的工作模式选择体现了以下原则:

1)负载对压力要求不高，需高速或恒速运动时，采用流量工作模式，适用于起飞、着陆阶段;

2)负载对压力和流量要求均较高时，采用压力工作模式，适用于爬升、下降阶段;

3)负载对压力、流量均要求很高，功率超限或负载要求恒功率输出时，采用功率工作模式，此时优先保证压力输出，适用于突击、战斗阶段;

4)负载对压力、流量均要求不高时，采用负载敏感工作模式，此时工作效率最高，适用于巡航、搜巡阶段.

另外，为智能液压泵选择工作模式时需用到智能液压泵基本参数，现将其列出，如表3所示.

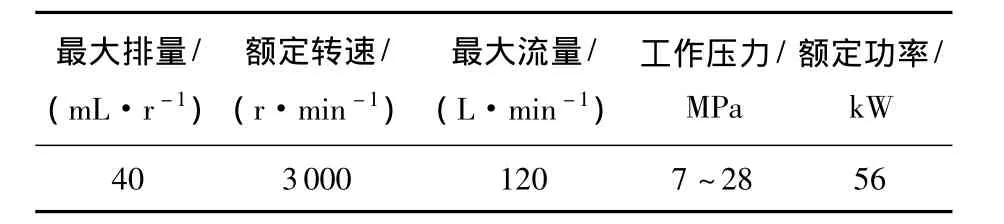
表3 智能液压泵基本参数

图3 智能液压泵模式切换原理

3 基于节能的智能泵性能可靠性建模

3.1 智能液压泵性能可靠性建模

引入随机变量x，y和z，定义如下:

其中，K=KVKqDγ/L.

式(12)～式(14)中的Cp和βe与ps相关，并非随机变量.n和AC的取值具有明显的随机特性，符合正态分布且相互独立，故x，y和z亦服从正态分布.

智能泵的性能可靠度分别为

其中，xu，yu为参数设计要求值的下限.

3.2 基于任务剖面的液压泵性能可靠性建模

由图3可知，智能液压泵工作剖面是典型的多阶段任务.设S={Q，p}表示全周期任务，其中Q表示流量模式，其性能参数为x;p表示压力模式，其性能参数为y，z.智能泵的阶段任务是S1，S2，…，Sl，各阶段工作时间为 t1，t2，…tl(l为任务阶段总数).智能泵在第i个阶段的故障概率为

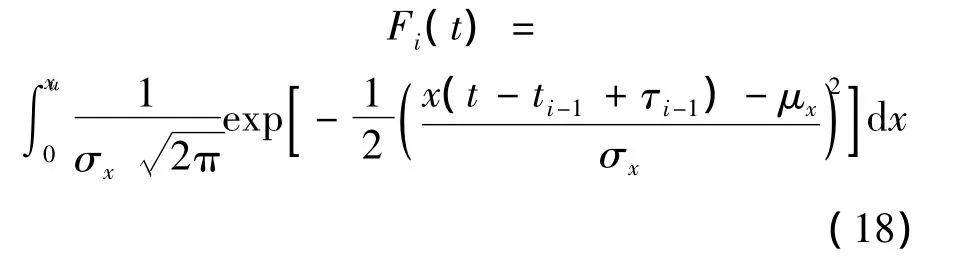
其中，τi－1=ti－ ti－1+ τi－2;τ0=0.由累积损伤理论，得任意阶段故障概率密度为

采用极大似然函数可以得到式(19)中的参数，并得到多任务阶段的性能可靠度指标为

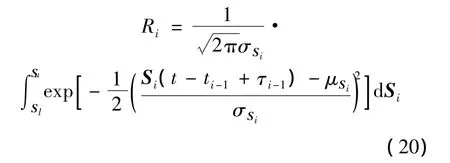
3.3 基于节能的智能液压泵优化设计

智能泵设计时，其工作效率的提高和可靠性的提升是相互矛盾的，故需进行节能和可靠度的优化设计.本文以智能泵工作效率η最大作为目标函数，各阶段可靠度指标为约束条件，得

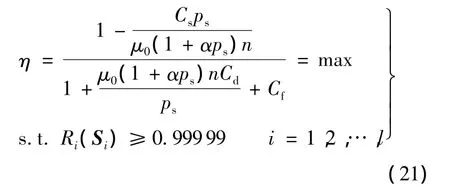
其中，Cs为滑流系数;μ0为液压油标称动力粘度;α为粘度-压力系数;Cd为阻尼系数;Cf为柱塞-缸孔间的动摩擦系数.

采用粒子群算法［10］进行参数优化，得到表4所示的优化智能泵结构尺寸.

表4 智能泵优化设计结果

根据智能液压泵各模式控制信号的生成原则生成各阶段的控制信号，与负载要求一起形成任务剖面，利用优化得到的结果和任务剖面各参数，可得到智能液压泵性能不可靠度曲线如图4所示.

图4 智能泵性能不可靠度曲线

由图4可知，1/T的可靠度为常值，即不受工况影响;ωp，ξp的可靠度主要受 ps影响，均为 ps越大可靠度越高，且影响较明显.但ξp可靠度受液压油压力变化的影响稍弱于ωp，这是因为ps升高导致弹性模量升高的同时亦增加其粘度，从而降低Cp，部分抵消了弹性模量增加的影响.在全任务剖面内，所有性能参数的可靠度均满足设计要求，且变动范围均未超过1个数量级，说明优化过程充分利用了可用空间，证明本文性能可靠性分析和优化是符合智能泵实际工况的.

同工况下，对比分别采用恒压变量泵和智能液压泵供压的液压系统工作效率，如图5所示.

图5 智能泵与恒压泵节能对比

图5中计算系统η时假设负载压力流量随任务剖面发生变化，而执行系统(含管道、作动器和阀等)的结构特性保持不变.由图5可知，两种系统只有在最大压力最大流量工况下η才相等;大流量会导致η急剧下降，这是因为大流量带来更大的传输损失;系统在小压力工况下时，智能泵系统的η明显高于恒压泵系统，特别当系统在小流量小压力工况下时，智能泵系统切换至负载敏感模式，此时其节能效果最为佳，并且由于系统在此工况下持续时间最长，节能效益尤为可观.在全任务剖面内求两种系统的平均效率，所得恒压泵系统的数值为73.3%，智能泵的数值为89.1%，两者差距高达15.8%，证明了智能液压系统在节能方面的优越性.

4 结 束 语

本文提出基于节能多模可靠性模型的分析方法，建立智能泵2类工作模式的传递函数模型，提炼智能泵性能的影响因素，构建性能可靠性模型.考虑实际飞行剖面，基于累积损伤理论构建多阶段任务可靠性模型，以工作效率最高为目标、性能可靠性指标为约束，优化设计智能泵结构参数.仿真结果表明:基于性能可靠性约束的智能泵节能优化方法更有效，优化后的智能泵系统相比传统恒压泵系统，其平均效率可提高15.8%.

References)

［1］陈斌，王占林，裘丽华.机载液压系统的主要发展趋势［J］.航空学报，1998，19(7增刊):S1－S6 Chen Bin，Wang Zhanlin，Qiu Lihua.Main developmental trend of aircraft hydraulic systems［J］.Acta Aeronautica et Astronautica Sinica，1998，19(7Supplement):S1 － S6(in Chinese)

［2］ MeekerW Q，Hamada M.Statistical tools for the rapid development＆ evaluation of high-reliability products［J］.IEEE Transactions on Reliability，1995，44(2):187 －198

［3］ Alam M，Song M，Hester S L，et al.Reliability analysis of phased-mission systems:a practical approach［C］//2006 Proceedings Annual Reliability and Maintainability Symposium.NB:IEEE，2006:551 －558

［4］ Ma Y，Trivedi K S.An algorithm for reliability analysis of phased-mission systems［J］.Reliability Engineering and System Safety，1999，66:157 －170

［5］ Ou Y，Dugan J.Modular solution of dynamic multi-phase systems［J］.IEEE Transactions on Reliability，2004，53(4):498 －503

［6］ Wang Chaonan，Xing Liudong，Levitin G.Competing failure analysis in phased-mission systems with functional dependence in one of phases［J］.Reliability Engineering and System Safety，2012，108:90－99

［7］ Xing L，Amari SV.Recursive algorithm for reliability evaluation of non-repairable phase mission systems with binary elements［J］.IEEE Transactions on Reliability，2012，61(2):533 － 542

［8］ Huang Bochao，Wang Shaoping.Adaptive mode switch of intelligent hydraulic power supply system［C］ //2011 International Conference on Fluid Power and Mechatronics.Beijing:IEEE，2011:844－849

［9］ SAE-AS19692 Pumps，hydraulic，variable flow，general specification for［S］

［10］ Eberhart，R C，Kennedy J.A new optimizer using particle swarm theory［C］ //Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya:IEEE，1995:39－43