储液容器内液体晃动问题的动力学建模与模拟
贾善坡,赵友清,许成祥
(长江大学 城市建设学院,湖北 荆州434023)
0 引言
目前,充液系统液体晃动问题研究进一步热化,主要表现在:微幅晃动问题研究,非线性大幅晃动问题研究,液固耦合晃动及考虑弹性壁的液固耦合晃动问题研究,液体晃动理论及等效力学模型研究等.液体晃动问题的解法主要有解析法和数值分析法. 解析法主要是采用Bessel 方程、Fourier 方程及Laplace 变换求解特殊形状、边界的线性流固耦合问题;数值计算方法同时将流体域和固体域离散化求解,如有限单元法、有限差分法、边界元法和边界积分法等.而对于复杂的三维晃动问题求解多使用有限单元法.具体代表如下:Housner[1]假设储液罐壁是刚性的且置于刚性基础上,使用Laplace 方程求解矩形和圆柱形储液罐的基本模态. Wang Wei 等[2]使用FEM 分析了储罐在不同边界条件下液体晃动模态.贾善坡、郑建华等[3-4]利用有限元软件ANSYS 分析了固液耦合系统的模态及动态响应. 赵晓磊等[5]利用有限元软件ADINA 对大型储液罐进行了模态分析.包光伟等[6]采用VOF 方法对储箱内液体晃动进行了数值模拟分析. 尚春雨等[7]利用FLUENT 方法分析了液体晃动问题.刘富等[8]采用SPH 方法成功模拟了三维液体晃动产生的波浪翻卷. 李青等[9]推导出任意三维容器内液体晃动的等效力学模型,并应用FLOW-3D 分析软件验证了该模型的正确性.
笔者使用声学单元描述流体,流体自由表面单元“削皮”成膜单元,两者通过弹簧单元连接,实现了位移与应力的兼容,并将计算得到的晃动模态及频率与解析解对比,结果表明该方法是可行的,最后使用该方法分析了矩形储液罐在不同液体高宽比时,其晃动频率与液体深度、宽度的关系,并从中获得矩形储液罐液体晃动的一般规律.
1 液体晃动控制方程
1.1 声学方程
流体视为声学介质,将其作为弹性介质分析其晃动动力特性,对于可压缩、无黏性和小扰动流体,考虑其材料阻尼的微幅运动平衡方程为[10]
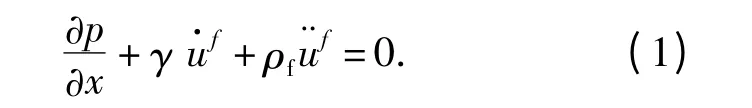
式中:p 是流体动压;x 是流体质点的空间坐标;u·f是流体质点的速度;u¨f是流体质点加速度;ρf是流体的密度;γ 是体积曳力.
假设流体介质是可压缩、无黏性和线性的,计算流体动压时考虑体积模量影响,其本构方程为:
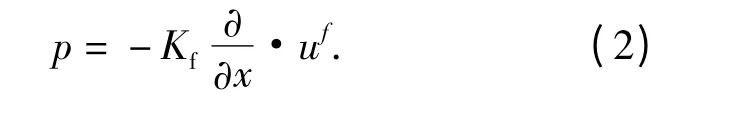
式中:Kf是流体的体积模量.
对可压缩、无黏性流体,式(2)可写为只含体积模量和体积应变线性方程:
p= -KfεV. (3)
式中:εV是流体体积应变.
1.2 流体动力学方程
对无黏性、可压缩和小扰动的流体,由流体域Vf内场方程联立消去密度变量ρ 和流动速度vi得到以压力扰动p 为场变量的波动方程:
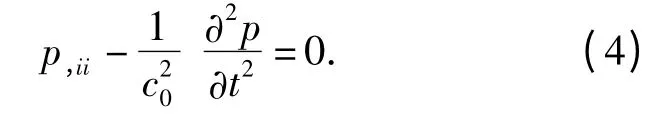
式中:c0为流体中的声速.
假设储液罐壁为刚性且储液罐放置在刚性基础上,则可得到刚性边界条件方程:

式中:n 为流体边界外法线向量.
流体自由液面边界条件方程:
2 有限元模型与数值方法
对流体域采用流场压力p 作为基本变量,构造插值函数Nk(x,y,z),则流体域压力分布为

式中:n 为流体单元节点总数.
对波动方程(4)和边界条件方程(5)、(6)利用加权余量的Galerkin 法解方程:

式中:Vf为流体域;sb为刚性边界面;sf自由液面边界.
将式(7)代入式(8),并考虑δp 的任意性,得到流体自由晃动有限元方程:+Kfp=0. (9)
式中:Mf为流体质量矩阵;Kf流体刚度矩阵.
假定方程(9)解的形式p=φsinω(t-t0)并反代入,得到液体自由晃动的特征方程:

式中:ω1,ω2,…,ωn为n 个固有频率;φ1,φ2,…,φn为其对应的n 个固有振型.
考虑到液体晃动系统自由度多且需要获得大量固有模态,为提高其计算效率,采用兰索斯法提取特征值.Lanczos 程序运行一系列迭代步,对每一次运行经过谱变换:
[M](K-σ[M])-1[M]{Φ}=θ[M]{Φ}. (11)
式中:σ 为偏移值;θ 为特征值;{Φ}为特征向量.
方程(11)将快速收敛到所需要的特征值.方程(10)与方程(11)中,特征向量φ 与{Φ}是一致的,但固有频率值ω 与θ 具有如下关系:

程序每运行一次Lanczos 命令生成一个Krylov 子空间序列,经过一系列运算步计算出最近似的子空间特征向量. 理论上,Lanczos 的基本流程可以确定简单的特征值,然而对大型矩阵特征值问题显得太昂贵. 因此,笔者采用分块Lanczos法[12],通过创建一个正交向量块,并利用每次Lanczos 步中的块的大小增加Krylov 子空间的维数,这样不仅可以自动计算大型矩阵特征值,还大大提高了计算效率.
3 数值算例
分析模型为一正方形截面的刚性储液罐,其底部固定,边长B =2 m,液面深度H =3 m,流体密度ρ=1 000 kg/m3,声速c0=1 435 m/s,液体的体积模量2.06 GPa,重力加速度g=9.8 m/s2.
建立三维储液容器液体晃动模型. 假设液体是无黏性、不可压缩、无旋的理想液体,罐体锚固于刚性地基上,液体晃动为小波动.对液体域划分为下部流体及其顶部自由液面,其中流体部分采用声学单元AC3D8,顶部自由液面采用膜单元M3D4.在液体晃动问题中,重力作为恢复力是必不可少的,然而在声学单元中不允许直接定义均布重力荷载,为了解决这个问题,引入重力弹簧附加至流体自由液面各个节点. 声学单元仅有应力自由度,而弹簧单元仅有位移自由度,为了克服这种不兼容性,流体自由液面“削皮”成膜单元,膜单元没有弯曲刚度,通过“TIE”命令实现与声学单元的耦合.当液体晃动时,自由液面的每个微面均受到一个重力恢复力ρgA,A 为自由液面微面面积;其中取ρgA 的大小作为弹簧刚度(本例中流体横截面被225 个节点分割,). 另外,考虑到网格划分对结果的影响,据文献[11]知:空间步距Δx 需控制在Δx <λ/6 时,才能满足波动数值模拟的精度要求,即一个波长内一般不少于6 ~8个节点.
3.1 自由晃动结果分析
使用上述方法计算流体晃动频率结果如图1和图2 所示.从图中分析得到,流体自由晃动频率包括低频和高频两部分. 低频部分对应于流体自由晃动时分布在自由液面的动压力引起的自由液面波动;高频部分对应于流体内部动压力波动.由于本例划分网格时,在液体自由表面共布置了225 个节点,故分析中模态阶数取其前300 阶,其中前225 阶为晃动频率低频部分,最大值为第225阶ω=17.727 rad/s;晃动频率高频部分从第226 阶ω=785.20 rad/s 到第300 阶ω=9 331.70 rad/s.

图1 流体自由晃动的低频部分(1 ~70 阶)Fig.1 Low-frequencies part of liquid sloshing(1 ~70)
为了验证上述方法的准确性,首先计算出前9 阶液体晃动频率理论值,其次采用本文方法获得液体晃动前9 阶模态及频率,最后与文献[3]结果三者对比,如表1 所示.

图2 流体自由晃动的高频部分(226 ~300 阶)Fig.2 High-frequencies part of liquid sloshing(226 ~300)

表1 流体自由晃动频率计算结果比较Tab.1 Comparison of results for natural frequencies of liquid sloshing rad/s
由计算结果和理论解比较发现,误差较小,控制在5%以内,且所使用的算法比文献[3]所得结果更接近理论值,由此可见,本文声学模型算法的有效性和可靠性得到验证.
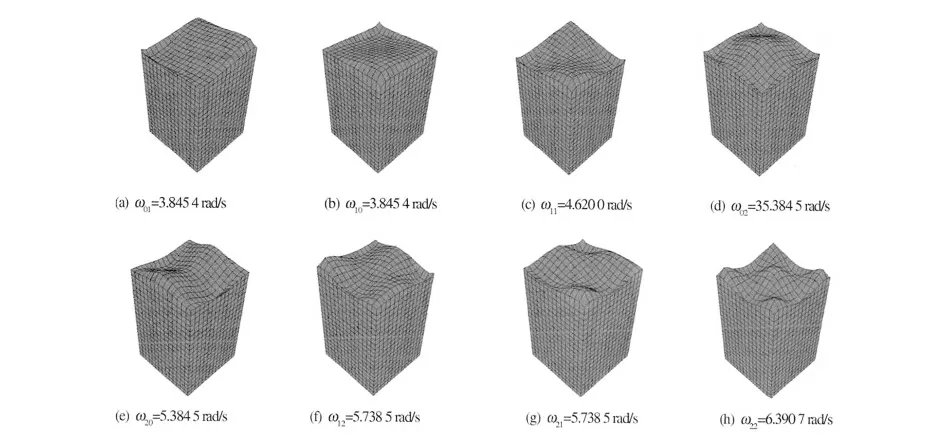
图3 流体自由表面波动模态图Fig.3 Shapes of liquid system corresponding to the sloshing mode
3.2 晃动频率与容器尺寸关系
通过声学模型有限元法计算储液罐液体晃动频率,研究储液罐液体在不同容器尺寸时(以容器截面为正方形为例)其晃动频率的变化规律.在讨论时,将液体深度H 作为一不变量,即液深H=3 m 恒定不变. 容器尺寸(正方形截面边长a)在a=1,2,3,4,5,6 m 时,分别获得前几阶自然晃动频率,取前4 阶自然频率绘出f-a 变化曲线如图4 所示.从图中看出:液体前4 阶晃动频率受储液罐体尺寸影响显著;随着储液罐尺寸a 的增大,液体的自然晃动频率均渐渐减小,可以说液体晃动频率与储液罐边长基本上保持反比例关系;在储液罐边长由1 m 变化至2 m 时,前4 阶晃动频率的变化率均较大,随后随着储液罐边长的增大晃动频率变化率较平缓.

图4 液体晃动频率与容器边长的关系Fig.4 Liquid sloshing frequencies versus the length of container
3.3 晃动频率与液体深度关系
用同样的方法研究储液罐液体晃动频率与储夜深度之间的变化规律.在讨论时,约定储液罐截面边长a 为一恒定量,即a =2 m. 储液深度H 为1,1.5,2,2.5,3,3.5,4,5,6 m 时,分别获得前几阶自然晃动频率,同样取前4 阶自然频率为例绘出f-H 变化曲线如图5.结果表明,第1 阶和第2阶频率在充液深度由H =1 m 至H =1.5 m 时变化较大;在液深H=2 m 时,晃动频率分别达到该阶段最大值3.838 2 rad/s 和4.617 9 rad/s,随后随着充液深度增大,频率基本无显著变化.对于第3 阶和第4 阶频率,在充夜深度变化期间其自然晃动频率基本无明显变化.总体来说,充液深度对液体晃动频率影响没有储液罐体尺寸对其影响显著.

图5 液体晃动频率与液体深度的关系Fig.5 Liquid sloshing frequencies versus the depth of liquid
4 结论
(1)由计算值与理论解及文献[3]结果对比可知,以ABAQUS 软件平台编制的分析程序对矩形储液罐三维晃动动力特性分析研究是可行的.分析过程中流体采用ABAQUS 特有的声单元,流体自由液面单元“削皮”成膜单元,通过弹簧单元连接两者,实现了位移与应力的兼容,使得计算结果精度更高,更接近理论值.
(2)流体自由晃动频率包括低频和高频两部分,低频部分对应于流体自由晃动时分布在自由液面的动压力引起的自由液面波动,高频部分对应于流体内部动压力波动;若要得到更多低阶频率需对横截面网格细分;流体晃动频率与储液罐尺寸基本上保持反比例关系;充液深度对流体体晃动频率影响没有储液罐体尺寸对其影响显著.
(3)利用该方法可计算任意复杂形状的三维晃动问题,但对流固耦合问题特别是流体-储液罐-地基三者耦合问题有待做进一步研究.
[1] HOUSNER G W.The dynamic behavior of water tanks[J]. Bulletin of Seismological Society of America ,1963,53(2):381 -389.
[2] WANG Wei,LI Jun-feng,WANG Tian-shu. Modal analysis of liquid sloshing with different contact line boundary conditions using FEM[J]. Science Direct,2008(317):739 -759.
[3] 贾善坡,许成祥,谭继可.矩形容器内液体三维晃动特性研究[J]. 水电能源科学,2012,30 (1):142-144.
[4] 郑建华,李金光,唐辉永. 立式圆柱形储液罐的三维液固耦合模态分析[J]. 化工设计,2012,22(1):25 -27.
[5] 赵晓磊,张荣花,张亮. 15 ×104m3浮放储罐的模态分析[J]. 大连民族学院学报,2009,11(1):71-73.
[6] 包光伟,王振强,张天翔,等.火箭推进剂液体晃动关机响应的数值仿真[J]. 宇航学报,2002,23(2):84 -88.
[7] 尚春雨,赵金城. 用FLUENT 分析刚性容器内液面晃动问题[J].上海交通大学学报,2008,42(6):953-956.
[8] 刘富,童明波,陈建平.基于SPH 方法的三维液体晃动数值模拟[J]. 南京航空航天大学学报,2010,42(1):122 -126.
[9] 李青,马兴瑞,王天舒.非轴对称贮箱液体晃动的等效力学模型[J].宇航学报,2011,32(2):242 -249.
[10] HKS. ABAQUS/Standard version 6.5 user’s manual[M]. Rhode Island,USA:Hibbit,Karlsson and Sorensen Inc. 2002.
[11]廖振鹏,工程波动理论导论[M]. 北京:科学出版社,2002.
[12]GRIMES R G,LEWIS J G,SIMON H D. A Shifted block lanczos algorithm for solving sparse symmetric generalized eigenproblems[J].SIAM Journal on Matrix Analysis and Applications,1994(15):228 -272.

