二模磁场中随机晶场作用混合自旋横向Ising模型的临界行为

丁直，晏世雷

（苏州大学物理科学与技术学院，江苏苏州 215006）

二模磁场中随机晶场作用混合自旋横向Ising模型的临界行为

丁直，晏世雷

（苏州大学物理科学与技术学院，江苏苏州 215006）

在有效场理论和切断近似的框架内，研究了二模磁场中随机晶场作用的混合自旋横向Ising模型的临界行为.在T-h相图中，晶场浓度对有序相的影响需要将二模磁场分段考虑；大的晶场和适当的晶场浓度有利于二级重入相变现象；但横场对三临界点的作用值得更多研究.在T-D相图中，负晶场比例较大降低有序相，正晶场比例较大增大有序相；强二模磁场和横场都抑制有序相，但强二模磁场有利于三临界点的出现，而横场抑制三临界点.在T-Ω相图中，晶场和晶场浓度对有序相范围有显著影响.

混合自旋横向Ising模型；临界行为；随机晶场；二模磁场

Jiang等人研究了晶场作用自旋为1的横向Ising模型，给出适用一般配位数的二级相变和三临界点表达式，并考察了晶场对相变的影响[1].晶场作用的横向Ising模型是横向Ising模型（TIM）和Blume-Capel模型（BCM）的发展.该模型中包含了近邻格点的交换相互作用、晶格排列引起的晶场作用，以及描述量子隧穿效应的横场作用.随后该模型受到了其他研究者的重视[2-5].Yan等人将晶场作用单自旋横向Ising模型发展为混合自旋系统[6]，一个重要结论是：补偿温度不仅受晶场控制，还受横场影响.其他研究者的工作已涉及到系统中键、晶场和横场随机性的影响，获得很多有意义的结果[7-9].最近，Li等人在不同横场作用的系统中发现过饱和磁化行为[10].总的来说，随机性的引入给系统性质带来丰富的变化.本文在有效场理论和切断近似的框架内，研究简立方晶格情形下二模磁场中随机晶场作用的混合自旋横向Ising模型的临界行为.

1 理论推导

二模磁场中随机晶场作用的混合自旋横向Ising模型的哈密顿量为：

这里的格子由子格A和子格B相互嵌套而成，子格A是自旋为1/2的磁性原子，和是z方向和x方向的自旋矩阵；子格B是自旋为1的磁性原子，和是子格B磁性原子z方向和x方向的自旋矩阵.J为最近邻格点间的交换相互作用，并设J＜0，表明所考虑系统是亚铁磁耦合，两个不同子格的磁化方向相反.若J＞0，则系统转为铁磁耦合，这里仅考虑亚铁磁耦合情况.Ω为系统横场，代表子格A和子格B的量子隧穿效应.Dj是作用在子格B上的晶场，满足随机分布

p是随机晶场浓度.当p=0时，表现为纯的负晶场；当p=1时，表现为纯的正晶场；0＜p＜1时是混合随机晶场.hα()

α=i,j是作用于系统的磁场，平行于z轴方向且满足二模分布：

在有效场理论的框架下，子格A和子格B的子格磁化σ、m具有下列形式：

子格B的四极矩q具有如下形式：

表达式中的＜…＞表示热力学平均，∇=∂/∂x是微分算符.函数F(x)、G(x)和U(x)的定义如下：

其中f(x,hi)、g(x,hj,Dj)和u(x,hj,Dj)的表达式是：

这里β=1/kBT，其它涉及量的定义为：

其中系数为：

因为涉及多自旋相关，要精确求解方程（4）-（6）相当困难，通常做法是引入切断近似，即：

有i≠j≠…≠k.在切断近似下，方程（4）-（6）可以表示为：

选取简立方格子（z=6）作为三维研究对象.联立方程（22）-（24），得到子格A磁化σ满足的自洽方程：

其中

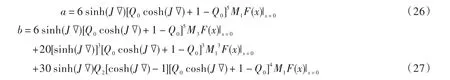
包含的系数为：

根据朗道相变理论，二级相变线附近σ很小，因此只需保留线性项，得到相变方程a=1.因为相变方程是（22）-（24）联立解的结果，其中包含子格A和B的共同贡献，因此a=1方程所得到的临界温度代表整个亚铁磁系统的临界温度.若b＜0，系统的相变为二级相变；若b＞0，系统的相变为一级相变.当一条相变线上同时存在二级相变和一级相变时，存在三临界点.而三临界点的位置由a=1和b=0所决定.

2 数值结果和分析

图1是临界温度随磁场的变化关系，分别对应于（a）D/J=1、Ω/J=0，（b）D/J=2、Ω/J=0，（c）D/J=2、Ω/J=1，不同的曲线对应不同的晶场浓度p.图1（a）表明，任意晶场浓度下，二级相变线随二模磁场的增大而单调下降，强二模磁场有效降低临界温度.相变线上均存在三临界点，但大的晶场浓度使三临界点温度升高.注意到存在一个临界二模磁场值h/J=1.84，在h/J＜1.84时，有序相的范围随二模磁场的增大而增大，这意味着此时随机晶场中正晶场的比例越大，越有利于有序相；然而h/J＞1.84时，有序相的范围随晶场浓度的增大而减小.即二模磁场分布条件下，随机晶场浓度的大小对有序相的影响需要分段考虑.从图1（b）中看到，晶场增大对三临界点有显著影响.在0≤p≤0.38范围内，三临界点被完全抑制.在0.39≤p≤0.49范围内，在二级相变线中出现部分一级相变过程，即在一条相变线上存在双三临界点，在此范围内随着晶场浓度增大，两个三临界点分别向高温和低温方向发展.在p≥0.5时，低温的三临界点消失，高温的三临界点随晶场浓度的增加继续升高.因此在晶场值增大后，较大的负晶场比例（p较小）能有效抑制三临界点；适当大小的随机晶场浓度能导致双三临界点的出现.与图1（a）相比，零场时的居里温度分别向高温与低温方向扩展，由于p=0为纯负晶场，大的负晶场使得零场时的有序范围减小，p=1时则反之.在0≤p≤0.05内有序相的范围扩展到更大的磁场处.另一方面在0.06≤p≤0.46内，观察到二级重入相变现象，且随着晶场浓度的增加重入现象逐渐抑制直至消失.因此二级重入相变现象与大的晶场和适当的随机浓度有关.注意到基态时二级相变线在0≤p≤0.05和0.06≤p≤0.38分别聚于横轴的两点，说明基态时在一定的晶场浓度范围内出现简并态，在相图上即表现为相变线交于同一点.图1（c）中，在0≤p≤0.32范围内观察不到三临界点，与图1（b）比较晶场浓度范围有所减小.以往的工作普遍认为横场能有效抑制三临界点，而这里结果表明，在T-h空间中横场对三临界点的影响不同，因此对以往的结论需重新认识.零场的居里温度降低，二级重入相变现象消失，另外零温时二级相变线的磁场简并被打开，说明横场对这些结果有直接影响.综合图1，晶场、晶场浓度、二模磁场和横场这四个因素对居里温度、三临界点温度、二级重入相变、磁场简并等有重要作用.

图1 临界温度随磁场的变化关系（曲线上的数值是随机晶场浓度p）

图2 临界温度随晶场的变化关系（曲线上的数值是随机晶场浓度p）

图2是系统在T-D空间的相图，分别对应于（a）h/J=0.8、Ω/J=0；（b）h/J=1.6、Ω/J=0；（c）h/J=0.8、Ω/J=1，不同的曲线对应不同的随机晶场浓度p.图2（a）中，在0≤p≤0.08时存在一个三临界点，并且随着晶场浓度的增大而降低；在0.09≤p≤0.12时存在两个三临界点，它们随着晶场浓度的增大而逐渐合并；在0.13≤p≤1时，不存在三临界点.此时，增大晶场浓度抑制三临界点.当p≥pC=0.12时，相变线与横轴没有交点，这意味着无论晶场多大，低温时系统始终为有序.p=0.5时居里温度单调减小，p=0.7时居里温度先增大后减小，p=0.9时居里温度单调增大.这是因为负晶场比例较大降低有序相，正晶场比例较大则促进有序相.在图2（b）中，二模磁场的增大抑制了有序相范围.在0≤p≤0.73范围内可观察到三临界点，p=0时三临界点温度降低，然后三临界点温度随着晶场浓度的增大而升高，晶场浓度对三临界点的影响与图2（a）的结果不同.显然二模磁场的大小对三临界点有很大影响：弱二模磁场中随机晶场能抑制三临界点，强二模磁场中随机晶场则有利于三临界点.图2（c）给出了h/J=0.8、Ω/J=1时的相图，由于受到横场的影响，三临界点完全抑制，有序相范围减小.图2清晰地表明，强二模磁场和横场都抑制有序相，但强二模磁场有利于三临界点出现.

图3显示的是系统在T-Ω空间中h/J=0.8时的临界性质，分别对应于（a）D/J=1和（b）D/J=2，不同的曲线对应不同的晶场浓度p.图3（a）中，任意晶场浓度下，居里温度随着横场单调降低.随着晶场浓度增大，系统有序相的范围增加.图3（b）与图3（a）比较，居里温度分别向低温和高温方向发展，即：随机浓度小时系统有序相范围减小，随机浓度大时有序相范围增大，这也很清楚地表明负晶场抑制有序相而正晶场促进有序相.

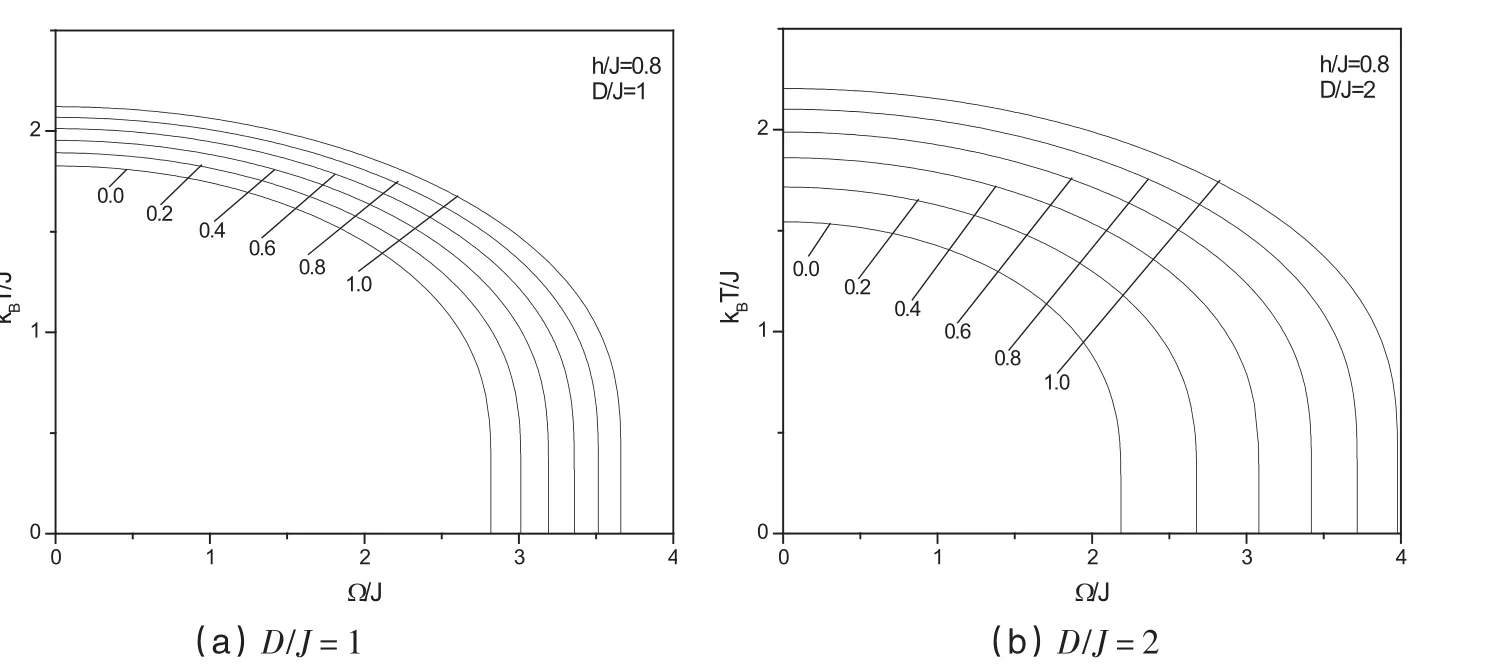
图3 临界温度随横场的变化关系（h/J=0.8，曲线上的数值是随机晶场浓度p）

3 结论

本文基于有效场理论和切断近似讨论了二模磁场中晶场作用的混合自旋横向Ising模型的临界行为.在T-h相图中，晶场浓度对有序相范围的影响需要将二模磁场分段考虑；大的晶场和适当的晶场浓度有利于二级重入相变现象；横场可打开基态的磁场简并；特别是引入横场后完全抑制三临界点的晶场浓度范围减小，表明T-h空间中横场对三临界点的影响是不同的，因此以往的结论需重新认识.在T-D相图中，负晶场比例较大降低有序相，正晶场比例较大促进有序相；强二模磁场和横场都抑制有序相，但强二模磁场有利于三临界点出现，而横场抑制三临界点.在T-Ω相图中，随着晶场浓度增大，有序相范围增加；增大晶场后晶场浓度的不同使居里温度分别向低温和高温方向发展.

[1]Jiang X F,Li J L,Zhong J L,et al.Effect of a crystal field on phase transitions in a spin-1 transverse Ising model[J].Phys Rev B, 1993,827:47-50.

[2]Jiang X F,Zhong J L,Li J L.The random-mixed-bond spin-1 Ising model with a single-ion anisotropy in a transverse field[J].J Phys:Condens Matter,1994,6:523-532.

[3]Deng L L,Yan S L.Phase transition features of the bond-dilution transverse ferromagnetic Ising spin system with random crystal field[J].J Magn Magn Mater,2002,251:138-147.

[4]Htoutou K,Ainane A,Saber M,et al.The site diluted transverse spin-1 Ising model with a longitudinal crystal-field[J].Physica A, 2005,358:184-196.

[5]Akinci U,Yuksel Y,Polat H.Effects of the bond dilution on the phase diagrams of a spin-1 transverse Ising model with crystal field interaction on a honeycomb lattice[J].Physica A,2011,390:541-552.

[6]Yan S L,Yang C Z.The compensation temperature study of the mixed Ising ferrimagnetic spin system with crystal field in a transverse field[J].Z Phys B,1997,103:93-96.

[7]Yan S L,Yang C Z.Effect of the transverse field on the bond-diluted mixed Ising spin system with single-ion anisotropy[J].Phys Rev B,1998,57:3512-3517.

[8]Benayad N,Zerhouni R,Klümper A.Mixed spin transverse Ising model with longitudinal random crystal field interactions[J].EurPhys J B,1998,5:687-695.

[9]Zhang Y N,Yan S L.Thermodynamic properties of random transverse field mixed spin system in the presence of single-ion anisotropy[J].Commun Theor Phys,2003,40:375-380.

[10]Li D R,Yan S L,Zhang Y F.Compensation behaviors and magnetization processes of different transverse fields mixed Blume–Capel model in a magnetic field[J].Sol Stat Commun,2010,150:2186-2189.

The Critical Behaviors of Mixed Spin Transverse Ising Model with the Random Crystal Field in a Bimodal Magnetic Field

DING Zhi,YAN Shi-lei
(School of Physical Science and Technology,Soochow University,Suzhou 215006,China)

Within the framework of the effective field theory(EFT)and cutting approximation,the critical behav⁃iors of mixed spin transverse Ising model with the random crystal field in a bimodal magnetic field are investigat⁃ed.InT-hspace,the effect from crystal field concentration to ordered phase range needs to be considered at different areas of bimodal magnetic field.A big crystal field and appropriate random concentration benefit the second phase reentrance phenomenon.The result shows it needs more discussion about the influence of trans⁃verse field to the tricritical point.InT-Dspace,a high proportion of negative crystal field leads to small or⁃dered phase range while high proportion of positive crystal field brings large ordered phase range.Both a big bi⁃modal magnetic field and transverse field can depress ordered phase.But a big bimodal magnetic field can in⁃crease tricritical point temperature while the transverse field suppresses tricritical point.InT-Dspace,crystal field and crystal field concentration have a marked impact on ordered phase.

critical behaviors;mixed spin transverse Ising model;random crystal field;bimodal magnetic field

O469

A

1008-2794（2013）04-0029-06

2013-05-15

江苏省高校优势学科建设工程资助项目（YK40000112）

晏世雷，教授，研究方向：凝聚态理论，E-mail：sly@szda.edu.cn.