传输线的λ/4阻抗变换特性分析
唐 涛,杜国虹,杨 玲
(成都信息工程学院电子工程学院,四川成都 610225)
传输线的λ/4阻抗变换特性分析
唐 涛,杜国虹,杨 玲
(成都信息工程学院电子工程学院,四川成都 610225)
在“微波技术与天线”课程教学中,传输线λ/4阻抗变换性是一个重要的知识点。课堂讲授中运用该特性对传输线阻抗一般做出定性结论,本文通过三种常用的传输线分析方法,对于终端负载为ZL,距离负载λ/4处的输入阻抗做了定量分析,用以直观解决这个教学难点。
微波传输线,输入阻抗,λ/4阻抗变换性
“微波技术与天线”是电磁场与微波技术本科相关专业的一门重要技术基础课。在传输线阻抗特性的教学中,有两个贯穿整个课程的重要特性:传输线上λ/4阻抗变换性和λ/2阻抗重复性。在课堂教学中,一般运用这两个特性对传输线阻抗做出定性结论,如:传输线上相隔λ/4,阻抗由容性变为感性,或者由开路变为短路等。而对一个具体的终端负载ZL,距离负载λ/4处的输入阻抗值和传输线λ/4阻抗变换性之间有什么联系,换句话说,能否使用λ/4阻抗变换性来对距离负载λ/4处的阻抗进行定量分析?
针对这个问题,本文将通过三种常用的传输线分析方法,对距负载λ/4处阻抗做出定量分析,以此作为教学上的参考。
1 输入阻抗公式法
传输线上任一点的输入阻抗Zin(z)可由输入阻抗公式求得[1]
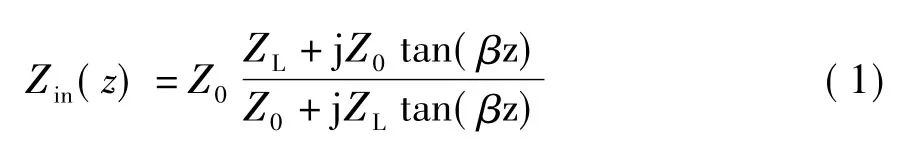
传输线上距离终端负载λ/4处的输入阻抗可根据上式求得
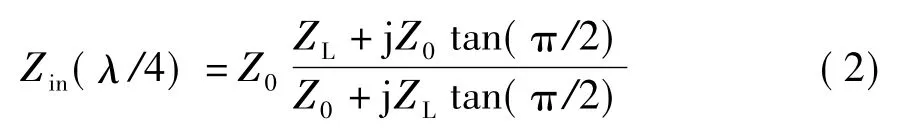
由正切函数的周期性可得Zin(λ/4)=Z20/ZL。也即是说,传输线上距离终端负载λ/4处的输入阻抗与负载阻抗存在以下关系:

由式(2)还可以进一步得出:传输线上任意相距λ/4两点间的输入阻抗的乘积等于传输线特性阻抗的平方这一结论:
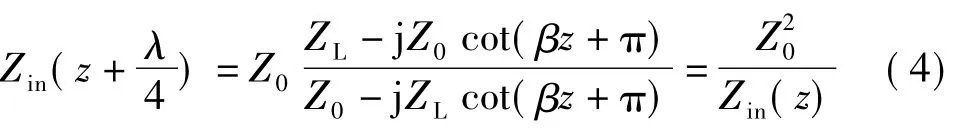
从上式还可以看出:如果传输线上z处的输入阻抗Zin(z)为0,那么与z处相距λ/4处的输入阻抗Zin(z+λ/4)为无穷大,反之,如果Zin(z)为无穷大,那么Zin(z+λ/4)为0,这就是λ/4阻抗变换性的定性解释。
2 Smith圆图法
通过Smith圆图来确定传输线的阻抗也是该课程的重点和难点。传输线上距离负载λ/4处的输入阻抗也可以由Smith圆图法来求得[2]。例如对一特性阻抗为50Ω的传输线,其负载阻抗ZL=50+j50Ω,那么距离负载λ/4处的输入阻抗可以由如下步骤确定。
(1)求归一化负载阻抗
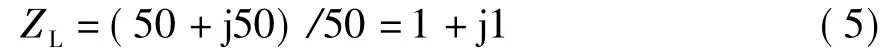
(2)在圆图上找出该点的位置,标记为A点,如图1所示。其对应的电长度为0.162。
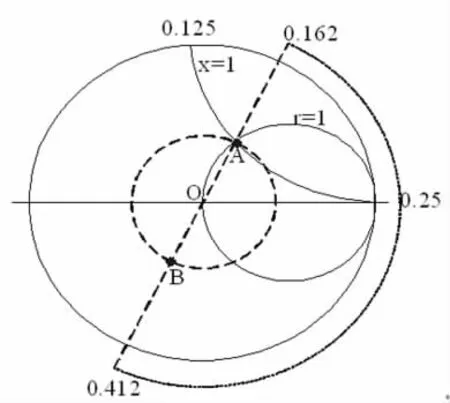
图1 Smith圆图法确定输入阻抗
因为λ/4对应的电长度为0.25,且对应圆图上的旋转角度为π,又因为已知负载在传输线上往馈源端移动,对应圆图上的顺时针旋转。
(3)作O点到A点的连线,以OA为半径画圆,即为等反射系数圆(等驻波系数圆)。沿此圆顺时针旋转0.25电长度(或者旋转角度π)至B点。
(4)读取B点的坐标为0.5-j0.5,即为该点归一化阻抗;那么距离负载λ/4处的输入阻抗为
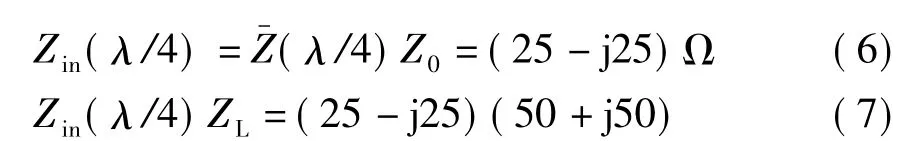
式(7)的运算结果说明该传输线特性阻抗50Ω的平方,这也印证了由输入阻抗公式(3)所得结果。
3 λ/4阻抗匹配器法
传输线的阻抗匹配,可以由戴维南等效电路来简便说明[3]。戴维南等效电路可以将一个复杂电路等效成为单一阻抗与理想电压源相串联的关系[4],如图2 所示。
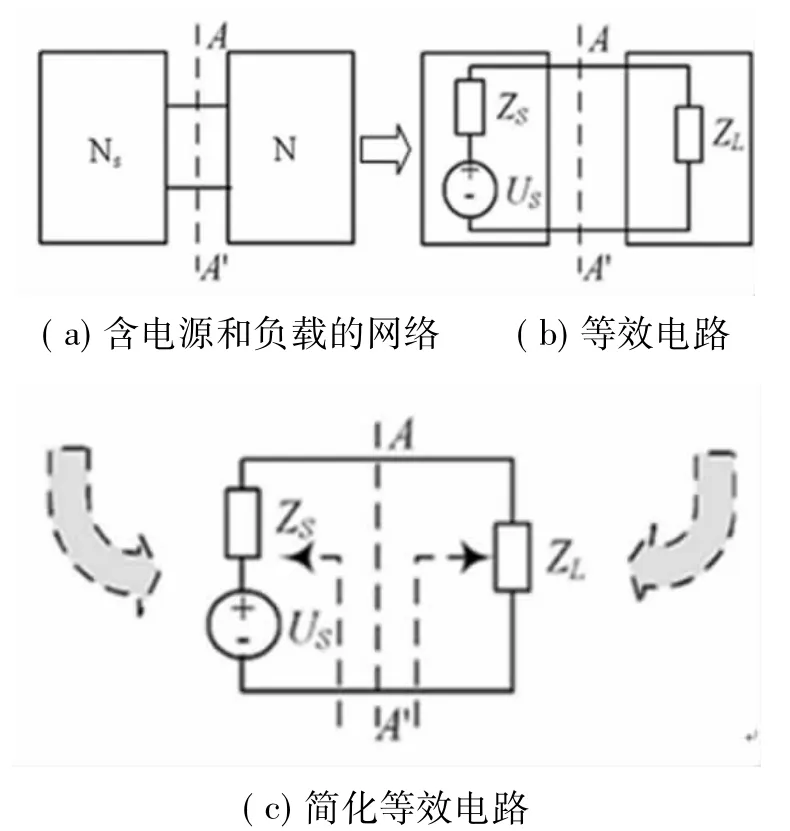
图2 戴维南等效电路简化过程
图2(a)中的NS和N分别为含有电源的阻抗网络和负载纯阻抗网络。对于所研究的(A-A’)端口的电压与电流关系由戴维南定理保证了图2(a)和图2(b)的情况完全等效,再简化可得到图2(c)。
通过戴维南定理的等效转换,研究端口的阻抗匹配问题均可简化为图2(c)来进行。信源端的阻抗ZS和负载端的阻抗ZL可以分别写成如式(8)所示的形式

常用的λ/4阻抗匹配网络,由一段长为λ/4的传输线构成,如图3所示。
当λ/4阻抗匹配网络的终端接如图3(a)所示的纯电阻负载RL时,λ/4阻抗匹配网络始端的输入阻抗为Zin=/RL,其中 Z0l为接入的λ/4传输线的特性阻抗。若λ/4阻抗匹配网络的负载不为纯电阻,而为如图3(b)所示的任意负载ZL=RL+j XL时;该段λ/4阻抗匹配网络的输入阻抗就是距离终端负载ZL为λ/4处的传输线输入阻抗。根据λ/4阻抗匹配网络始端的输入阻抗计算公式,可以直接得到Zin(λ/4)=/ZL,即为式(3)。
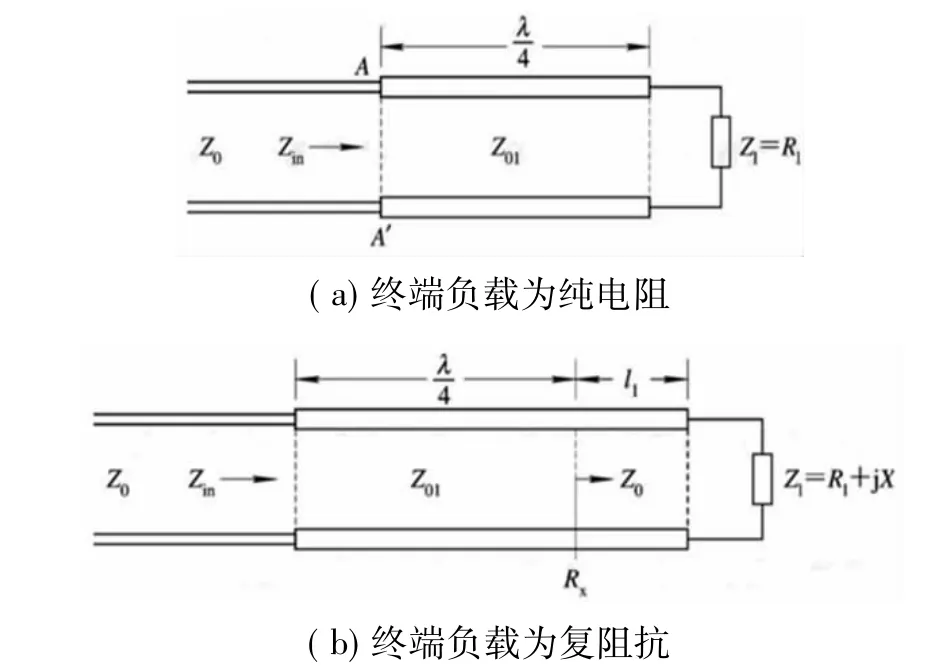
图3 λ/4阻抗匹配网络
4 结语
本文使用传输线输入阻抗的计算公式和Smith圆图以及λ/4阻抗匹配器这三种传输线阻抗分析中的重要方法,对传输线重要的阻抗特性,即λ/4阻抗变换性做了定量的分析。三种方法分别从不同角度给出了传输线上距离负载,或者相隔λ/4处的输入阻抗与负载阻抗之间的定量关系。相较λ/4阻抗变换性只能定性的解释传输线上阻抗每隔λ/4变换一次,从开路变为短路,或者从短路变成开路而言,本文得出的传输线上相距λ/4两点之间的阻抗具体值,可以由Zin(λ/4)=/ZL求得的结果更为具体。
将传输线上相距λ/2的两点输入阻抗代入式(1)可以得到Zin(z+λ/2)=Zin(z),而且,由于传输线上移动λ/2对应Smith圆图上旋转2π,所以传输线上相距λ/2处的阻抗无论从定性上还是定量上都相等,而这就是λ/2的阻抗重复性。
[1]刘学观,郭辉萍.微波技术与天线(第二版)[M].西安:西安电子科技大学出版社,2006.
[2]王新稳,李延平,李萍.微波技术与天线(第三版)[M].北京:电子工业出版社,2011.
[3]李晨晖.戴维南等效电路的求解方法及例示[J].西宁市:青海大学学报(自然科学版),2001,19(4):40-42.
[4]武岳山.阻抗匹配的种类及其在RFID系统中的应用研究[J].西安市:现代电子技术,2008,20(283):21-23.
Analysis of theλ/4 Im pedance Transformation Characteristics for Transmission Line
TANG Tao,DU Guo-hong,YANG Ling
(Electronic Engineering College,Chengdu University of Information Technology,Chengdu 610225,China)
Theλ/4 impedance transformation characteristics is a priority and a fundamental part in the teaching of the Microwave Technology and Antenna.General,a qualitative conclusion of the characteristic impedance of the transmission line is given in lectures,three common transmission line analysis methods have been employed to quantitativly analyze the λ/4 impedance for a terminal load ZLin this paper.
microwave transmission line;input impedance;λ/4 impedance transformation
TN711.1
A
1008-0686(2013)02-0019-03
2012-10-17;
2013-04-11
国家自然科学基金(61201095);成都信息工程学院科研项目与科研人才基金资助(KYTZ201211,J201202)
唐 涛(1982-),男,博士,讲师,主要从事电子科学与技术教学科研工作,E-mail:tangt@cuit.edu.cn

