缺陷板材非规则件优化排样

董德威， 颜云辉

（东北大学机械工程与自动化学院，辽宁 沈阳 110819）

缺陷板材非规则件优化排样

董德威， 颜云辉

（东北大学机械工程与自动化学院，辽宁 沈阳 110819）

针对理论上属于NPC问题的非规则件优化排样问题，论文提出一种基于小生境技术的自适应遗传模拟退火算法与基于内靠接临界多边形最低点的启发式布局算法相结合的方法。考虑到算法中交叉概率和变异概率的选择影响到算法收敛性，提出了自适应的交叉概率和变异概率，通过基于小生境技术的遗传模拟退火算法对非规则件排样的最优顺序和各自的旋转角度进行优化搜索。将非规则件定位在有缺陷原材料和非规则件多边形的内靠接临界多边形最低点以实现个体的解码，同时避开了原材料表面缺陷。排样实例表明，该优化排样算法行之有效，具有广泛的适应性。

非规则件优化排样；小生境技术；遗传模拟退火算法；启发式布局算法；临界多边形

工程实际中经常遇到优化排样问题。不规则件优化排样就是在给定的板材上将其按最优方式进行排布，要求零件排放在板材内，各个零件互不重叠且避开原材料的表面缺陷，实现最大限度地利用板材，提高效益的目的。排样问题广泛应用于机械制造、轻工、家具、皮革、服装以及印刷等行业。因此研究不规则件在板材上的优化排样具有重要的理论意义和现实意义。

排样问题实质是一个组合优化的二维布局问题，从数学复杂性理论看，是计算复杂性最高的一类 NPC问题，其计算复杂度随着排样规模的增大呈指数级增长，至今还无法找到解决该问题的有效多项式算法。Adamowicz[1]首次提出不规则件排样的启发式算法，但由于给出的只是基于某种排样顺序的准优解，因而很多学者开始尝试将人工智能算法或与启发式算法相结合来对排样问题进行研究。Liu等[2]、李明等[3]和Wang等[4]、史俊友等[5]分别应用粒子群算法和神经网络对优化排样进行了研究。Jakobs[6]提出了一种不规则件排样算法，首先求取不规则件的最小包络矩形，然后用遗传算法(Genetic Algorithm, GA)得到矩形的最优排样顺序，最后由启发式算法完成排样。因而将不规则件转变为矩形件之后进行排样成为很多学者的研究重点[7]，但此方法提高材料利用率的效果不佳。E Hopper[8]详细阐述了不规则件排样问题的研究现状，同时提出GA与临界多边形(No-Fit Polygon, NFP)算法相结合将对不规则件排样的研究起重要影响。

本文对不规则件排样的3个关键问题（排样顺序、旋转角度和定位规则）进行了研究。考虑到GA具有良好的全局搜索能力，但却存在局部寻优能力差的缺点；而模拟退火算法(Simulated Annealing Algorithm, SA)具有较强的局部搜索能力，但把握搜索过程的能力不强，因此，将二者结合作为搜索算法。同时，考虑到交叉概率过大，遗传模式被破坏的可能性大，使得具有高适应度值的个体结构很容易被破坏，交叉概率过小会使进化过程缓慢，以致停滞不前；对于变异概率，如果取值过小，则不易产生新的个体结构，如果取值过大，GA就成了纯粹的随机算法。因此，本文采用了自适应的交叉概率和变异概率[9-10]，避免了因上述情况而出现的问题。同时，利用基于预选择机制的小生境技术对子辈个体是否替换父辈个体加以控制。本文将基于小生境技术的自适应遗传模拟退火算法(Adaptive Genetic Simulated Annealing Algorithm Based on Niched Technology, ANGSA)作为搜索算法来得到不规则件的最优排样顺序和各自旋转角度。对于零件的定位规则，用于矩形件排样定位的BL算法、下台阶算法或者最低水平线算法并不能用于不规则件的定位。因而，提出了将不规则件定位在有缺陷板材和不规则件多边形的内靠接 NFP最低点的方法。此方法不但实现了不规则件的定位，而且避开了原材料表面缺陷，还避免了应用最小包络矩形定位所造成的材料利用率不高的问题。

1 不规则件排样问题数学模型

1.1 问题描述

不规则件的优化排样问题是在若干张形状不规则且有表面缺陷的板材内，将若干不规则件P1，P2，…Pn按最优方式进行排样，排样的目的是使得板材的利用率最高，在排样过程中，不规则件的需求数量未必是 1，所以 Pi和 Pj(i≠j; i,j=1,2,…, n)可能是尺寸相同的不规则件。排样过程要求满足以下约束条件：

1） Pi, Pj(i≠j；i, j=1,2,…, n)互不重叠；

2） Pi(i=1,2,…, n)与板材表面缺陷不重叠；

3） Pi(i=1,2,…, n)必须放置在板材内部；

4） 满足一定的工艺要求。

1.2 排样数学模型

不规则件、不规则板材以及板材表面缺陷的形状可以分别用以字母P、M和D所代表的多边形来表示。多边形定义为N个按逆时针方向排列的多边形顶点的有序集合{(x1, y1), (x2, y2), …(xi, yi),…,(xN, yN)}。取板材的最小x坐标和最小y坐标所确定的点作为坐标原点，由此便可确定M以及D的各顶点坐标。

不规则件Pi在板材上的定位需要4个参数(xi,yi,θi,fi)来确定。其中：(xi, yi)表示 Pi的参考点坐标；θi表示Pi的旋转角度，θi∈ [0°, 360°)；fi为 Pi关于 x=xi轴的镜像标志：fi= 0表示取 Pi本身进行排样，fi=1表示取Pi关于x=xi轴的镜像进行排样。由这4个参数便可确定排样后Pi的各顶点坐标。不规则件本身及其镜像如图1所示。

图1 不规则件本身及其镜像

设 Spi为 Pi(1≤i≤n)的面积，H为所有不规则件排样后在板材上所达到的最大高度，H线以下（包括与H线相交）共有m个表面缺陷Dj(1≤j ≤m)，Sdj为Dj的面积（与H线相交的表面缺陷，取H线以下部分的面积），S为H线以下板材总面积，因所有不规则件未必能在一张板材内排下，若需要k张板材Ml(1≤l≤k)，则用Sml来表示Ml的面积。板材的利用率F定义为所有不规则件的面积和与 H线以下无缺陷的板材面积之比，同时考虑约束条件，不规则件的优化排样问题的数学模型可表述为：

其中：第一个约束保证任意两个不规则件不重叠；第二个约束保证不规则件与表面缺陷不重叠；第三个约束保证不规则件排样在板材内部。

2 不规则件排样顺序及各自旋转角度

本文由ANGSA来得到不规则件的排样顺序及各自旋转角度，下面对算法的一些关键技术进行说明。

2.1 个体编码

不规则件的优化排样采用十进制编码。将n个不规则件P1, P2, …Pn分别用整数l, 2, …, n进行编号，不规则件编号构成一个排列{x1, x2,…, xi,…, xn}，xi是排样顺序为i的不规则件编号，为排列中的每个编号增加一个角度θi和镜像标志fi，便可得到个体的编码X={( x1,1θ, f1), ( x2,2θ, f2),…, ( xi,iθ, fi),…, ( xn,nθ, fn)}。考虑到排样时间的限制，限定不规则件旋转角度只能为某个角度基数θg的整数倍。有研究表明，不规则件旋转角度基数θg≤7°时，材料利用率的变化很小，因此，本文取θg≤9°，即在360°范围内，每个不规则件有40个旋转角度。

2.2 适应度函数

对个体的好坏用适应度函数评价，适应度函数值越大，个体质量越好。对于优化排样问题，适应度函数应是衡量排样结果优劣的一个标准，因此，本文的适应度函数用板材的利用率用F来表示。即对于个体Xi（1≤i≤M，M为群体规模），其适应度函数值为F(Xi)。

2.3 遗传算子

2.3.1 选择算子

为避免父辈群体产生的最佳个体丢失，同时使适应度函数值较高的个体有更多的生存机会，采用最优保存策略与“轮盘赌”选择法相结合的选择算子，将父辈群体中适应度函数值最大的个体直接选择到下一代，其余的 M-1个个体采用“轮盘赌”选择法进行选择。

2.3.2 交叉算子

交叉是产生新个体的主要方法。本文采用双点交叉，首先将父辈群体中的M个个体进行两两随机配对，得到M′对个体，M′为M/2的下取整。对一对个体中的两个个体X1，X2执行交叉操作之前，先在[0,1]之间生成一个随机数rc，如果rc大于交叉概率Pc，则对这对个体执行交叉操作，产生两个新个体 X1new，X2new，否则不执行。双点交叉是在1～n的范围内随机产生两个交叉位b1，b2(1≤b1＜b2≤n)，将X1中位于b1和b2之间的基因复制作为X1new前面的基因，剩余基因按在X2中出现的顺序复制到 X1new的后面，同样的方法可以得到另一个子辈个体X2new。

假设配对的两个个体为：

2.3.3 变异算子

变异是产生新个体的辅助方法。针对个体编码的形式，本文对父辈群体中任意一个个体X分别采用顺序变异和角度及镜像标志变异两种变异方式。对个体X执行变异操作之前，先在[0,1]之间生成一个随机数 rm，如果 rm大于变异概率Pm，则对这个个体执行变异操作，否则不执行。

顺序变异就是随机生成两个1～n的范围内的顺序变异位c1，c2(1≤c1＜c2≤n)，将个体X中的第c1个基因和第c2个基因的位置互换。

假设执行顺序变异操作的个体为：

X ={(4, 252°, 1), (6, 81°, 0), (1, 153°, 0), (3, 306°, 1), (5, 18°, 0), (2, 207°, 1)}

顺序变异位c1=2，c2=4，则执行顺序变异之后得到的新个体为：

X′={(4, 252°, 1), (3, 306°, 1), (1, 153°, 0), (6, 81°, 0), (5, 18°, 0), (2, 207°, 1)}

角度及镜像标志变异就是随机生成一个1～n范围内的角度及镜像标志变异位d，将执行顺序变异之后得到的新个体X的第d个基因的角度及镜像标志分别用各自的等位数值来代替，得到执行变异之后的新个体Xnew。

2.4 基于预选择机制的小生境技术

为了有效地保持群体的多样性以及考虑到子辈个体与父辈个体之间的相似性，本文对于交叉操作和变异操作之后得到的子辈个体是否替换父辈个体采用了基于预选择机制的小生境技术[11]。

交叉运算中：

对于X1和X1new，如果F (X1new)＞F (X1)，则用X1new替换X1，否则保留X1；

对于X2和X2new，如果F(X2new)＞F(X2)，则用X2new替换X2，否则保留X2。

变异运算中：

对于X和Xnew，如果F(Xnew)＞F(X)，则用Xnew替换X，否则保留X。

2.5 遗传参数的确定

2.5.1 群体规模

群体规模 M 的大小直接影响到算法的收敛速度和求解结果，群体规模过大，算法收敛速度慢；群体规模过小，群体多样性降低，影响最终的求解结果。因此，本文采用了自适应的群体规模，群体规模随排样不规则件数量n的变化而变化，且由于个体编码中每个基因位的长度为3，则群体规模M =3n。

2.5.2 自适应的交叉概率和变异概率

在执行交叉算子和变异算子时都是通过判断所生成的随机数与交叉概率Pc和变异概率Pm的大小来决定是否执行。因为算法的性能在很大程度上受到了Pc和Pm的影响，所以，本文采用了自适应的Pc和Pm。当某个个体的适应度函数值低于群体的平均适应度函数值时，说明该个体性能较差，应取较大的交叉概率和变异概率；反之，如果其适应度函数值高于群体的平均适应度函数值，说明该个体性能优良，应取较小的交叉概率和变异概率。本文将GA中的自适应交叉概率和变异概率[12]表示如下：

其中：Fmax——群体中的最大适应度函数值；Favg——每代群体的平均适应度函数值；F′——执行交叉操作的2个个体中较大的适应度函数值；

F——执行变异操作的个体的适应度函数值；

Pc1、Pc2、Pm1和 Pm2——需事先确定，且Pc1、Pc2、Pm1和Pm2∈[0,1]。

2.6 模拟退火

对执行完GA选择、交叉和变异所得到的M个个体进行模拟退化运算，来得到新的 M个个体，并将这新生成的M个个体作为下一次迭代时GA的群体。在执行SA时，有4个问题需要作出说明：

2.6.1 初始温度

SA对初始温度要求足够高，以便满足接受概率为1的初始要求。但初始温度为无穷大是无法实现的。本文中初始温度设为：

其中：α——调节参数；

n——个体长度；

Fmax——初始群体中的最大适应度函数值；

Fmin——初始群体中的最小适应度函数值。

2.6.2 降温函数

SA中，线性降温会在高温区停留较长时间，而在低温区时，温度下降又会过快，故不能很好地完成搜索工作。比例降温弥补了这一缺陷，因此本文采用比例降温函数：

式中β为降温系数，且 β∈ (0,1)。

2.6.3 状态产生函数

状态产生函数用于在即将执行SA的个体X的邻域中产生一个新的个体Xs。结合本文中个体的编码方式，生成两个1～n的范围内的随机数s1，s2(1≤s1＜s2≤n)，状态产生函数设计为对X中位于s1到s2的基因串执行逆序操作。

假设X ={(4, 252°, 1), (6, 81°, 0), (1, 153°, 0), (3, 306°, 1), (5, 18°, 0), (2, 207°, 1)}

s1=2，s2=5，则由状态产生函数得到的新个体为：

Xs={(4, 252°, 1), (5, 18°, 0), (3, 306°, 1), (1, 153°, 0), (6, 81°, 0), (2, 207°, 1)}

2.6.4 新个体接受概率

对个体X和Xs分别计算其适用度函数值F ( X )、F ( Xs)及其差值则当 ΔF ≤ 0时，用新个体 Xs代替个体 X，当ΔF ＞ 0时，如果大于一个0到1之间的随机数，则用新个体Xs代替个体X，否则保留原个体X[13]。

2.7 算法收敛准则

在算法求解过程中，整个过程是趋于收敛的。本文设定的收敛准则为：如果两代相邻种群的平均适应度函数值之差＜0.05%，则认为算法收敛并停止迭代。否则，当遗传代数大于特定代数Genmax时，迭代自动停止，则整个迭代过程中适应度函数值最大的个体所对应的排样方案为最终排样方案。

3 不规则件排样定位规则

不规则件排样的定位规则是对个体编码的解码过程。对一个个体的编码进行解码，就是要得到该个体所对应的排样图，以便根据排样图来对个体的适应度函数值进行计算。由于临界多边形（No Fit Polygon, NFP）给出了两个多边形之间的所有可能靠接位置，因此，不规则件排样问题便转换为基于NFP的定位选优过程。

3.1 NFP定义及求解算法

NFP的定义：给定多边形A和B，固定A不动，使B在不旋转的前提下沿着A的边界运动一周，在运动过程中，B与A始终保持接触但不重叠，则B上的某个参考点在运动过程中所形成的轨迹就是B相对于A的NFPAB[14]。如果B在运动过程中在A的边界内部，则形成的NFP为内靠接NFP，否则为外靠接NFP。

NFP的求解算法众多，如移动碰撞法、凹多边形凸化分割方法、Ghosh斜率图法以及明可夫斯基矢量和法等，但由于求解算法的时间复杂度较高或者是难于处理A内部有空腔的内靠接NFP的问题，本文以基于轨迹线计算的 NFP算法[15]来对不规则件和板材的内靠接NFP进行求解。

3.2 不规则件与表面有缺陷板材的内靠接NFP

不规则件与表面有缺陷板材的内靠接 NFP可按如下步骤求得：

Step 1 求出不规则件P与板材M的内靠接NFPMP；

Step 2 求出P与M内部所有表面缺陷Dj（1≤j≤m, m为M内部表面缺陷数量）之间的外靠接NFP集合DP，DP={NFPDjP|1≤j≤m}；

Step 3 找到与NFPMP相交的NFPDjP，将其从DP集合中删除以更新DP集合，同时将相交部分从NFPMP区域减去，更新NFPMP；

Step 4 对新的 DP集合和 NFPMP重复Step3；

Step 5 直至无法找到与 NFPMP相交的NFPDjP，此时得到的 NFPMP便是不规则件与表面有缺陷板材的内靠接NFP。

NFPMP求解过程如图2所示。

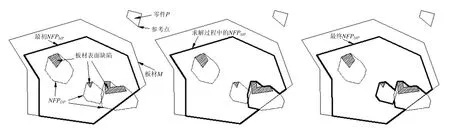
图2 NFPMP求解过程

3.3 基于内靠接NFP最低点的定位规则

由上文 NFPMP确定的不规则件位置不但保证不规则件排样在板材内部，并且避开了板材的表面缺陷。基于此提出一种将不规则件定位在有缺陷板材和不规则件多边形的内靠接 NFP最低点的定位规则。

基于内靠接 NFP最低点的不规则件在板材内部的定位规则步骤如下：

Step 1 不规则件集合SP={Pi|1≤i≤n }，板材集合 SM={Ml|1≤l≤k}，每张板材所对应的缺陷集合SDl={Dj|1≤j≤ml}，ml为第l张板材缺陷数量；

Step 2 计算第一个待排不规则件P1与第一张板材M1的内靠接NFPM1P1；

Step 3 将 P1参考点定位在NFPM1P1纵坐标最低的位置，如NFPM1P1纵坐标最低点有多个，则将P1参考点定位在最左边的那个坐标点；

Step 4 将定位之后的P1区域从M1的区域减去，此时若有表面缺陷与 P1接触，则同时将此缺陷区域从M1的区域减去，更新M1，把此缺陷从SD1中去除，把P1从SP中去除；

Step 5 计算P2与更新之后的M1的内靠接NFPM1P2，与P1类似，执行Step 3和Step 4；

Step 6 直到某个不规则件Pi，无法找到Pi与M1的内靠接NFPM1Pi，则计算Pi与M2的内靠接NFPM2Pi，与P1类似，执行Step 3和Step 4；

Step 7 直至所有不规则件排样完毕，此时SP集合为空。

4 实例分析

用两个实例验证本文所提出的不规则件排样算法的有效性和通用性。ANGSA的参数设置为：初始交叉概率Pc1为0.9，Pc2为0.6，初始变异概率Pm1为0.5，Pm2为0.1，初始温度调节参数α为5，降温函数的降温系数β为0.95，算法收敛准则中Genmax为100。

实例1 矩形板材上存在有缺陷的不规则件排样：在实际生产中，板材大多为矩形。本例中，排样板材长度 L为 1000mm，板材宽度 W为640mm，每张板材均有表面缺陷。不规则件种类数为8，每类不规则件的需求数为15。排样结果如图3所示。

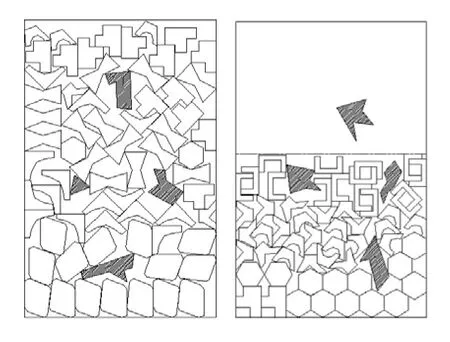
图3 不规则件在矩形板材上的排样结果图

由排样结果可知，排样共使用两张板材，图中虚线为排样结果的最高轮廓线，其高度为1554mm，板材利用率F达到了82.56%。

实例2 不规则板材上存在有缺陷的不规则件排样：不规则件与实例1相同，每类不规则件的需求数为3。排样结果如图4所示。

图4 不规则件在不规则板材上的排样结果图

5 结 束 语

针对在实际应用和理论研究方面都具有重要意义的不规则件优化排样问题，本文提出一种将ANGSA与基于内靠接NFP最低点的启发式布局算法相结合的方法。通过ANGSA来得到不规则件排样的最优顺序和各自的旋转角度，由基于内靠接 NFP最低点的定位规则实现对个体的解码。由实例可知，本文排样算法对零件形状和板材形状均无要求，同时允许板材表面缺陷的存在，具有较强的有效性和通用性。在大批量生产时，本文提出的算法提高了板材的利用率，具有显著的经济效益和重要的现实意义。

[1] Adamowicz M. The optimal two dimensional allocation of irregular, multiple connected shapes with linear, logical and geometric constrains [D]. New York:New York University, 1969.

[2] Liu D S, Tan K C, Huang S Y, et al. On solving multiobjective bin packing problems using evolutionary particle swarm optimization [J]. European Journal of Operational Research, 2008, 190(2):357-382.

[3] 李 明, 宋成芳, 周泽魁. 二维不规则零件排样问题的粒子群算法求解[J]. 江南大学学报(自然科学版), 2005, 4(3):266-269.

[4] Wang Chunxi, Cao Yuedong, Zha Jianzhong. Neural algorithms of two dimensional packing [C]// Proceeding of the 3rd World Congress on Intelligent Control and Automation. Hefei, China, 2000:1127-1131.

[5] 史俊友, 苏传生, 瞿红岩. 不规则零件优化排样的神经网络混合优化算法[J]. 工程设计学报, 2009, 16(4):271-275.

[6] Jakobs S. On genetic algorithms for the packing of polygon [J]. European Journal of Operational Research, 1996, 88(1):165-181.

[7] 贾志欣, 殷国富, 罗 阳. 二维不规则零件排样问题的遗传算法求解[J]. 计算机辅助设计与图形学学报, 2002, 14(5):467-470.

[8] Hopper E, Turton H. A review of the application of meta-heuristic algorithms to 2D regular and irregular strip packing problems [J]. Artificial Intelligence Review, 2001, 16:257-300.

[9] Bekiroglu S, Debe T, Ayvaz Y. Implementation of different encoding types on structural optimization based on adaptive genetic algorithm [J]. Finite Elements in Analysis and Desigh, 2009, 45(11):826-835.

[10] Lee Chienpang, Lin Wenshin, Chen Yuhmin, et al. Gene selection and sample classification on microarray data based on adaptive genetic algorithm/k-nearest neighbor method [J]. Expert Systems with Applications, 2011, 38(5):4661-4667.

[11] 周 明, 孙树栋. 遗传算法原理及应用[M]. 北京:国防工业出版社, 1999:74-78.

[12] 王小平, 曹立明. 遗传算法——理论、应用与软件实现[M]. 西安:西安交通大学出版社, 2001:73-74.

[13] Suman B. Study of simulated annealing based algorithm for multi objective optimization of a constrained problem [J]. Computer & Chemical Engineering, 2004, 28(9):1849-1871.

[14] Burke E K, Hellier R S R, Kendall G, et al. Complete and robust no-fit polygon generation for the irregular stock cutting problem [J]. European Journal of Operational Research, 2007, 179(1):27-49.

[15] 刘胡瑶, 何援军. 基于轨迹计算的临界多边形求解算法[J].计算机辅助设计与图形学学报, 2006, 18(8):1123-1129.

Optimal Packing of Irregular Parts on Plates with Defects

Dong Dewei, Yan Yunhui
( School of Mechanical Engineering & Automation, Northeastern University, Liaoning Shenyang 110819, China )

Aiming at the optimal packing problem of irregular parts, known as a NP-complete problem, an approach is presented, which combines adaptive niche genetic simulated annealing algorithm with a heuristic packing algorithm based on the lowest point of inside no fit polygon. Considering that the choice of crossover probability and mutation probability will affect algorithm convergence, the adaptive crossover probability and the adaptive mutation probability are putted forward. The proposed approach automatically looks for the best sequence of the irregular parts and each part’s optimum rotation angle by the genetic simulated annealing algorithm which is based on the niche technology. The lowest point of inside no fit polygon, which is created by the damaged raw material polygon and the irregular part polygon, is selected to locate the part. Meanwhile, the overlap of the part and the surface defect of raw material are avoided. Examples indicate that the approach is effective and practical.

optimal packing of irregular parts; niche technology; genetic simulated annealing algorithm; heuristic packing algorithm; no fit polygon

TP 391.7

A

2095-302X (2013)02-0031-07

2012-05-03；定稿日期：2012-06-27

国家自然科学基金资助项目(50574019)；国家高技术研究发展计划(863计划)资助项目(2008AA04Z135)；中央高校基本科研业务费专项资金资助项目(N100603002)

董德威（1983-），男，辽宁朝阳人，博士研究生，主要研究方向为图像处理、计算机辅助设计。E-mail：weidragon007@sina.com

颜云辉（1960-），男，江苏丹阳人，教授，主要研究方向为图像处理与计算机应用技术，虚拟设计与仿真技术。E-mail：yanyh@mail.neu.edu.cn