多焦点圆及其椭圆和卵圆

管贤根， 管 杰

（1. 巢湖市农委，安徽 巢湖 238000；2. 北京邦天信息技术有限公司，北京 100086）

家禽的卵（蛋）是人们喜爱的食物，它的纵截面形状，习惯上称为卵圆。尽管人们对卵圆的直观认识由来已久，至今未能对卵圆有一个明确的描述和定义，对圆形的认识，仍然停留在圆[1]和椭圆[2]阶段。

圆是一个焦点，称做圆心，椭圆是两个焦点。从焦点数目和图形的角度分析，增加一个焦点，使圆变扁形成了椭圆。卵圆与椭圆类似，若能通过增加焦点数目使椭圆变形，完全有可能得到卵圆。由此联想提出多焦点圆概念，应用多焦点圆的原理和方法，探讨对椭圆和卵圆的图形特征与性质的基本认识。为图形设计和相关学科研究提供新的方法。

1 多焦点圆概念

与圆和椭圆的焦点数目相比较，多焦点圆是泛指两个及其以上焦点数目圆的总称，是圆和椭圆概念的扩展。相同参数不同焦点数和焦点形状多焦点圆的图形特征，见图1。

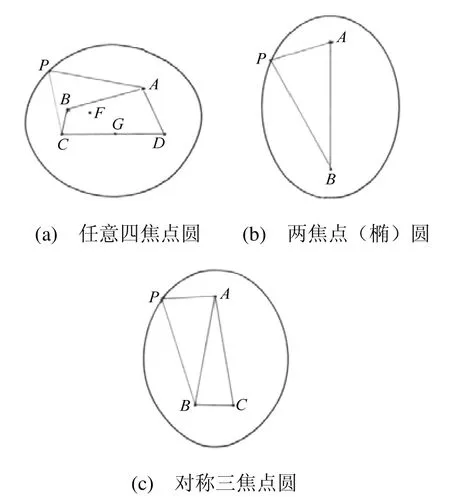
图1 多焦点圆示意图

1.1 多焦点圆定义

为便于对多焦点圆、椭圆和圆的统一描述，引用相关术语。

1） 定点：平面内的已知点或固定点。

2） 焦点环线：环绕定点一周最短的环形线，用L0表示。

3） 焦点多边形：焦点环线形成的几何图形。

4） 焦点：焦点多边形顶点的定点。

5） 环线：动点与焦点多边形所形成的环形线，用L表示。

有了图1和术语，可以对多焦点圆作初步的描述，把多焦点圆看作是以焦点多边形为“圆心”，环线为“半径”的“圆”。

多焦点圆定义：平面内，与n个定点间形成的环线长为常数的点的轨迹称做多焦点圆。定点间的环线形状称做焦点多边形，顶点称做焦点，焦点多边形是多焦点圆的基本属性。

1.2 多焦点圆的特征特性

1.2.1 环线比值(k)

环线长和焦点环线长的比值k为无单位量，是多焦点圆的形状特征和属性的参数。表达式为：

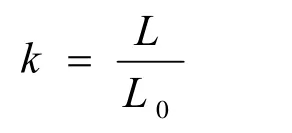
环线比值(k)在对称多焦点圆的图形与参数和特征参数分析中，起到重要作用。

1.2.2 多焦点圆的曲线

圆周曲线是由环线和焦点所确定的多条不同的椭圆曲线，通过相切连接形成的凸闭合光滑曲线。选择适合的坐标系，各段椭圆曲线根据参数均可建立对应的椭圆方程，能够对图形作具体分析。

1.2.3 多焦点圆的图形

多焦点圆是有规则的凸闭合曲线图形。环线、焦点数目和形状是多焦点圆的基本参数，确定多焦点圆的图形特征如：图形的大、小；形状的长、扁和对称性等。焦点多边形具有形和量的变化特征，参数的任何一项变化，都会引起图形的相应变化，属于多参数图形。

1.3 多焦点圆的类型

尽管多焦点圆有多种不同的形状，根据图形特征，分为对称和非对称两类。

1.3.1 对称多焦点圆

焦点多边形为对称几何图形的多焦点圆称为对称多焦点圆。对称多焦点圆具有对称轴，根据对称轴数目进一步分为3种类型：

1） 一条对称轴多焦点圆——卵形曲线

焦点多边形为等腰三角形、纺锤形（一条对角线为对称轴，对称边相等的四边形）、等腰梯形和其他具有一条对称轴图形的多焦点圆，图形类似家禽和鸟类卵的形状，称为卵形曲线。规范标准的卵形曲线称为普通卵圆；具有形成图形内在规律的卵圆称为标准卵圆。根据焦点形状和数目命名。

2） 两条对称轴多焦点圆——椭圆形曲线

焦点多边形为线形、棱形、长方形、六边形等具有两条对称轴图形的多焦点圆称为椭圆形曲线。规范标准的椭圆形曲线称为普通椭圆，具有形成图形内在规律的椭圆称为标准椭圆，根据焦点形状和数目命名。

3） 三条及其以上对称轴多焦点圆——多轴圆

焦点为正多边形的多焦点圆有多条对称轴，对称轴数与焦点正多边形的边数相同；重心在中点，类似于圆的圆心，属于规范标准曲线图形，故称为多轴圆，根据正多边形命名。

1.3.2 非对称多焦点圆

焦点多边形为非对称几何图形的多焦点圆，称为非对称多焦点圆。如焦点为任意三角形、任意四边形以及其他没有对称轴多边形的多焦点圆。非对称性多焦点圆图形复杂，没有确定的外部特征，大部分多焦点圆属于这一类。

对称多焦点圆具有独特的外部特征——长、宽和半轴（宽与对称轴交点将对称轴分为上、下不相等的半轴，长的半轴简称为半轴下同），外部特征值称为特征参数。为了方便叙述，把对称多焦点圆简称为多焦点圆（下同）。

1.4 多焦点圆作图

根据多焦点圆定义，介绍一种简易的针线作图方法：（1）自制能缩、放的环形线、大头针、直尺和笔。（2）在作图平面上作出已知点或多边形。（3）将大头针分别直立、固定在已知点或多边形的顶点上；（4）将符合长度的环形线套在大头针外，画笔由内向外拉直环线移动一周。

针线作图属于连续移动的基本作图方法，适合圆和椭圆的作图和施工放样，作图软件有待开发。

1.5 分析方法

多焦点圆的环线（L）和焦点多边形的参数称为参数；反映图形特征的长、宽和半轴称为特征参数。可以从参数和特征参数两方面，分析多焦点圆的图形特征。

1.5.1 参数分析

根据已知参数值，建立参数与特征参数关系式，对多焦点圆作以下 5个方面分析：（1） 计算对称多焦点圆的特征参数（长、宽、和半轴）。（2） 计算周长（近似值）、面积。（3） 建立各弧段的椭圆方程。（4） 多焦点圆作图（只有参数方可作图）。（5） 多焦点圆的图形设计。

1.5.2 特征参数分析

根据对称多焦点圆的特征参数求解参数，再由所求的参数对多焦点圆作参数分析。由于多焦点圆的参数与特征参数关系的复杂性，难以直接解出参数值。通过建立多焦点圆的参数与特征参数关系式，采用参数模拟计算方法，能够对4个焦点以内的对称多焦点圆的参数求解。

不同环线长、焦点数和焦点多边形的多焦点圆，表现出独特的图形特征。椭圆、卵圆和多轴圆属于不同对称轴数的对称多焦点圆，对于人们认识自然和国民经济建设具有重要意义。应用多焦点圆的原理和方法进行分析，使我们对各种对称多焦点圆，有一个基本认识。

2 椭 圆

椭圆的图形特征是：具有两条对称轴，两个特征参数（长和宽），规范标准的闭合曲线。具有形成规律的椭圆称为标准椭圆。根据对具有两条对称轴的多焦点圆图形分析，线形两焦点和棱形四焦点椭圆是两种类型的标准椭圆，见图2。

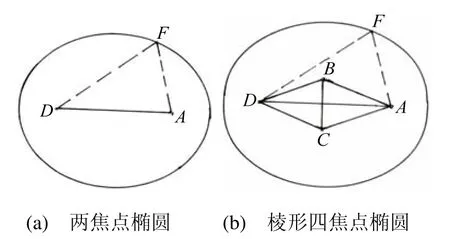
图2 标准椭圆示意图

2.1 两焦点椭圆

两焦点椭圆是由圆锥曲线理论确立的内在规律，定义是：平面内，与两个定点间的距离和为常数（常数大于两个定点间的距离）的点的轨迹为椭圆。两个定点叫做焦点，焦点间的距离叫做焦距。

以多焦点圆方法两焦点椭圆的定义是：平面内，与已知(AD)线段间形成的环线长为常数的点的轨迹为椭圆。线段的两个端点叫做焦点，线段是椭圆的基本属性。

两种定义的图形完全一致，只是参数不同。环线长L=FD+FA+AD=2a+2c（a：长半轴、c：焦距），焦点环线长L0=2·AD=4c。两种定义的参数关系式：多焦点圆定义中包含焦距，焦距为线段，是焦点环线的形状，是椭圆的基本参数。焦点环线为线段和多边形同样具有两种属性：（1）计量属性，线段可测量和计算，能够对椭圆进行具体分析；（2）图形属性，线段是几何图形，能够利用焦点环线的变形，衍生出各种不同的图形。标准椭圆能够根据形成原理建立参数与特征参数关系，对图形进行具体分析。

2.1.1 椭圆曲线性质

线形两焦点椭圆是规范标准的闭合曲线图形，曲线上的曲率呈现有规律的变化。不同椭圆的曲线弧段，通过相切连接形成独特的组合曲线和图形。把与椭圆曲线和图形类似，不含有收缩和扩张弧段的协调、匀称的椭圆组合曲线和图形，称为规范标准的曲线和图形。其主要特征：

1） 两条（或多条）椭圆曲线相切连接形成的组合曲线是光滑曲线，见图3。

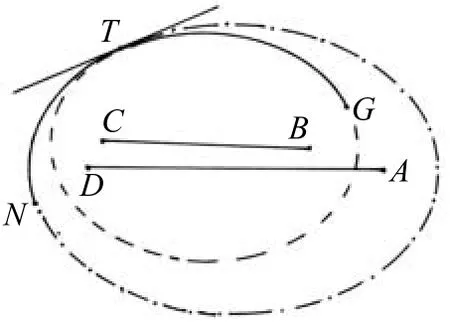
图3 椭圆组合曲线示意图

NT是以D、A为焦点的椭圆弧、TG是以C、B为焦点的椭圆弧，两个椭圆内切于T点，形成NTG组合曲线；椭圆曲线是连续可导的，切点的导数相等。因此NTG组合曲线是光滑曲线。

2） 两条对称相等的椭圆弧，对称内切于另一个椭圆形成的组合曲线，是对称、规范标准的光滑曲线，见图4。

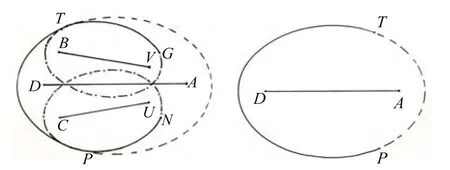
图4 椭圆组合曲线示意图

TG、PN弧段是以B、V和C、U为焦点，对称相等的两个椭圆弧，对称内切于以D、A为焦点的椭圆，切点为T、P，形成的GTPN组合曲线是对称、协调、规范标准的光滑曲线。（与右边的以D、A、为焦点椭圆的TP弧相比，图形的形状不同，但曲线的图形特征是相同的，即都是对称、规范标准光的滑曲线图形。）

3） 两个椭圆对称内切连接形成的组合曲线，是具有一条对称轴规范标准的闭合光滑曲线。图形是由两个椭圆的两条对称椭圆弧组成，且符合卵圆图形特征，故称为两段弧卵圆，见图5。

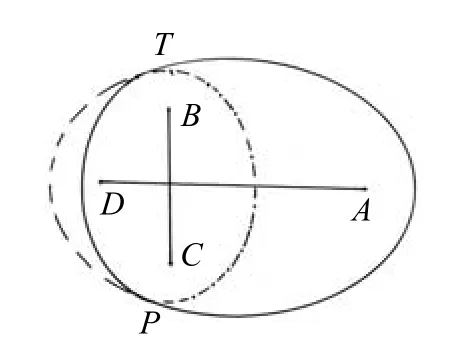
图5 椭圆组合曲线示意图

由B、C和D、A为焦点的两个椭圆，对称内切于P、T两点，形成的组合曲线是对称、协调、规范光滑曲线图形。当切点为椭圆的对称轴时，卵形曲线由两个不同椭圆的各自半条对称曲线组成，形成特定的两段弧卵圆。

4） 椭圆组合曲线2）见图4，对称内切于Y、Z为焦点的椭圆，形成具有一条对称轴的规范、标准的闭合曲线。图形是由4个椭圆的4条弧组成的卵形曲线，且符合卵圆图形特征，故称为四段弧卵圆，见图6。

以B、V和C、U为焦点的两个对称相等的椭圆，分别对称内切于Y、Z和D、A为焦点的两个椭圆，切点为G、P、M、N。形成的GPMN闭合曲线是对称、协调、规范的光滑曲线。

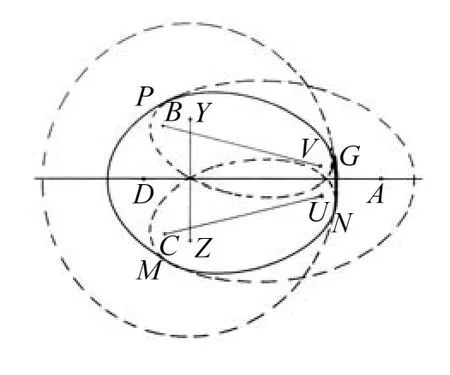
图6 椭圆组合曲线示意图

5） 在四弧段卵圆图6的PM弧段，对称内切以RQ为焦点的椭圆，形成具有一条对称轴规范标准的闭合曲线。图形是由5个椭圆的6条椭圆弧组成的卵形曲线，且符合卵圆图形特征，故称为6段弧卵圆，见图7。

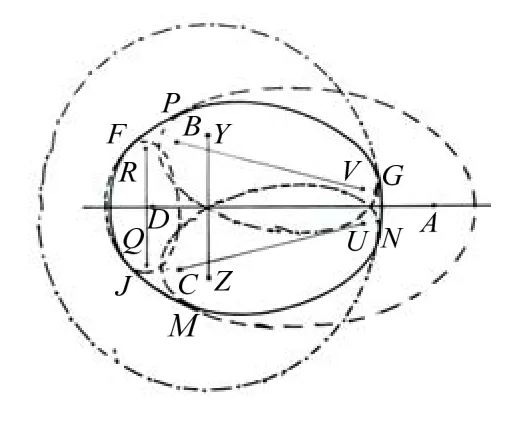
图7 椭圆组合曲线示意图

以RQ为焦点的椭圆，垂直、对称内切于四段弧卵圆的PM弧段，切点为F、J。形成的GPFJMN闭合曲线是对称、协调、规范的光滑曲线。

6） 两个相等的椭圆平行内切于另一个椭圆，形成具有两条对称轴的规范标准的闭合光滑曲线。图形有4条椭圆弧组成，且符合椭圆特征，故称为四段弧椭圆见图8。

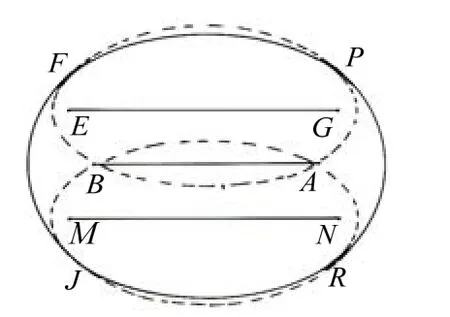
图8 椭圆组合曲线示意图

以EG和MN为焦点的两个相等椭圆，平行内切于AB为焦点的椭圆，切点为F、J、R、P。形成的FJRP组合曲线是对称、协调、规范的光滑曲线。

7） 4个相等椭圆，对称内切于两个中点重合、长轴垂直的椭圆，形成的组合曲线是具有两条对称轴的规范标准的闭合光滑曲线。图形有8条椭圆弧组成且符合椭圆特征，故称为八段弧椭圆，见图9。

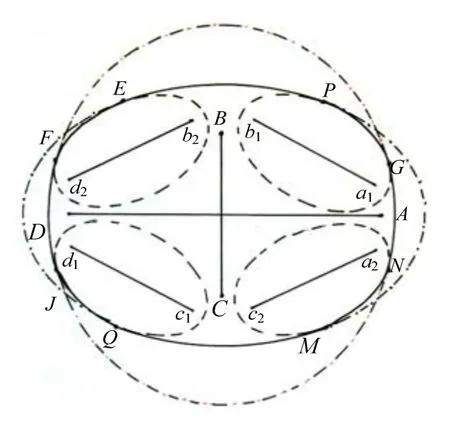
图9 椭圆组合曲线示意图

4个相等椭圆，与AD为焦点椭圆相切的切点为P、E、Q、M和与BC为焦点椭圆相切的切点为G、F、J、N。形成的GPEFJQMN组合曲线是对称、协调、规范的光滑曲线。

椭圆曲线的特性，为多焦点圆的图形分析提供依据。两段弧和四段弧卵圆为组合图形，属于普通卵圆；六段弧卵圆和八段弧椭圆具有形成图形的内在规律，由针线作图方法直接作图，属于基本图形。

2.1.2 参数与特征参数关系

1） 对称轴（长轴）

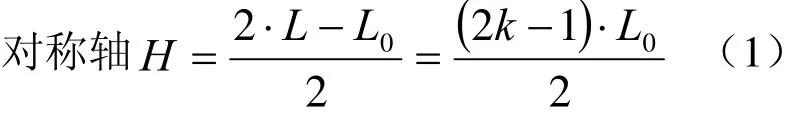
2） 宽（短轴）

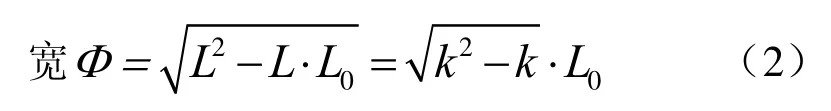
2.1.3 周长

椭圆周长没有初等函数表达式，根据椭圆积分理论，椭圆周长(C)的无穷级数计算公式[3]（或采用项名达公式以及其他近似公式，目的是寻求与参数关系。）：

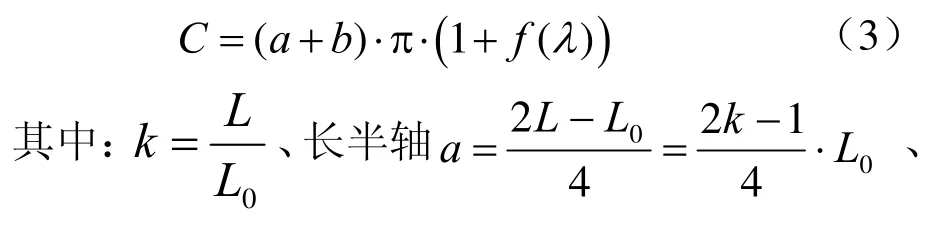
则椭圆周长的无穷级数计算公式为：

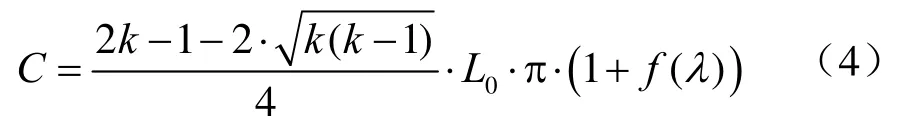
式（4）表明周长与参数k(L)、L0相关，是多焦点圆定义下两焦点椭圆周长无穷级数计算公式。

2.1.4 图形特征参数(G)

椭圆的图形特征参数是指周长与焦点环线长比值，表达式：

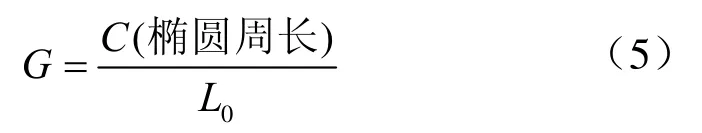
将式（4）代入式（5）得：

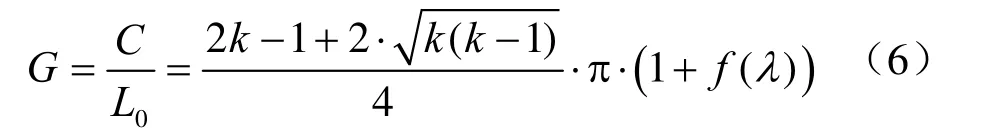
式（6）表明：G为无单位量；相同G值的椭圆是相似椭圆，其扁率、离心率相等；G与k相关也，当k为定值，G也为定值。因此，式（5）、式（6）建立了k为定值时周长与焦点环线长之间的等式关系。椭圆的这一性质，在多焦点圆的参数模拟计算中起到重要作用。

2.2 棱形四焦点椭圆

棱形四焦点椭圆是通过多焦点圆的方法获得的一种新的标准椭圆类型。定义为：与棱形焦点四边形形成的环线长为常数的点的轨迹，称做棱形四焦点椭圆。棱形是棱形四焦点椭圆的基本属性。

2.2.1 棱形四焦点椭圆曲线

根据定义作棱形四焦点椭圆曲线和各条边的延长线与圆周曲线相交示意图，见图10。显而易见棱形四焦点椭圆是由 6个椭圆的八段椭圆弧，通过对称内切连接，形成的组合曲线图形，与八段弧椭圆一致。图9中的A、a1、a23点重合为A；B、b1、b23点重合为B；C、c1、c23点重合为C；D、d1、d2重合为D，形成棱形焦点四边形ABDC。因此，棱形四焦点圆，具有椭圆基本特征，符合多焦点圆形成原理，是标准椭圆的一种新的类型。棱形四焦点椭圆属于分段函数，根据参数各段均可建立椭圆方程。（长方形和六边形的焦点多边形的椭圆曲线，不是规范标准曲线）

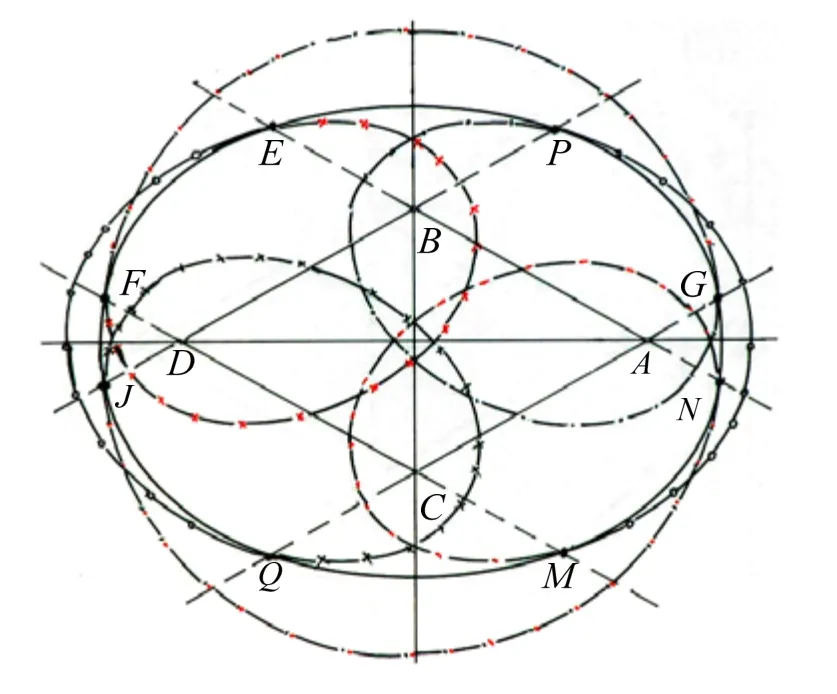
图10 棱形四焦点椭圆曲线示意图

2.2.2 棱形四焦点椭圆的参数关系

图 11为棱形四焦点椭圆示意图，已知ABDC为棱形四边形、边长设椭圆的长轴为长（H），短轴为宽（Φ），则：

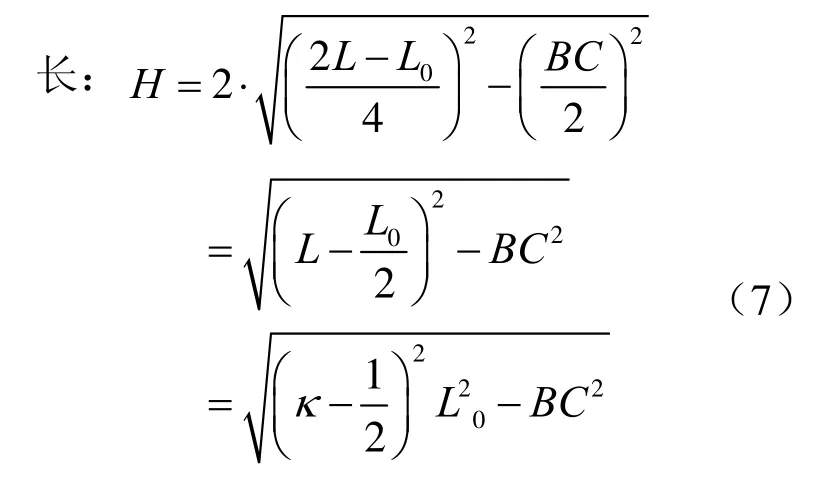
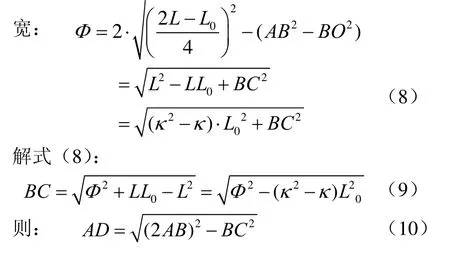
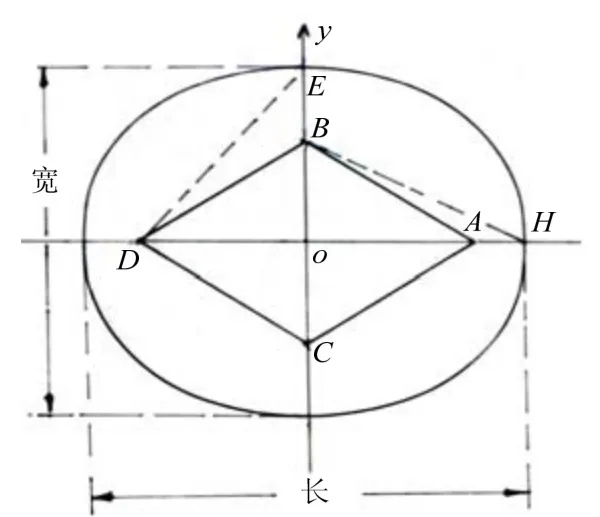
图11 棱形四焦点椭圆示意图

根据上述关系式，即可进行相关分析和参数计算。

2.2.3 棱形四焦点椭圆的图形特征

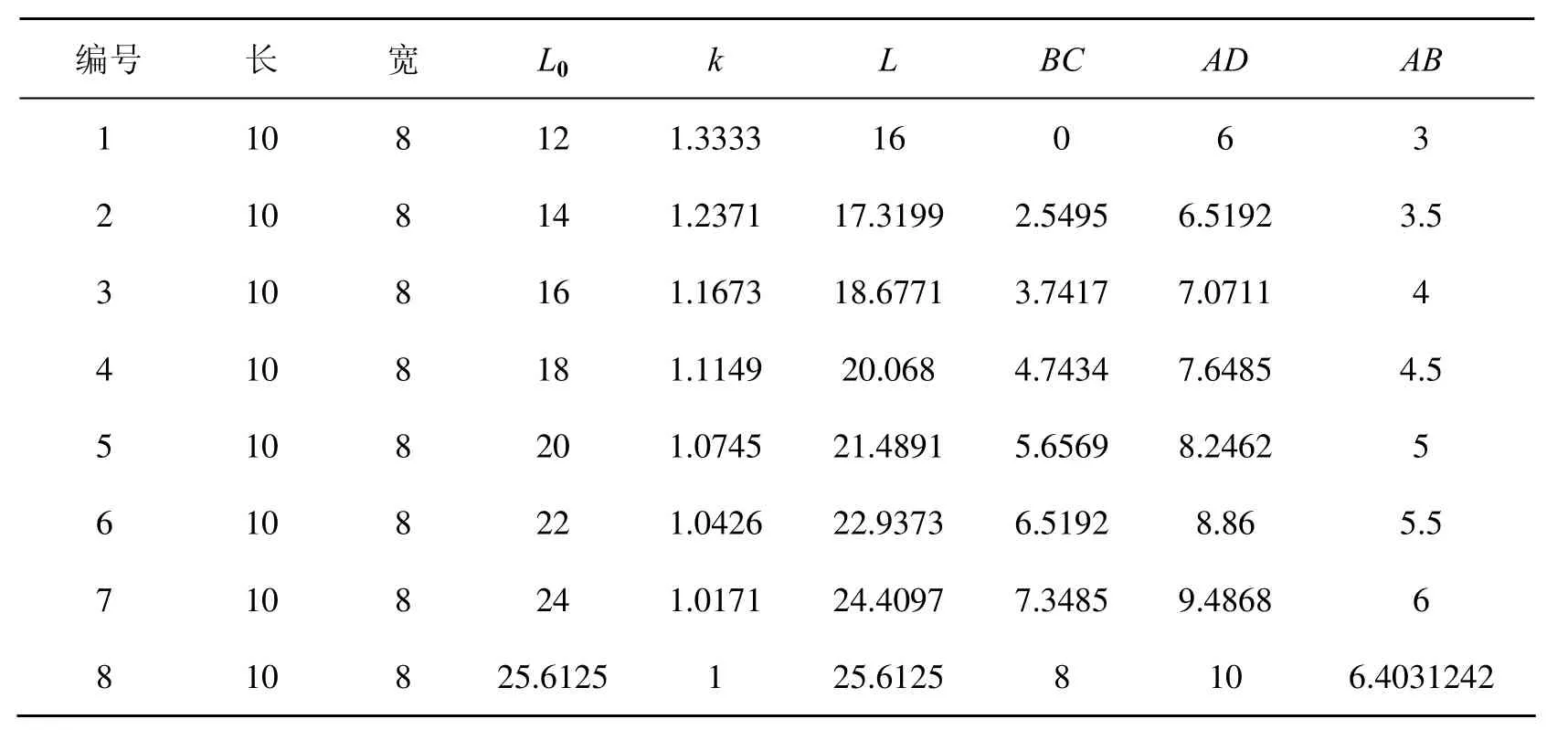
表1 相同长和宽的椭圆参数

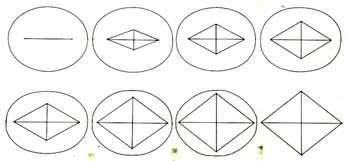
图12 相同参数不同形状棱形四焦点椭圆示意图

图12说明，棱形四焦点椭圆是长和宽相同、形状有差异的标准椭圆图形集合，是相同特征参数标准椭圆的图形库，线形两焦点椭圆是其中一员，为椭圆设计提供丰富图源。

相同特征参数椭圆的图形特征表现为，线形两焦点椭圆的焦点环线为线形，没有形状变化，因此图形是确定的；棱形四焦点椭圆的焦点图形有形状的变化，具体的图形，则需要赋予焦点形状参数的具体数值。

3 卵 圆

卵圆概念，来自于家禽、鸟类以及卵生动物的卵。整个卵（蛋）称为卵球体，纵截面形状称为卵圆。据观察，尽管各种各样的卵的形状不同，但是，卵圆都具有相同的基本图形特征：一条对称轴、三个特征参数（长、宽和半轴），规范标准的闭合曲线图形。符合卵圆基本特征的图形称为普通卵圆；具有形成内在规律的图形称为标准卵圆。

3.1 卵圆定义

一种特定条件的四焦点圆，符合卵圆的基本图形特征。即：4个焦点为纺锤形，以纺锤形边的延长线的交点为动点，与纺锤形之间形成的环线长为常数的四焦点圆。

3.1.1 特定条件纺锤形四焦点圆的图形特征

采用针线作图方法，作特定条件四焦点圆和相关辅助图见图13。焦点纺锤形各条边的延长线与卵圆周曲线相交，显而易见特定条件纺锤形四焦点圆是由5个椭圆的六段椭圆弧，通过垂直和对称内切连接，形成的组合曲线图形，与六段弧卵圆完全一致。图7中的A、V、U3点重合为A；B、R、Y3点重合为B；C、Q、Z3点重合为C；D点不变，形成纺锤形焦点四边形ABDC。因此，特定条件的纺锤形四焦点圆是具有卵圆基本特征的六段弧卵圆。（动点在交点内或交点外，形成的是8段弧卵形曲线。增加的两条曲线是对称的扩张或收缩弧段，不是规范标准的卵形曲线图形。等腰三角形和梯形焦点卵形曲线也不是规范标准的卵形曲线图形。）

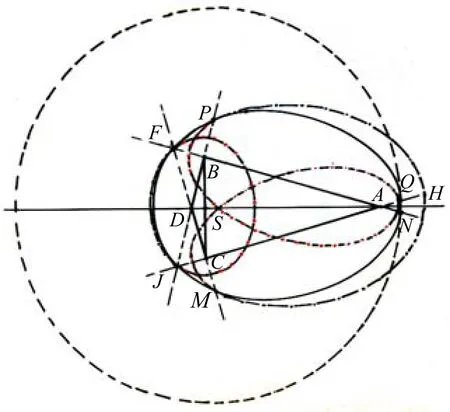
图13 四焦点圆曲线示意图

3.1.2 图形形成原理

特定条件四焦点圆是受条件约束的四焦点圆，图形的形成原理和分析方法与多焦点圆一致。

3.1.3 标准卵圆定义

由于特定条件四焦点圆符合卵圆图形特征，具有形成图形的内在规律，因此，特定条件的四焦点圆属于标准卵圆。

根据图形特征和形成规律，四焦点标准卵圆的定义：平面内，以任意纺锤形边的延长线的交点为动点，与纺锤形之间形成的环线长为常数的轨迹称做四焦点标准卵圆。纺锤形称为焦点多边形，是四焦点卵圆的基本属性。

卵圆属于多参数图形，可能有多种形成方法，有待探讨。为方便，在尚未出现新的标准卵圆时，暂将四焦点标准卵圆简称为卵圆（下同）。

3.2 曲线方程

卵圆是由5个椭圆（相关联或约束）的六段椭圆曲线通过相切组合形成的规范标准的闭合光滑曲线图形。建立适当的直角坐标系，根据卵圆参数，各段椭圆曲线都能够建立对应的椭圆方程。卵圆图形曲线属于分段函数，可以根据分段函数方程，对曲线和图形作具体分析。

3.3 参数关系

卵圆图形由纺锤形确定。对于已知卵圆的纺锤形参数，可建立关系式求出特征参数和其他参数；对于已知卵圆的特征参数，难以根据关系式求出参数，需要引进形状参数k、β，采用参数模拟计算方法方求解参数。因此，需要建立适合参数模拟计算的特征参数与纺锤形参数之间的关系式。

根据宽的极大点位置，分为三角形和椭圆形两种参数关系模式。宽的极大点位于BD延长线的内则为三角形模式；位于BD延长线的外则为椭圆形模式，见图14。两种模式分析方法类似，只是宽的计算关系式不同，限于篇幅以三角形模式为例作详细介绍。

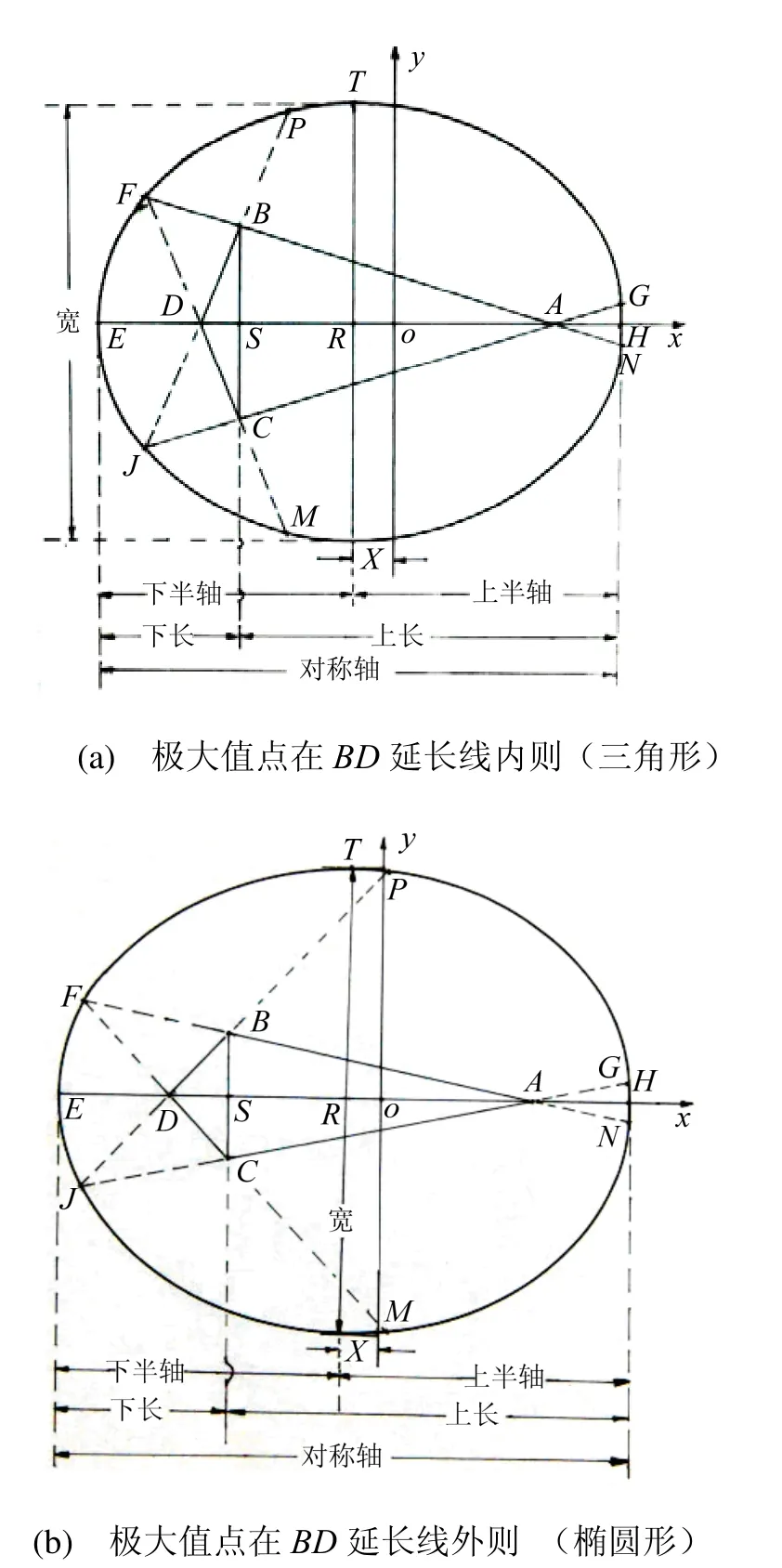
图14 卵圆参数分析示意图

设：纺锤形的长边为AB、AC，短边为BD、DC，对称轴为AD（AD=AS+DS），对角线为BC。形状参数：则：2AB=L0-β·BC。

3.3.1 宽的关系式

与对称轴垂直线段的极大值称为卵圆的宽，用Φ表示。三角形模式宽的极大点位于以A、B和A、C为焦点的两个对称椭圆弧上，由于对称性，分析一个极大点就可以了。设：T为卵圆在A、B为焦点的椭圆弧上的极大点，椭圆方程参数：

以对称轴为横轴，过AB中点为纵轴建立坐标系，通过旋转、平移得极大点对应椭圆方程：

由式（11），求得（导数或一元二次方程求极值的方法）极大点T的坐标：

3.3.2 对称轴关系式

对称轴又称为卵圆的长，用H表示。纺锤形的对角线BC，将对称轴分为两部分。（BC上长）

则对称轴：

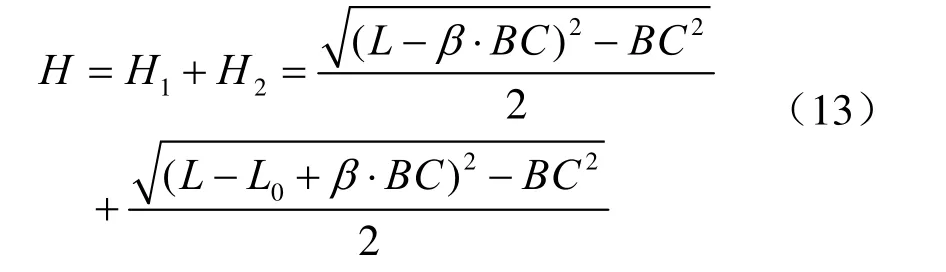
3.3.3BC关系式

BC为纺锤形的对角线，是卵圆的重要参数。解出式（12）中的BC得：

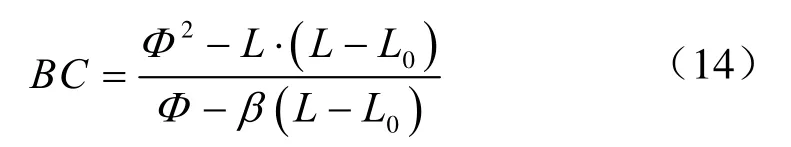
3.3.4 极大值X的关系式

X是反映宽偏离中点的参数。极大点坐标X的绝对值为：

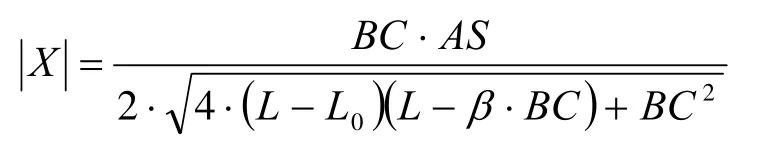
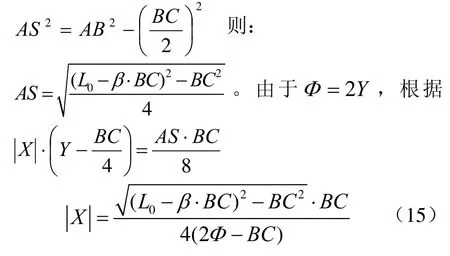
3.3.5 半轴关系式

宽与对称轴的垂足，将对称轴分为上、下两个不相等的半轴，上、下半轴的数值大小，因参数不同而相互转换，数值大的称为半轴，用R表示。

上半轴（长边）：

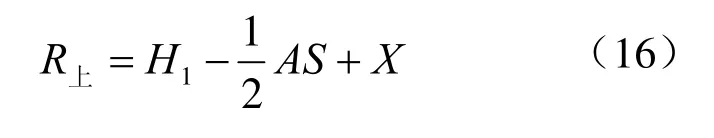
下半轴（短边）：

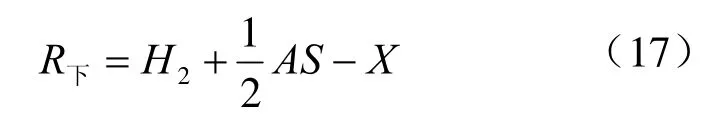
X值是应用模式的判别标准，当时，适用三角形模式；当适用椭圆形模式。建立卵圆的特征参数和参数之间的关系式，可以根据已知条件，在电脑上进行相关计算与分析。计算特征参数时，消除关系式中的形状参数计算较为方便。

3.4 焦点多边形边的延长线段的长度

焦点纺锤形的各条边的延长线与卵圆周相交参阅图14。通过建立边的线性方程，求得交点F(J)的坐标，利用交点坐标和三角计算，建立各线段长度参数关系式：

1）BD（CD）的延长线段长度：

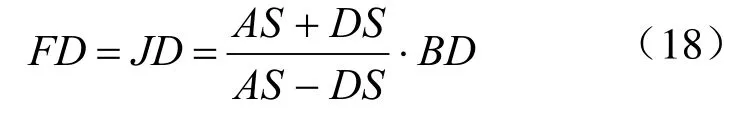
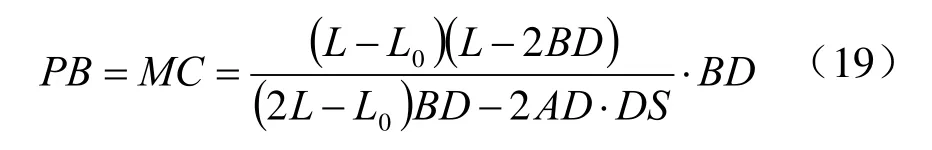
2）AB（AC）的延长线段长度：

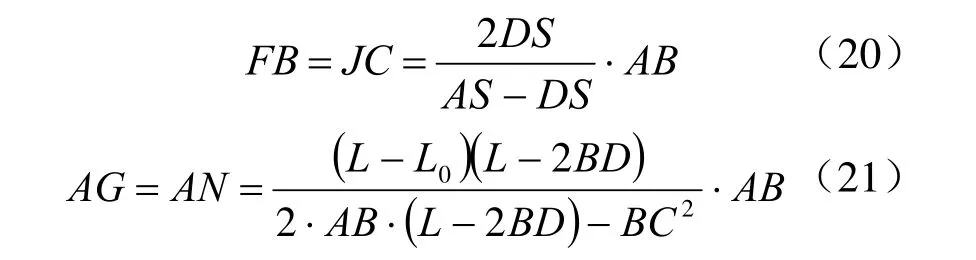
根据延长线段关系式和已知参数，即可求出各条延长线与卵圆周的交点坐标，方便对图形分析。

3.5 焦点纺锤形的特征值

纺锤形图形的参数，分为边长参数（L0、AB、BD）和对角线参数（AD、AS、DS和BC）。要确定一个纺锤形，需要含有边长和对角线三个不同的参数或参数比值。卵圆的图形特征是焦点纺锤形边的延长线交于卵圆周，由图14可知：

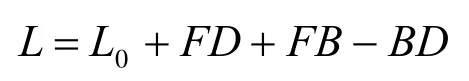
将式（18）、式（20）代入上式得：

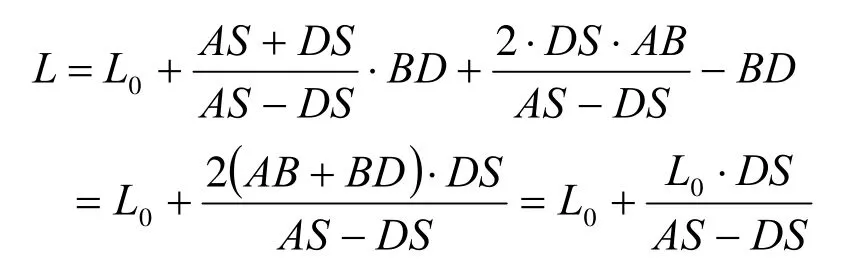
整理得：

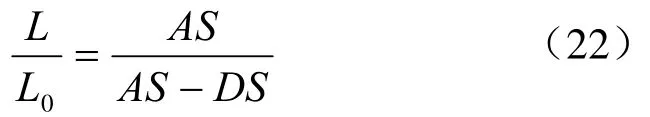
k是卵圆的形状参数，是纺锤形上、下半轴的比值，属于焦点纺锤形的形状参数。式（22）表明，卵圆的形状参数与焦点纺锤形的形状参数值相等为k。根据这一特征，任意一个纺锤形对应一个标准卵圆。

3.6 图形形状

为了解不同参数的卵圆形状，以长 12cm、宽9cm、半轴7cm的卵圆为例，以参数模拟计算方法计算出参数，作出相同长和宽不同半轴的卵圆图组和相同长和半轴不同宽的卵圆图组。使我们对卵圆图形更有直观的认识。

3.6.1 相同长和宽不同半轴的卵圆图组

卵圆的长12 cm、宽9 cm为定值，半轴分别为：6cm、6.5cm、7cm、7.5cm、8cm、8.5cm、9cm，见图15。图组特征是：半轴最小值为6cm时，对称轴的两头差异不明显，与椭圆近似相同。随着半轴长度增加，卵圆的两头差异变大，图形差异明显。

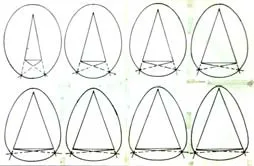
图15 相同长和宽不同半轴的卵圆图组

3.6.2 相同长和半轴不同宽的卵圆图组

卵圆长的 12cm 、半轴 7cm 为定值，宽分别为6cm、7cm、8cm、9cm、10cm、12cm、14cm、16cm，见图 16。图组特征：当宽小于长时为长型卵圆，随着宽减小卵圆变得细长；当宽大于长时为扁型卵圆，随着宽增大卵圆越扁。

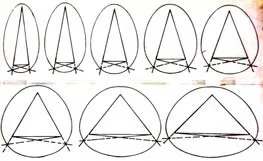
图16 相同长和半轴不同宽的卵圆图组

通过上述两组图形，可以推理出各种不同长、宽和半轴参数的标准卵圆图形特征。

4 多轴圆

多轴圆的图形特征是：焦点多边形为正多边形，对称轴和宽的数目与焦点正多边形的边数相同，对称轴和宽数目各自相等；图形由椭圆组合曲线特性予以证明，均为规范标准的组合曲线图形，不在赘述。

焦点为正三角形和正方形多轴圆的参数和特征参数分析方法与卵圆相同，焦点为正五边形及其以上的多轴圆需要结合三角函数分析，求出一条对称轴和宽即可。多轴圆的对称轴与宽的差距小，图形与圆类似，利用圆的公式以对称轴和宽的均值为直径，计算多轴圆的周长和面积，是计算卵圆周长近似值的校正系数的主要参数。

5 参数模拟计算

椭圆的参数与特征参数关系，可以相互计算。卵圆的参数与特征参数关系，只能由参数计算特征参数，而特征参数则不能直接计算出参数，这是由于两者间复杂关系决定的。采用参数模拟计算方法有效地解决计算问题。

5.1 计算原理

1） 模拟设计一个卵圆，选择一组合适的参数（k、L0和β）值，以选择的参数值和已知宽(Φ)，根据参数与特征参数关系式（宽与参数关系式较为简单），计算出模拟设计卵圆的各项参数和特征参数值。

2） 设立对称轴、半轴和纺锤形对称轴比值为对照参数，以模拟计算值与对照参数的绝对误差为比较参量。即：He（长误差）=计算H—已知H；Re（半轴误差）=计算上（下）R—已知R；ke（形状参数误差）参量值可根据精度要求设定，一般可设定三项的绝对误差＜10-4。

3） 每选择一组参数模拟值，计算出对应的参数和特征参数值与对照参数比较，得到一组对应的比较参量。经过有限次调整k、L0、β值，使得三项比较参量在允许误差内或趋向于0。

模拟计算的实质是以L0、k、β的模拟参数值和已知宽，计算出的对称轴和半轴长与已知值近似相等；形状参数与纺锤形形状参数近似相等。可以认为L0、k、β模拟参数值，就是已知长、宽和半轴三个特征参数卵圆的参数近似值。

5.2 计算步骤

5.2.1 初值确定

初值选择的合适与否直接关系到计算效果。初值取值范围是相对的，k值一般为 1.05~1.15左右；L0初值是通过间接方法确定，根据相同参数（L、L0）多焦点圆的周长近似的特性，以卵圆的近似周长C=（长+宽）÷2×3.14 ，作为相同参数椭圆周长的近似值，利用椭圆周长与焦点环线长的比值关系，以调整椭圆周长，实现对L0调整，使L0初值接近真值；β值一般为1.01~1.1左右。

5.2.2 制定计算表

表格首行列出特征参数、模拟参数（k、L0、β）和其它各项参数以及与计算和比较参量相关项。在第2行的特征参数项下，输入已知的特征参数值；在k、L0、β项下，输入各参数的初始值。其他各项是利用模拟参数初始值和宽，输入计算式（参阅前节参数、特征参数和焦点多边形关系式）得到对应值。利用公式复制功能，将第2行复制若干行，即可进行参数调整。

5.2.3k、C(L0)、β的调整

1）k值调整

k值调整只与对称轴作比较参数，比较参量是He。以L0、β初值为定值，调整k值大小，通过有限次调整，使 He在允许范围内或趋于 0。说明模拟设计卵圆的长和宽与已知卵圆的长和宽近似相等。

2）C(L0))值调整

L0值是通过调整相同参数的椭圆C（周长）而间接进行调整的。以β初值为定值，半轴为比较参数，Re为比较参量。每调整一次C(L0)值，需要重复调整k值，通过有限次调整，使得He、Re在允许范围内或趋于0，说明模拟设计卵圆的长、宽和半轴3个特征参数与已知卵圆的3个特征参数近似相等。

3）β值调整，

β值调整是使模拟设计卵圆的图形特征符合定义。以纺锤形的对称轴比值为比较参数，ke为参量值。每调整一次β值，需要重复调整k和C(L0)值，通过有限次调整，使得 He、Re、ke 3项比较参量在允许误差范围内或趋于0，说明模拟设计卵圆的长、宽和半轴3个特征参数与已知卵圆近似相等、图形符合卵圆特征。

5.3 模型选择

标准卵圆模拟参数计算模型分为三角形型和椭圆型两种，两者间的特征参数与参数关系式不同，计算方法有所不同。已知卵圆的特征参数时，首先选用三角形模型，根据计算结果，若极大值X的绝对值≥0.5DS模型选择正确，否则选用椭圆型模型。四焦点圆形成的卵圆是唯一的，根据计算的参数值，作出图形与已知卵圆的图形比较，若有明显差异，说明已知特征参数的卵圆，不属于标准卵圆。

5.4 模拟计算实例

设卵圆的3个特征参数：长=12cm、宽=8cm、半轴=7cm。试求其参数。根据卵圆的3个特征参数值，介绍在普通微机上参数模拟计算方法的详细过程，见表2。

1） 在Excel首行，例出特征参数、选择参数、参数、计算中间量和比较参量计26项。k、C(L0)、β为模拟参数，He、Re、ke为比较参量，设定误差参量值＜10-4。

2） 输入对应的特征参数值和模拟参数初值。模拟初值选择：C(L0)=（12+8）÷2×3.14=31.4、β=1.01、k=1.15。后面各项是根据参数与特征参数的关系式计算得到的对应值，且复制若干行。

3）k值调整：以β和 C(L0)初值为定值，He为比较参量。调整k时主要观察He的变化，通过有限次调整k值，当k=1.1463时，He=1.07E-05＜10-4，符合设定要求。

4） C(L0)值调整：以β初值为定值，Re为比较参量，Re有上、下半轴两个值，有一个符合设定即可。根据k值调整结果，当k=1.1463、He=1.07E-05＜10-4时，Re=-0.92049，需要调整C(L0)值，使得Re达到设定要求。每调整一次C(L0)值，需重新调整k值。如：当C(L0)为31.2时，k=1.11278、He=-1.9E-06、Re=-0.68604。继续调整 C(L0)、重复调整k。通过有限次的调整，当C(L0)=31.1718、k=1.0662时，He=-6.3E-06、Re=-7.1E-05。符合设定要求。

5）β值调整：以ke为比较参量，当He和Re两个参量符合设定要求时，通过调整β值，使得 ke达到符合设定要求。根据上一步调整结果，当 C(L0)=31.1718、k=1.0662、β=1.01时He=-6.3E-06、Re=-7.1E-05，ke=-0.034。增加β值，重新调整C(L0)和k值，使He、Re符合设定要求。再根据ke值调整β，重复调整C(L0)和k。通过有限次调整，当C(L0)=31.1552、k=1.06449、β=1.0349时，3个比较参量分别为He=1.37E-05、Re=7.34E-05、ke=2.1E-05。符合设定要求，模拟计算结束。

表格最下行是已知特征参数卵圆的各项参数和特征参数的模拟计算结果。模拟参数计算的关键是模拟参数初值的选择，若选择不当导致计算出现异常。调整过程中技巧，需要通过实例练习掌握规律。

5.5 应用实例（卵圆作图）

从市场上收集不同类型的鸡、鸭和鹅的卵（蛋），随机挑选卵（蛋）形不同的个体，用0.02mm的卡尺分别测量其长、宽和半轴3个特征参数。选用卵圆的三角形模式，根据测量数据，进行参数模拟计算，求得相关参数，见表3。根据模拟计算得出各个体卵（蛋）的参数，采用针线作图方法，进行手工作图并与实体比较，见图17。

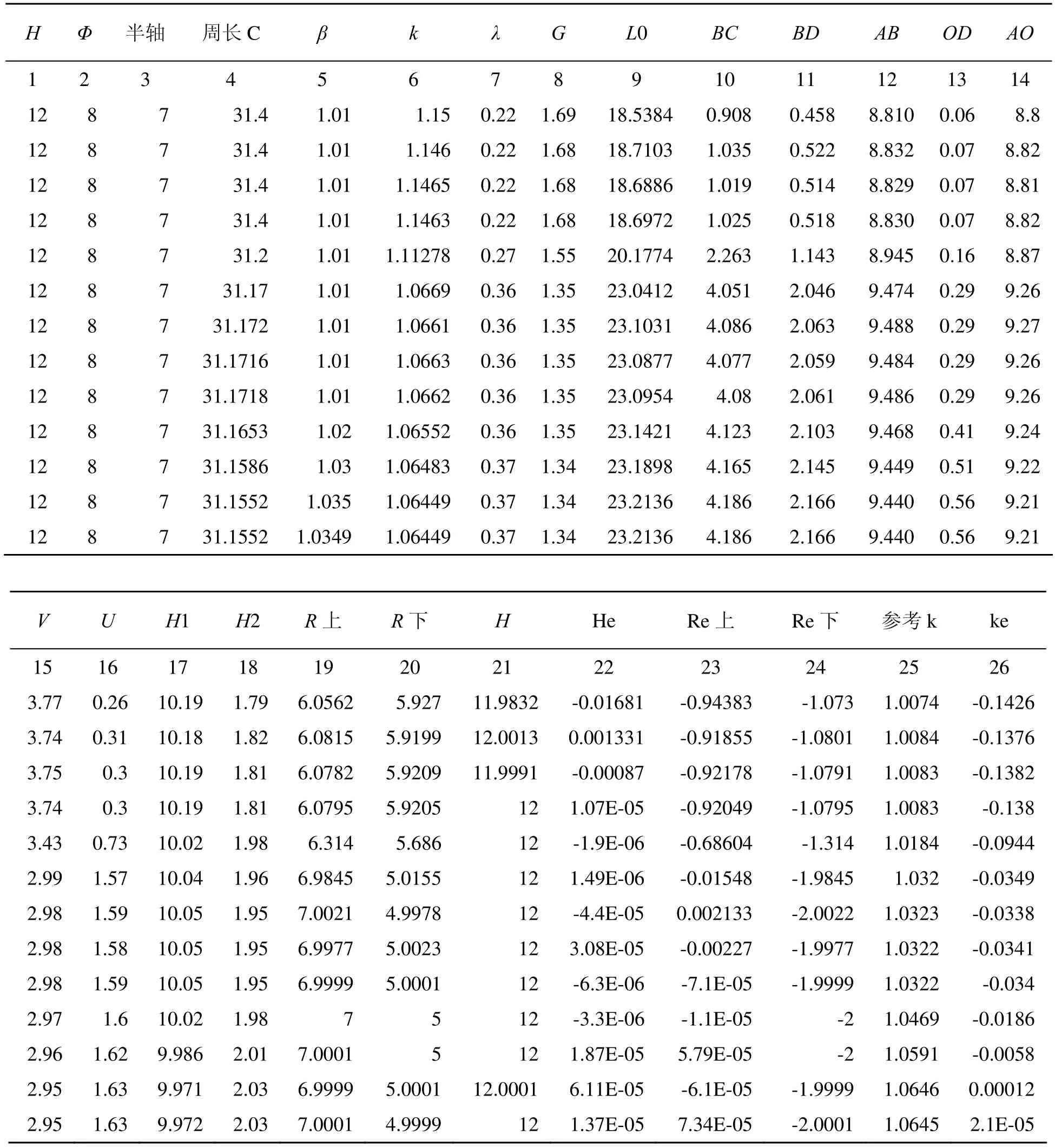
表2 卵圆参数计算示例

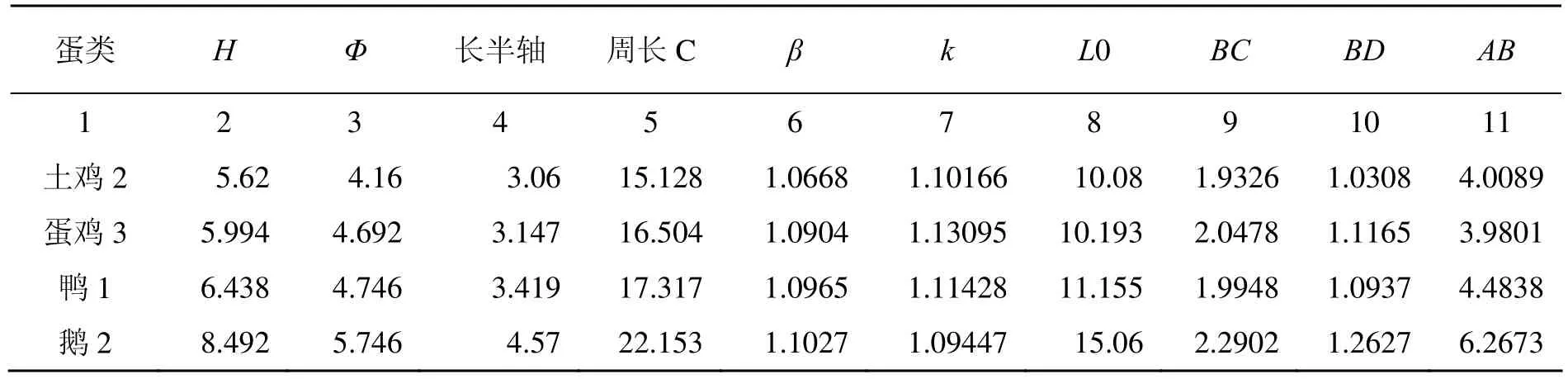
表3 家禽卵（蛋）参数分析

OD AO BC上长 BC下长 上半轴 下半轴 H He Re ke 12 13 14 15 16 17 18 19 20 21 0.359 3.8908 4.4168 1.2032 3.0601 2.56 5.6201 6.3E-05 5.65E-05 -2E-06 0.4451 3.8461 4.5333 1.4607 3.147 2.847 5.994 -7E-06 -2.4E-06 -8E-05 0.4486 4.3715 5.0232 1.4148 3.419 3.019 6.438 -6E-06 -1.9E-06 8.3E-05 0.5321 6.1618 6.8841 1.608 4.5699 3.9221 8.492 4.8E-05 -5.7E-05 5.1E-05

图17 家禽卵参数作图与实物比较图

家禽卵（蛋）的单一个体，属于和标准卵圆近似的普通卵圆。虽然测量和手工作图误差较大，图形与实物基本吻合，说明分析方法的可行性。若能找出与椭圆类似的卵圆族，分析结果将更加逼真。

实例说明，任意一组特征参数，能够计算出标准卵圆的参数和作图，为图形设计提供有效方法。

6 多焦点圆及其椭圆和卵圆的应用前景

多焦点圆及其椭圆和卵圆的图形，具有稳固性、对称性、方向性、多样性。适用于广泛的图形设计：（1）均匀介质中运动物体的外形设计。（2）水中漂浮物的外形设计。（3）薄壳结构的设计。（4）机械、日常用品、玩具、广告、工艺品等方面的图形设计。

在相关学科中涉及到椭圆和卵圆图形分析，为指导科学研究和生产管理服务：（1）通过对动物和家禽卵（蛋）的形状分析，研究动物和家禽的遗传与进化。（2）通过对植物类圆形果实的形状分析，根据形状的变化，研究品种的遗传和生产管理措施。（3）可能在自然和天文学上得到应用。

7 总 结

椭圆是具有两条对称轴、两个特征参数，规范标准的闭合曲线。有线形两焦点和棱形四焦点两种类型。棱形有形和量的变化，形成特征参数（长和宽）相同，图形不同的多种棱形焦点椭圆。把具有相同特征参数的椭圆称为椭圆族，线形两焦点椭圆是其中的一种。

卵圆是具有一条对称轴、三个特征参数，规范标准的卵形闭合曲线；标准卵圆是特定条件的纺锤形四焦点圆，纺锤形确定卵圆的图形特征；参数和特征参数能够确定同一个卵圆。

圆、椭圆、卵圆和多轴圆的共同特征是：具有相同的形成原理、同属于规范标准的闭合曲线；不同的是焦点的数目和焦点环线的形状。多焦点圆的原理和方法，对四种圆的形成和图形特征有了整体上的基本认识，深度认识有待进一步研究。

[1]刘绍学. 数学2圆与方程[M]. 北京: 人民教育出版社, 2007: 118-122.

[2]刘绍学. 数学选修2—1椭圆[M]. 北京: 人民教育出版社, 2007: 38-40.

[3]百度百科. 椭圆周长[EB/OL]. http://baike.baidu.com/view/1284699.htm, 2007-11-30／2012-10-26