回旋振荡管准光模式变换器的研究与设计

王 虎 耿志辉 徐寿喜 沈文渊 刘濮鲲

（1.中国科学院高功率微波源与技术重点实验室，中国科学院电子学研究所，北京100190；2.中国科学院大学，北京100190；3.北京大学信息科学技术学院，北京100871）

引 言

近年来受毫米波主动拒止系统研究的影响，具有横向输出结构的95GHz回旋振荡管成为国内外研究的热点［1-2］.目前高功率（MW 级）连续波回旋振荡管均采用横向输出结构，相对于轴向输出，采用横向输出结构的回旋管具有多方面的优势.首先，其内置准光模式变换器可以方便地将回旋管高阶工作模式转换为适合于自由空间传输的高斯模式，将能量直接辐射或馈入天线系统，避免了使用尺寸巨大的外接波导模式变换器.其次，横向输出结构将高频能量与电子注分离，一方面可以自由地设计降压收集极，一方面又可以避免被输出窗反射的能量返回互作用腔，影响互作用的稳定性［3］.同时，由于开放式镜面结构具有很高的功率容量，使得准光模式变换器在高功率回旋管的内部能量输出、外部能量传输、以及其他高频率高功率微波器件能量传输方面具有重要的研究价值和广泛的应用前景.

回旋管横向输出方式的核心技术在于内置准光模式变换器的设计，它一般由一个波导末端开口的辐射器和多面聚焦反射镜构成.俄罗斯科学家S.N.Vlasov最早将其应用于回旋管中［4］，此后针对不同的工作模式，相继出现了多种不同类型的辐射器，如斜切型、阶梯型、螺旋型等.为了计算辐射器的辐射场和镜面散射场，B.G.Danly等提出了等效像源的方法，但计算精度不高［5］.为了提高计算准确性，J.Braunstein和 H.Beggs等人利用有限元（Finite Element Method，FEM）法和时域有限差分（Finite Difference Time Domain，FDTD）法来模拟模式的变换过程，但对于高过模波导结构，计算效率明显降低［6-7］.目前国外在该领域通常采用Surf3D软件来模拟，其底层算法为矩量法（Method Of Moment，MOM），虽然结合多层快速多级子算法（Multilevel Fast Multipole Method，MLFMA）［8］提高了计算速度，但其计算效率仍然较低［9］.本文采用数值离散的方法，利用基于惠更斯原理的斯特拉顿-朱（Stratton-Chu）方程和物理光学法计算辐射器的辐射场和镜面散射场，在计算精度和计算效率上相比等效像源法和FEM、FDTD、MOM等具有明显的优势.

1 辐射器的理论分析

辐射器，即互作用波导末端切口，设计为螺旋型.由于高功率回旋管的工作模式大多为圆极化的高阶模式TEmn（m≫1，n≫1），这种模式在辐射时与波导轴线及波导壁呈一定的夹角，一般采用几何光学法分析电磁行波在波导内传输及辐射的物理过程［10］.

工作状态下回旋管互作用腔处于多模共存状态，除工作模式外还存在其他竞争模式.但是由于竞争模式的含量较低，一般在理论分析和计算螺旋切口辐射器的辐射场时只考虑工作模式，忽略竞争模式的影响.通过优化设计互作用波导与辐射器的过渡段可以有效抑制反射波，因此对辐射器进行模拟时仅考虑前向波，忽略反射波的影响.分析和设计螺旋切口辐射器的关键是对圆波导内圆极化电磁波的波矢量进行精确的分析，因为螺旋切口辐射器的主要参数，如螺旋线倾角、开口角度、切口长度等都是基于波矢量来确定的.

假设时谐因子为e-jωt，考虑左旋的横电波TEmn，圆波导中电场的表达式为

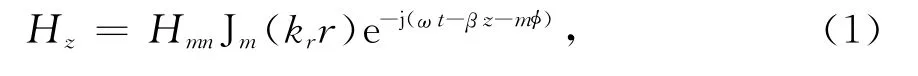
式中：Hmn为传播模式的幅值系数，其大小由该模式的输入功率决定，计算时采用归一化功率的方法得到；Jm为m 阶第一类贝塞尔函数；kr＝χmn/Rw，χmn为J′m（krr）的第n个非零根，Rw为波导半径；β＝为电磁波的角频率，c为真空中的光速；η0为自由空间波阻抗.

第一类贝塞尔函数可由两类汉克尔函数表示为

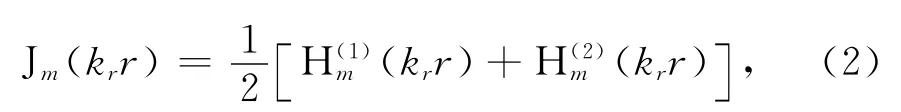
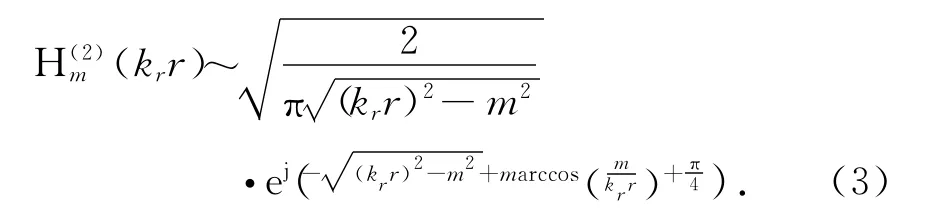
外向传播电磁波的相位可以表示为

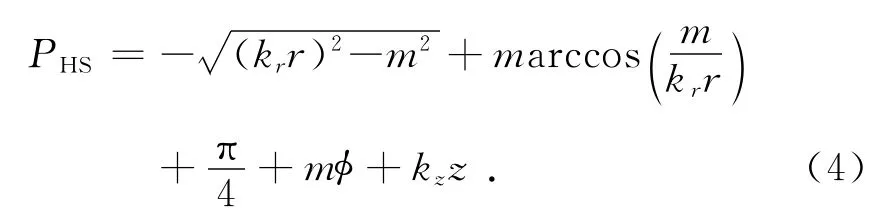
在波导末端的切口处，电磁波向外空间辐射，将辐射的能量看作由无数射线构成的波束，其射线传播方向即波矢量可由式（5）得到，其中C为常数.

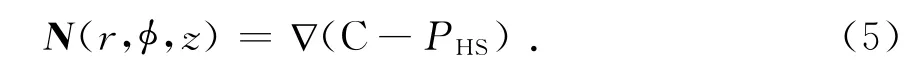
螺旋切口辐射器如图1（a）所示.根据几何光学原理，辐射器的切口角度可以表示为

所有电磁射线最终均经过矩形口径向外空间辐射，如图1（b）所示，计算时将该矩形口径作为螺旋切口辐射器的等效辐射源.矩形口径的轴向长度即为辐射器的切口长度.根据能量守恒的观点，矩形辐射面辐射的能量等于圆波导输入的能量，据此可以推导得到辐射器的切口长度［12］

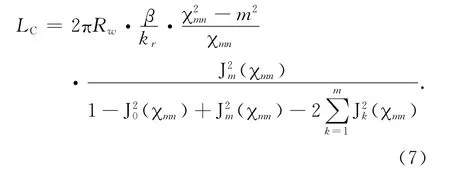
2 聚焦反射镜的设计

互作用后的高频能量经螺旋切口辐射器辐射后，经过聚焦反射镜的聚焦、引导和反射，在输出窗上形成准高斯模式.在设计反射镜形状和优化位置参数时主要考虑聚焦波束与目标波束的相关度和回旋管内部空间区域限制等因素.本设计采用了三反射镜结构，第一级反射镜（M1）为准椭圆柱面，将辐射器辐射后的能量在横向（X向）进行聚焦.第二级反射镜（M2）为抛物柱面，对M1反射的能量在轴向（Z向）进行聚焦.第三级（M3）为抛物面，用来调整波束在横向和轴向的聚焦，同时使出射波束垂直于输出窗.如图2所示，在设计M1时主要依据出射波束在聚焦点处相位相等的原则，也称为零相位差条件，使不同出射波束（1，2）经过M1的反射和聚焦后在另一焦点（P）的相位保持一致，文献［13］给出了准椭圆柱面方程详细的推导过程，此处不再赘述.

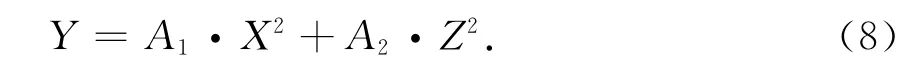
式（8）为抛物面M3的表达式，M3在横向及轴向采用不同的焦距，其中令A1＝0即可得M2的表达式.当A1＜0，A2＞0时，M3即为超环面，根据不同的工作模式和镜面的空间分布合理设置A1的值.辐射器及聚焦反射镜的空间分布如图3所示，详细设计参数见表1，其中给出了反射镜中心位置的空间坐标.为使输出波束在输出窗上的高斯基模含量更高，同时使波束严格垂直于轴向输出，在优化镜面参数时需要对镜面以中心坐标为轴沿X或Z方向旋转一定的角度.由于在优化参数时考虑到工程设计中回旋管内部空间尺寸的限制，表1中所列数据并非理论最优值.由于矩形口径面上的场均匀分布，螺旋切口边缘的衍射效应明显，为减小管内功率损耗，M1的角向尺寸应覆盖从0°～180°的空间.在优化过程中，发现准椭圆面的长轴对结果影响较大.

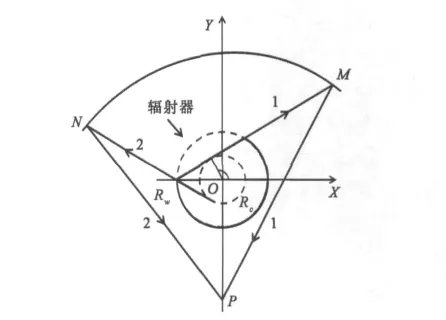
图2 准椭圆柱面聚焦波束的几何光学描述

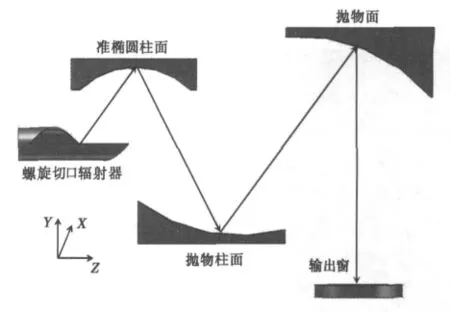
图3 准光模式变换器结构示意图

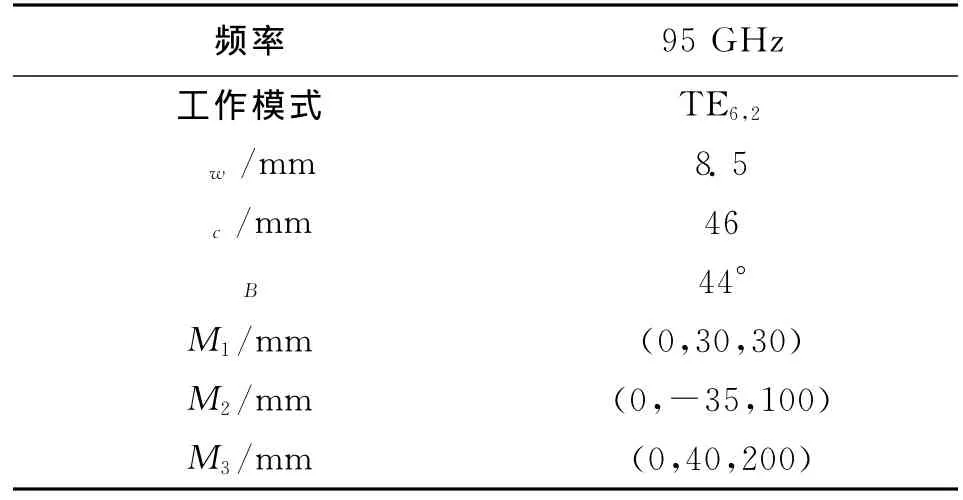
表1 辐射器及反射镜的设计参数

3 数值模拟

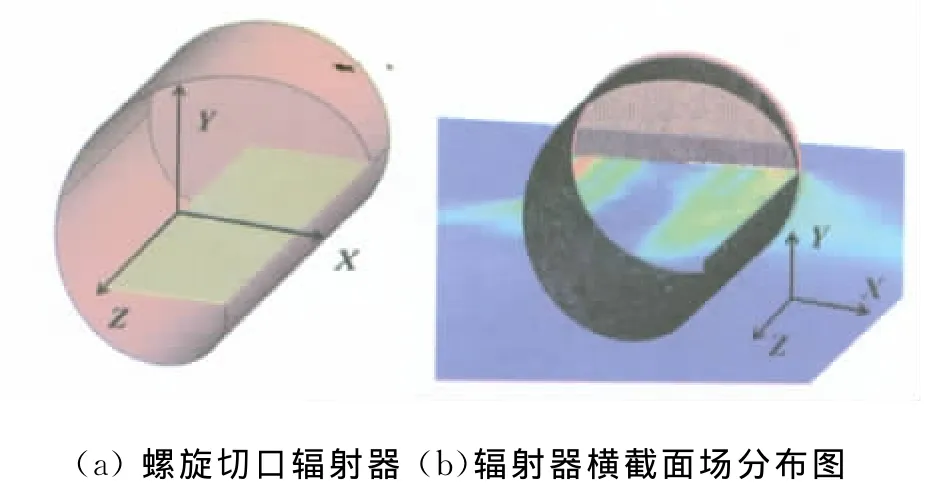
图1 螺旋切口辐射器及其横截面场分布图

由于设计的准光模式变换器的辐射源（天线）与准椭圆柱面，以及镜面与镜面之间的距离均位于辐射源的辐射近场范围内，必须采用严格的电磁辐射近场的方法来计算各镜面上的场分布.对于口径天线的辐射近场，基于惠更斯原理的Stratton-Chu方程具有较高的计算精度和计算速度［14］，因此采用Stratton-Chu方程来计算辐射器的辐射场.同时，考虑到准光学模式变换器的工作频率较高，电尺寸较大，且结构不对称，现有的商用电磁仿真软件对计算资源的消耗很大，且计算效率低，必须采用数值离散的方法模拟模式变换的全过程.利用面等效源时，如果认为金属背面上的等效源为零，在金属面与口径交界边缘处一定存在线电荷和线磁荷，以保持等效表面电流及表面磁流的连续性.如果不考虑线电荷和线磁荷的影响，计算将会带来误差.由于主要求解辐射器（天线）的主瓣和高电平副瓣，不考虑低副瓣和后向辐射，所以采用Stratton-Chu方程计算口径天线的辐射近场是合理的.求解M2及M3以及输出窗上的场分布采用高频近似的物理光学法.根据入射磁场H′求得镜面上的表面感应电流，由边界条件可知，理想导电镜面在电磁场作用下产生的表面感应电流JS为

然后，根据该表面感应电流计算其辐射场.由于反射镜面外表面上的感应电流很小，对镜面内侧的辐射场影响可以忽略，这样即将计算理想导电体的散射场转化为计算导体表面感应电流的辐射场.根据以上方法，编写了快速数值计算程序，针对实际工程需要，对圆极化的TE62模进行了模拟和优化设计，得到了M1，M2，M3上的场分布和各反射镜面的传输效率.如表2所示，三个镜面的传输功率损耗均低于2%.

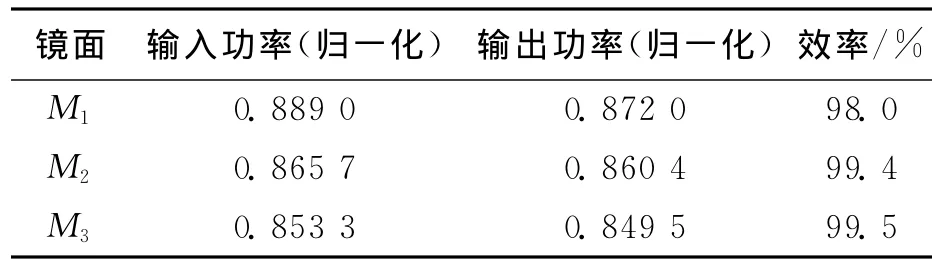
表2 三个反射镜面的传输效率

图4、图5和图6所示依次为准椭圆柱面、抛物柱面和抛物面反射镜上的电场幅度分布，从图中可以看出，由辐射器辐射出的波束经过反射镜的反射和聚焦后，变换为能量集中的准高斯模式.波束半径在变换的过程中不断接近目标高斯基模束腰的预定值（ω0＝12mm）.

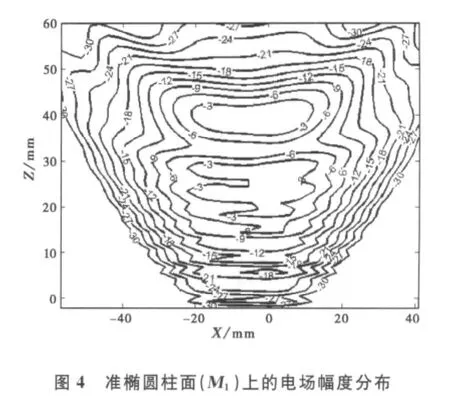
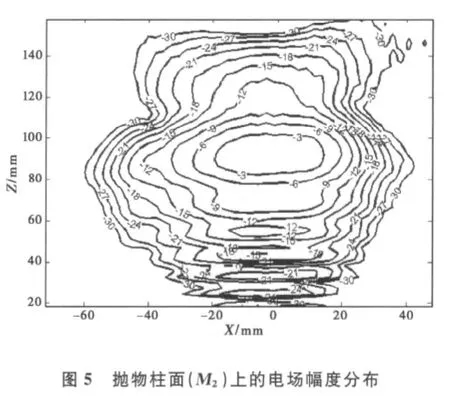
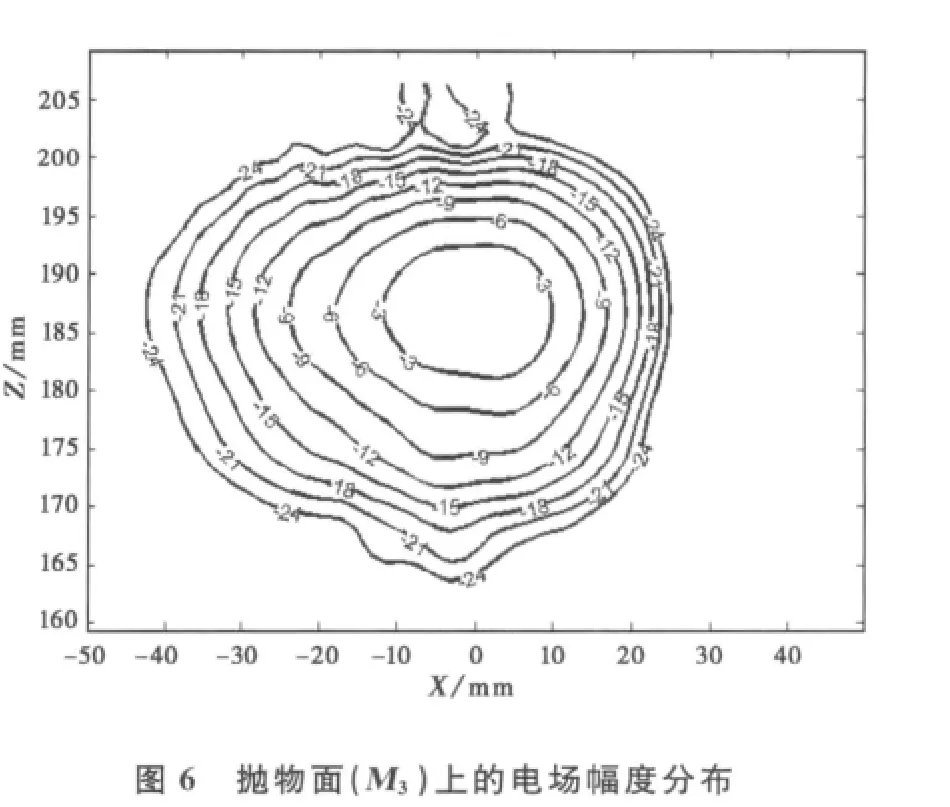
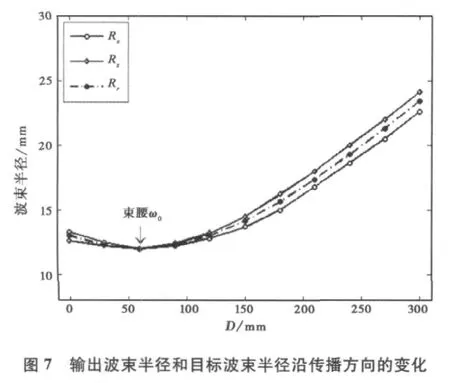
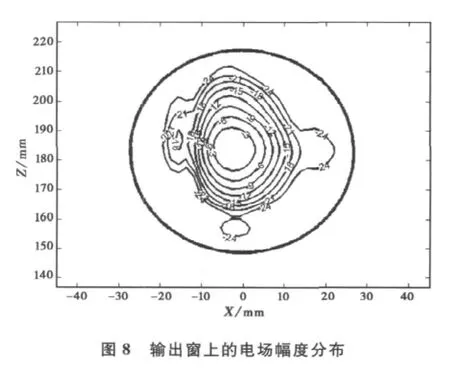
图7给出了输出波束在垂直于Z方向上波束半径随传播距离的变化关系，与理想高斯基模的波束半径比较后发现，在D＝60mm处输出波束与理想高斯基模波束半径的一致性最好，因此将输出窗放置在D＝60mm的位置.输出窗上的场分布如图8所示，图中标出了输出窗（φ＝60mm）的范围.经过三个反射镜的反射和聚焦后，在输出窗上得到了较为理想的场分布，波束束腰为12mm.

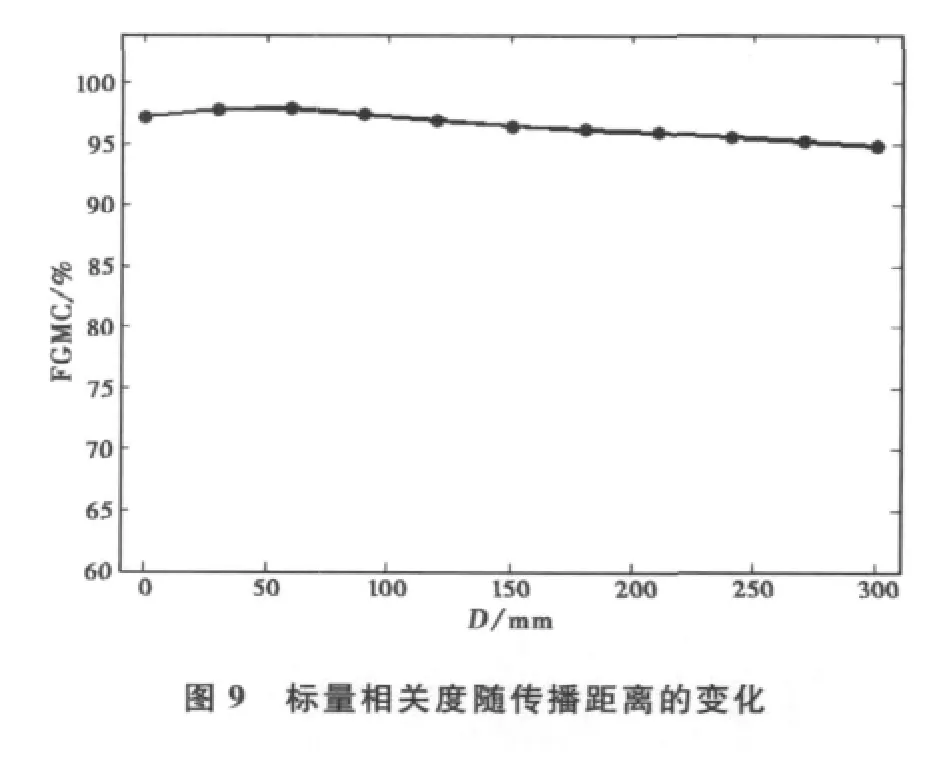
为了更加严格地计算转换器的模式转换效率，采用相关度来表示输出波束中高斯基模含量（Fundamental Gaussian Mode Content，FGMC），如图9所示，标量相关度在0～300mm的范围内均大于95%，在束腰处最高为98%.结合表2中各镜面上的归一化功率值，经计算可得，准光模式变换器的高斯基模转换效率为81.5%.

需要指出的是，由于螺旋型切口的衍射范围较大，因此M1在横向的设计尺寸比理论值要大许多，但是这样仍然难以反射所有的波束.辐射器的衍射损耗过大也是限制模式转换效率的主要因素.从表2中可以看出，大约11%的功率没有到达M1，这部分功率将以热的形式耗散掉.要进一步提高模式转化器的转换效率需要采用更为复杂的波纹波导辐射器.

4 结 论

设计了一种新的三反射镜准光模式变换器，详细推导了螺旋切口辐射器的主要参数，给出了聚焦反射镜的设计原则及反射镜面的关键参数.根据Stratton-Chu方程和物理光学法开发了计算辐射器辐射特性及反射镜面辐射场的数值计算程序，并利用该程序，针对回旋管工作模式TE62模，得到了反射镜面及输出窗上的场分布，输出波束中高斯基模含量达到98%，模式转换效率为81.5%.本研究为设计更高效率的准光模式变换器提供了参考.

［1］KRISHNA P V，KARTIKEYAN M V，THUMM M.Design studies of the output system of a 95GHz，100 KW，CW gyrotron［C］//12th International Vacuum E-lectronics Conference.Roma，2011：291-292.

［2］施美友，屈 劲，薛长江，等.95GHz回旋管内置准光模式转换器仿真设计［J］.强激光与粒子束，2011，23（9）：2438-2442.SHI Meiyou，QU Jin，XUE Changjiang，et al.Simulation design of quasi-optical mode converter for 95GHz gyrotron［J］.High Power Laser and Particle Beams，2011，23（9）：2438-2442.（in Chinese）

［3］THUMM M K，KASPAREK W.Passive high-power microwave components［J］.IEEE Transactions on Plasma Science，2002，30（3）：755-786.

［4］VLASOV S N，ORLOVA I M.Quasi-optical transformer which transforms the waves in a waveguide having a circular cross-section into a highly-directional wave beam［J］.Radio Physics Quantum Electron，1974，17（1）：115-119.

［5］DANLY B G，KREISCHER K E，MULLIGAN W J，et al.Whispering Gallery mode gyrotron operation with a quasi-optical antenna［J］.IEEE Transactions on Plasma Science，1985，13（6）：383-388.

［6］BRAUNSTEIN J，CONNOR K，SALON S，et al.Analysis of flared end for Vlasov-type antenna：comparison of 2DFinite element analysis with experiment［J］.IEEE Transactions on Magnetics，1994，30（5）：3120-3123.

［7］BEGGS J H，LUEBBERS R J，RUTH B G.Analysis of electromagnetic radiation from shaped-end radiators using the finite difference time domain method［J］.IEEE Transactions on Antenna and Propagation，1993，41（9）：1324-1327.

［8］胡 俊，聂在平，王 军，等.三维电大目标散射求解的多层快速多级子方法［J］.电波科学学报，2004，19（5）：509-514.HU Jun，NIE Zaiping，WANG Jun，et al.Multilevel fast multipole algorithm for solving scattering from 3-D electrically large object［J］.Chinese Journal of Radio Science，2004，19（5）：509-514.（in Chinese）

［9］NEILSON J.Surf3dand TOL：Computer codes for design and analysis of high-performance QO Launchers in gyrotrons［C］//Joint 29th Int Conf on Infrared and Millimeter Waves and 12th Int Conf on Terahertz Electronics，September October 27-1，2004：667-668.

［10］王 斌，刘濮鲲，耿志辉.W波段边廊模回旋管Vlasov模式变换器的辐射场研究［J］.红外与毫米波学报，2010，29（2）：109-113.WANG Bin，LIU Pukun，GENG Zhihui.Investigation on radiation from a Vlasov mode converter for W-band whispering gallery mode gyrotrons ［J］.Journal of Infrared and Millimeter Waves，2010，29（2）：109-113.（in Chinese）

［11］金践波.同轴腔回旋管准光模式转换器［D］.成都：西南交通大学，2005.JIN Jianbo.Quasi-optical Mode Converter for Coaxial Cavity Gyrotron［D］.Chengdu：Southwest Jiaotong U-niversity，2005.（in Chinese）

［12］MOBIUS A W，CASEY J A，KREISCHER K E，et al.An improved design for quasi-optical mode conversion of whispering gallery mode gyrotron radiation［J］.International Journal of Infrared and Millimeter Waves，1992，13（8）：1033-1063.

［13］王 斌，杜朝海，刘濮鲲，等.W波段边廊模回旋管准光模式变换器的研究与设计［J］.物理学报，2010，59（4）：2513-2518.WANG Bin，DU Chaohai，LIU Pukun，et al.Study and design of a quasi-optical mode converter for W-band whispering Gallery mode gyrotron［J］.Acta Physica Sinica，2010，59（4）：2513-2518.（in Chinese）

［14］KONG J A.Electromagnetic Wave Theory［M］.New York：John Wiley Sons，1986：376-385.