等离子体散射分析的改进型交替隐式时域方法

殷 雄 赵振维 张 厚 孙树计 姜聿焘 许志永

（1.空军工程大学防空反导学院，陕西 西安710051；2.中国电波传播研究所，电波环境特性及模化技术重点实验室，山东 青岛266107）

引 言

由于等离子体在各个现代化工业领域具有广阔的应用前景，研究这类色散媒质的电磁特性成为当前非常重要的内容.等离子体作为人们发现的第四种物态，当其与电磁波相互作用时表现出很多不同于一般物质的性质，已在民用和军事等领域得到广泛应用，例如高速飞行器探测［1-2］、等离子体推进［3-4］、等离子体隐身技术［5-6］等等.对等离子体电磁特性的运用技术还有待进一步提高，对它的研发一直备受各国政府重视.因此，研究等离子体这类色散介质的电磁特性，具有非常重要的意义.

时域有限差分（Finite-Difference Time-Domain，FDTD）技术被扩展用于等离子体的电磁模拟，涌现了很多算法，主要有：分段线性递归卷积时域有限差分（Piecewise Linear Recursive Convolution-FDTD，PLRC-FDTD）法［7］、分段线性电流密度递归卷积时域有限差分（Piecewise Linear Current Density Recursive Convolution-FDTD，PLCDRC-FDTD）方法［8］、Z变换-时域有限差分（ZTransformation-FDTD，ZT-FDTD）方法［9］、基于电流密度Laplace变换的FDTD方法［10］以及移位算子时域有限差分（Shift Operator-FDTD，SO-FDTD）方法［11-12］等等.这些方法的时间步长都受到Courant稳定性条件［13］的限制，在仿真电大尺寸或高频的等离子体时速度很慢，效率低.而无条件稳定的交替方向隐式时域有限差分（Alternate Direction Implicit-FDTD，ADI-FDTD）算法因其计算时间步长不受Courant稳定性条件的限制，时间步长可以取得较大而使仿真所用的时间步数大大减少，相对传统FDTD算法提高了计算效率，得到了长足的发展和应用，迄今仍吸引了国际及国内学者的广泛关注［14-16］.一些研究者将ADI-FDTD算法扩展到色散媒质的电磁模拟中［17-20］.文献［19］将关于极化强度P的辅助方程引入Maxwell方程组，提出一种计算非磁化等离子体的ADI-FDTD方法.该方法在整个计算区域采用分裂场表示所有的场分量，故数据处理复杂，计算机内存占用量很大.文献［20］提出了一种适于计算非磁化等离子体的分段线性递归卷积-交替隐式-时域有限差分（Piecewise Linear JE Recursive Convolution-ADI-FDTD，PLJERC-ADI-FDTD）方法，虽然该方法精度较高，但由于涉及耗时的卷积运算，其计算效率并不可观.

本文在Maxwell方程组的基础上，运用中心差分格式离散非磁化等离子体所满足的极化电流密度方程，得到一组辅助差分方程，结合交替方向隐式技术和基于辅助差分方程的完全匹配吸收层，提出了一组改进的计算非磁化等离子体散射特性的时域方法即辅助差分方程-交替隐式-时域有限差分（Auxiliary Differential Equation-ADI-FDTD，ADE-ADIFDTD）方法.该公式推导过程不涉及复杂的卷积运算，也不需将场分量进行分裂处理，因而不仅概念简单，易于编程，而且有效地节约了内存占用量，提高了计算效率.另外，仅需对辅助方程的相关系数进行修改，本文提出的算法可以很容易地推广到其他普通媒质或有耗色散媒质的电磁模拟中，可扩展性强.通过与其他FDTD方法对比，运用算例验证了本文方法的正确性和高效性.在此基础上，采用本文算法分析了非磁化等离子覆盖导体圆柱的散射特性，得出了一些有关等离子体隐身的结论.

1 改进型ADE-ADI-FDTD算法的推导

在碰撞非磁化等离子介质中，Maxwell方程及其极化电流密度辅助方程为［10］：

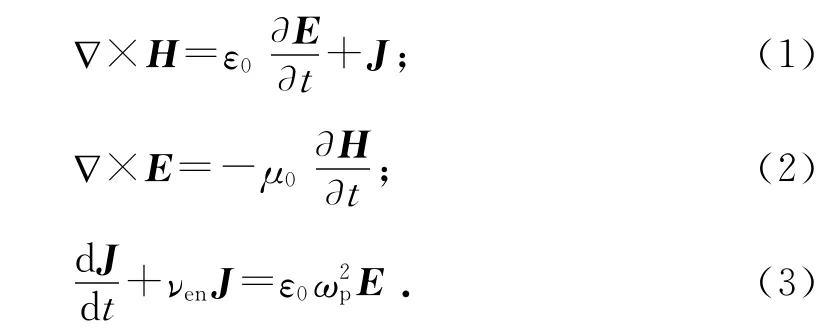
式（3）中ωp，νen分别为等离子体频率和等离子体中电子的平均碰撞频率.

ADI-FDTD方法中的电磁场分量在空间网格的分布方式与传统FDTD方法一致，但需要将原来一个时间步的计算分成两次来进行.分别以两个步骤中的Ex、Hy为例，给出基于式（1）～（3）的三维非磁化等离子体问题的改进型ADI-FDTD迭代公式.

依据公式（1）和（2），从t＝nΔt时刻到t＝（n＋1/2）Δt时刻电磁场旋度方程的离散公式可写为（这里仅考虑Ex和Hy）

第二分步即t＝（n＋1/2）Δt时刻到t＝（n＋1）Δt时刻的电磁场差分迭代公式与第一分步类似，只是相关方程右边场量的显隐格式进行了交换，例如Ex的离散公式为

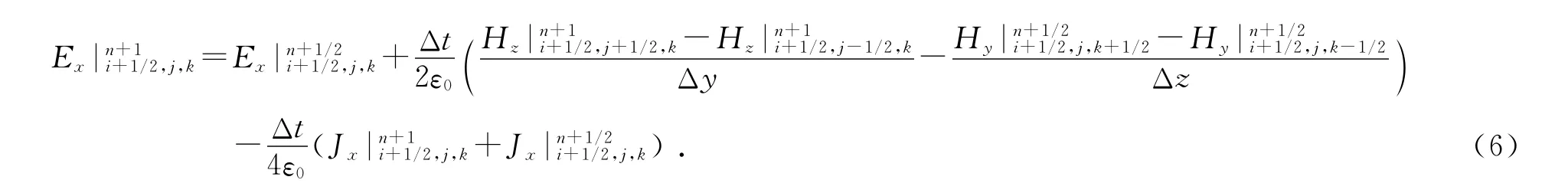
观察式（4）和式（6）可知，极化电流密度J需要作特殊处理.对辅助方程（3）在t＝nΔt时刻到t＝（n＋1/2）Δt时刻采用具有二阶时间和空间精度的中心差分格式进行离散，得到极化电流密度的辅助差分方程为

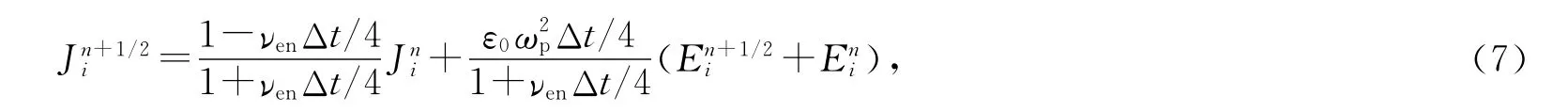
式中i＝x，y，z.这样，极化电流密度的更新可直接由电场得到.从t＝（n＋1/2）Δt时刻到t＝（n＋1）Δt时刻的极化电流密度辅助差分方程具有与式（7）相同的形式，不再写出.将式（7）代入式（4），经适当整理得

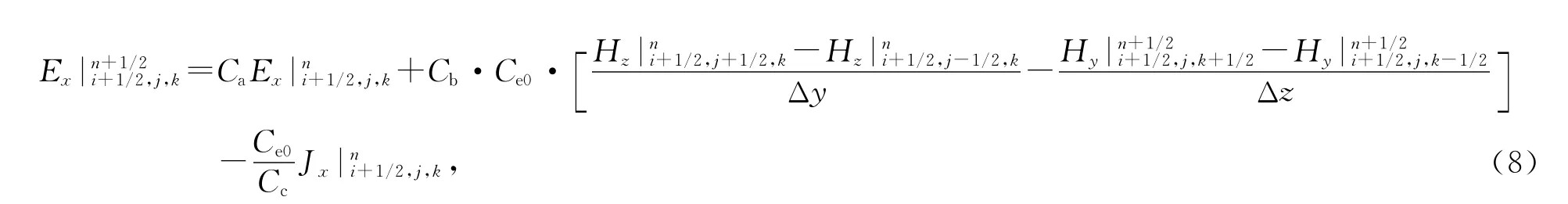
式中：

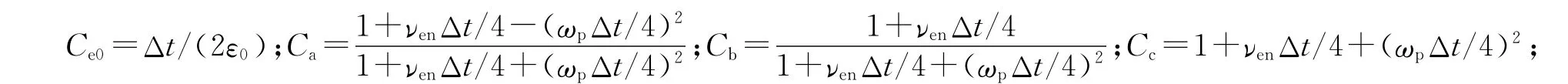
由于式（8）两边具有同一时刻的场分量，不能直接用于数值计算，因此，还需进一步推导适于数值计算的迭代过程.联立式（5）和式（8）消去 Hn＋1/2y，化简得

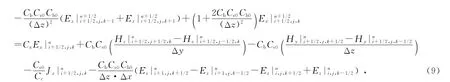
式中：Ch0＝Δt/（2μ0）；Jx｜ni＋1/2，j，k的时 间 步 进 由 式（7）完成.当k沿着z方向从小到大变化时，由式（9）得到一个联立的线性方程组，其系数矩阵是三对角带状矩阵，可用追赶法求解.其余电场分量可用同样的方法得到，且均满足形式如式（9）的方程.求出（n＋1/2）时间步的Ex后，直接解方程（5）即可求得同一时刻的磁场分量Hy.类似的，可以完成（n＋1/2）时间步全部场量的计算.采用同样的方法，可以计算后半个时间步长的全部电磁场分量，在此不再赘述.

对于二维和一维的ADE-ADI-FDTD迭代式，只需在三维迭代式基础上省略相应的无关场量和空间网格标识符k即可.以二维横电波（Transverse Electrical Vave，TE波）第一步迭代为例，省略Ez、Hx、Hy分量和空间网格标识符k后得：

方程（10）是显式的，联合方程（11）和（12），采用前述方法可求得En＋1/2y和Hn＋1/2z，Jnx和Jny的时间步进由式（7）完成.

关于吸收边界的配置，本文采用文献［21］提出的辅助差分方程-完全匹配吸收层（Auxiliary Differential Equation-Perfectly Matched Layer，ADEPML），该匹配层不需要在时域分裂场量，而仅仅在PML区为每个场量添加两个辅助变量，可以和本文提出的场量迭代公式完美结合.本文提出的ADEADI-FDTD算法在整个问题空间采用完整场变量进行迭代计算，而文献［19］为了和PML层中分裂场迭代保持一致，在全部区域将每个场变量进行分裂，生成两个子变量，因而相对文献［19］提出的基于全分裂场的ADI技术而言，本文的算法不仅公式推导简单，操作容易，而且节约近一半的内存占用量.

值得注意的是，本文算法可适用于非均匀媒质，即若ωp和νen随空间位置而变化，那么Ca、Cb及Cc也将是空间坐标（iΔx，jΔy，kΔz）的函数.从推导过程不难看出，改变极化电流密度辅助方程的相关系数，仅对Ca、Cb及Cc的取值产生影响，因而，本文算法可以很容易地推广到其他普通或有耗色散介质.例如，令Ca＝1，Cb＝1，Cc＝1，Ji＝0（i＝x，y，z），本文提出的ADE-ADI-FDTD迭代公式即还原为真空条件下的常规ADI-FDTD迭代式.可见，本文提出的算法具有很好的可扩展性.方法（ZT-FDTD和SO-FDTD）中，令α＝1以满足Courant稳定性条件，本文提出的算法及PLJERCADI-FDTD方法中的α设为3.入射波源为微分高斯脉冲：Einc＝（t-t0）/τ×exp［-4π （t-t0）2/τ2］，其中t0＝70Δt，τ＝140Δt；整个空间分为800个网格，等离子体平板占据中间300～500个网格，其余为空气，两端设为7层PML吸收边界.

图1给出了上述几种FDTD方法计算的电磁波通过非磁化等离子体平板的反射系数和透射系数的收敛数值解.其中，ZT-FDTD方法与SO-FDTD方法各需运行11 000时间步才能达到较好的收敛状态；如果运行的时间步数太少，入射脉冲的时域响应将达不到稳态收敛，以致傅里叶变换后的频域结果不正确.为证明这一点，图2给出了SO-FDTD方法和ZT-FDTD方法各自运行4 000时间步的透射系数计算结果与解析解的对比，由图可知，在0～20GHz频段内两种FDTD方法的数值计算结果严

2 算例验证和性能比较

假设入射波沿z轴正向入射，电磁模型为“空气＋等离子体平板＋空气”，等离子体板厚度为1.5 cm.利用本文提出的改进型ADE-ADI-FDTD算法，文献［20］中的PLJERC-ADI-FDTD方法，文献［9］中的ZT-FDTD方法，文献［11］中的SO-FDTD方法以及文献［12］提到的解析方法对该模型进行计算.

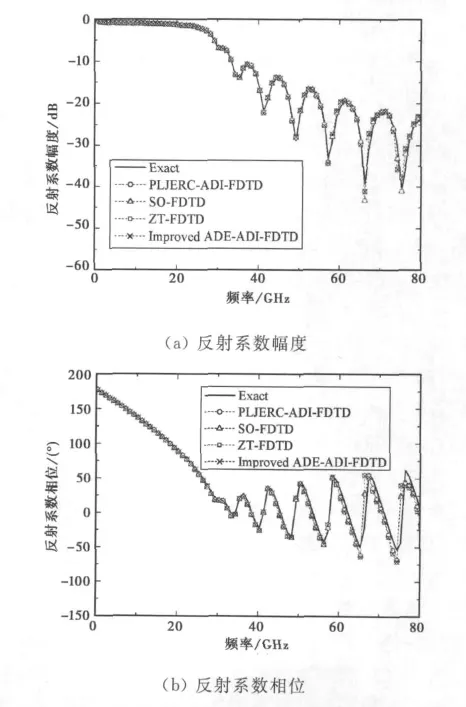
仿真时各种参数选择如下：νen＝20GHz，ωp＝2π×28.7×109rad/s，空间步长Δs取75μm，仿真时间步长Δt＝α·Δs/（2c），c是真空光速，常规FDTD重偏离解析解.而PLJERC-ADI-FDTD方法及本文算法由于选择的时间步长是常规FDTD方法的3倍，各自运行4 000时间步即达良好的收敛稳态，如图1所示.由图1还可知：改进型ADE-ADI-FDTD方法与PLJERC-ADI-FDTD方法的计算结果相当一致，且与解析解吻合得非常好.虽然ZT-FDTD方法与SO-FDTD方法的计算结果也与解析解吻合得较好，但其计算精度要逊于改进型ADE-ADIFDTD方法和PLJERC-ADI-FDTD方法，这从图1（c）、（d）不难看出.

表1列出了上述几种FDTD方法获得稳定收敛解的平均计算时间.表中的计算时间为各种FDTD方法在配置为Intel（R）Core（TM）i5-2400 CPU＠3.10GHz的联想电脑上运行6次，取其算术平均值得到.其中，ZT-FDTD方法与SO-FDTD方法各运行11 000时间步；PLJERC-ADI-FDTD方法及本文算法各运行4 000时间步.由表可知，两种ADI-FDTD方法的计算时间要小于SO-FDTD方法及ZT-FDTD方法，这是因为ADI-FDTD方法摆脱了Courant稳定性条件的束缚，时间步长可以是常规FDTD方法的数倍，因此，仿真的时间步数可以大大降低，计算效率随之提高.数值实验表明，如果进一步增大α值，ADI-FDTD方法的仿真步数将进一步减少，计算效率将进一步提高.但是，时间步长过大时会存在较大的数值色散误差和各向异性误差，导致S参数出现波动.本文实验表明，α的取值一般不应超过6.另外，本文提出的ADE-ADI-FDTD算法由于避免了复杂的卷积运算，其计算效率要高于PLJERC-ADI-FDTD方法.

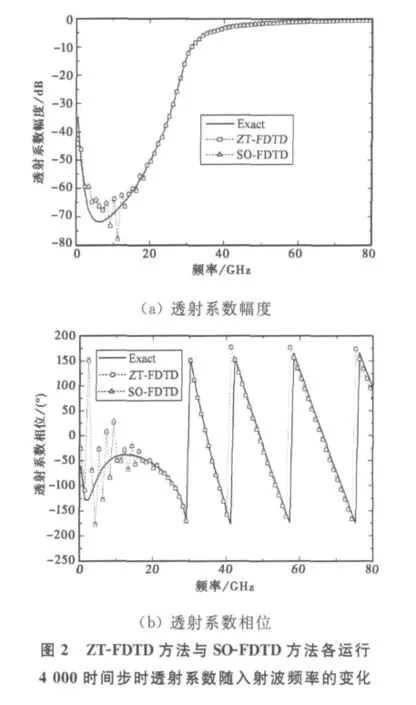
表1 不同FDTD方法计算电磁波通过等离子体平板的平均计算时间

3 非磁化等离子体覆盖导体圆柱的散射特性

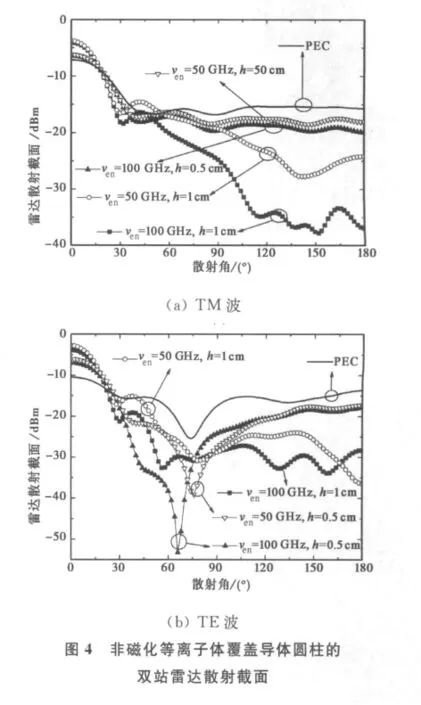
研究电磁波在等离子体中的电磁散射特性，能够给我们合理利用等离子体隐身技术提供理论依据.利用本文提出的算法研究了非磁化等离子体覆盖导体圆柱对入射横磁波（Transverse Magnetic Wave，TM波）（仅有Ez，Hx和Hy分量）和TE波（仅有Hz，Ex和Ey分量）的散射特性.等离子体覆盖导体圆柱的FDTD计算区域及各种边界划分如图3所示.假设入射波频率为15GHz，导体圆柱的半径r为入射波波长λ0的一半即1cm，等离子体涂覆层厚度h分别为0.5cm和1cm，等离子体频率为12GHz，碰撞频率νen分别取50GHz和100 GHz.仿真时选择时间步长控制参数α＝3，空间网格步长Δx＝Δy＝λ0/40，整个问题空间划分为150×150个网格.利用改进的ADE-ADI-FDTD方法计算得到的双站雷达散射截面（Radar Cross Section，RCS）如图4所示（图中导体曲线是指半径为1 cm的导体圆柱对入射波的散射结果，厚度是指等离子体涂覆层厚度）.

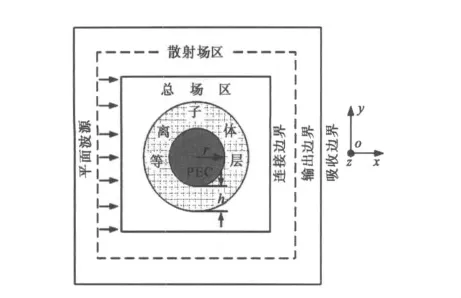
图3 等离子体覆盖导体圆柱的FDTD模型

观察图4可知，对于等离子体圆柱，TE波与TM波散射规律基本一致：与纯导体圆柱的散射相比，非磁化等离子体涂覆层能够较大地减小后向和大散射角范围内的RCS，但对前向散射和小散射角范围的散射却有小幅增强的作用.对圆柱型非磁化等离子体包层来说，等离子体对电磁波的作用主要有折射效应和吸收衰减作用，这是导致后向RCS减小的原因.对于前向附近RCS较大的解释是，就规则目标来说，前向RCS与目标的投影面积成正比关系，若把等离子体包层和导体看作一个整体，其投影面积确实增大了［22］；另外，由于入射波频率高于等离子体频率，电磁波可以以行波的形式到达圆柱的阴影区［22-23］.

由图4还可以看出，当等离子体涂覆层厚度增大时，等离子体覆盖导体的RCS在前向附近增强了，这是由于其整体投影面积增大的缘故；而当散射角较大时，其RCS的下降非常明显，反映出等离子体的折射和吸收作用.在相同的厚度下，等离子体碰撞频率较大时，其RCS总体来看是降低了，但在TE波散射的个别角度范围这个现象是相反的.

4 结 论

提出了一种改进的计算非磁化等离子体散射特性的无条件稳定时域方法即辅助差分方程-交替隐式-时域有限差分（ADE-ADI-FDTD）方法.在此方法中，运用中心差分格式离散极化电流密度和等离子体特征参数所满足的关系方程，得到一组辅助差分方程，避免了复杂、耗时的卷积运算（与文献［20］的PLJERC-ADI-FDTD相比），提高了计算效率.采用ADE-PML，使得本文算法在整个电磁问题空间都不要分裂场变量，相对文献［19］提出的ADI方法而言，不仅操作简单，而且节约了近一半的内存空间.算例的对比计算表明，本文提出的算法不论在精度上还是在效率上都高于普通的Z变换FDTD方法和SO-FDTD方法，在和文献［20］提出的PLJERCADI-FDTD方法保持相同精度的同时取得了计算速度上的优势.通过对辅助方程的关键系数进行修改，本文提出的改进型无条件稳定ADI-FDTD算法可以很容易地推广到其他非均匀有耗色散媒质的电磁模拟中，具有很好的普适性.运用本文算法对非磁化等离子体涂覆导体圆柱的散射特性的分析表明：在相当宽的散射角范围内，等离子体涂覆导体圆柱的RCS与导体圆柱的RCS相比要小很多，特别是大散射角时，这种现象更明显；保持碰撞频率不变时，增加非磁化等离子体涂覆层厚度能够较大地减小后向和大散射角范围内的RCS；而在相同的涂覆层厚度下，等离子体碰撞频率变大时，其RCS总体上呈降低趋势，但在TE波散射的个别角度范围这个变化是相反的.

［1］KIM M，KEIDAR M，BOVD I D.Two-dimensional model of an electromagnetic layer for the mitigation of communications blackout［C］//47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition.Florida，2009：10-17.

［2］MANNING R M.Analysis of Electromagnetic Wave Propagation in a Magnetized Re-Entry Plasma Sheath via the Kinetic Equation［R］.Cleveland：National Aeronautics and Space Administration Glenn Research Center，2009：1-33.

［3］SHANG J S.Plasma injection for hypersonic bluntbody drag reduction［J］.AIAA Journal，2002，40（6）：1178-1186.

［4］罗金玲，徐 敏，戴梧叶，等.高速飞行器等离子体减阻的数值模拟研究［J］.宇航学报，2009，30（1）：119-122.LUO Jinling，XU Ming，DAI Wuye，et al.Numerical simulation investigation on plasma injection for drag reduction of hypersonic vehicle［J］.Journal of Astronautics，2009，30（1）：119-122.（in Chinese）

［5］BESKAR，CHRISTOPHER.R.Cold Plasma Cavity Active Stealth Technology［R］.USA：STAVATTI White Paper，2004.

［6］潘文俊，童创明，周 明.等离子体与等离子体隐身技术［J］.电讯技术，2009，49（8）：108-112.PAN Wenjun，TONG Chuangming，ZHOU Ming.Plasma and plasma stealth technology［J］.Telecommunication Engineering，2009，49（8）：108-112.（in Chinese）

［7］AI X，HAN Y P，LI C Y.Analysis of dispersion relation of piecewise linear recursive convolution FDTD method for space-varying plasma［J］.Progress in Electromagnetics Research Letters，2011，22：83-93.

［8］LIU S，LIU M，HONG W.Modified piecewise linear current density recursive convolution finite-difference time-domain method for anisotropic magnetized plasma［J］.IET Microw Antennas Propag，2008，2（7）：677-685.

［9］晏 明，许 金，余锡文.不均匀非磁化等离子体柱的ZTFDTD分析［J］.海军工程大学学报，2009，21（3）：18-22.YANG Ming，XU Jin，YU Xiwen.ZTFDTD analysis of inhomogeneous unmagnetized plasma cylinder［J］.Journal of Naval University of Engineering，2009，21（3）：18-22.（in Chinese）

［10］YANG Lixia，XIE Yingtao，YU Pingping.Study of bandgap characteristics of 2Dmagnetoplasma photonic crystal by using M-FDTD method［J］.Microwave and Optical Technology Letters，2011，53（8）：1778-1784.

［11］YANG Hongwei.A FDTD analysis on magnetized plasma of Epstein distribution and reflection calculation［J］.Computer Physics Communications，2009，180（1）：55-60.

［12］YIN Xiong，ZHANG Hou，XU Haiyang and ZENG Xianfeng.Improved shift-operator FDTD method for anisotropic magnetized plasma with arbitrary magnetic diclination［J］.Progress in Electromagnetics Research B，2012，38：39-56.

［13］TAFLOVE A，HAGNESS S C.Computational Electrodynamics：the Finite-Difference Time-Domain Method［M］.Norwood：Artech House，2005：302-313.

［14］FU W，TAN E L.Stability and dispersion analysis for ADI-FDTD method in lossy media［J］.IEEE Transactions on Antennas and Propagation，2007，55（4）：1095-1102.

［15］RAMADAN O.An Implicit 4-stage ADI waveequation PML algorithm for 2-D FDTD simulations［J］.IEEE Antennas and Wireless Propagation Letters，2009，8：391-393.

［16］王全民，陈 彬，郭 刚，等.超宽带冲激无线电引线地面回波仿真算法［J］.系统仿真学报，2011，23（3）：469-473.WANG Quanmin，CHEN Bin，GUO Gang，et al.Ground echo simulation algorithm for ultra-wideband impulse-radio fuze［J］.Journal of System Simulation，2011，23（3）：469-473.（in Chinese）

［17］GARCIA S G，RUBIO R G，BRETONES A R，et al.Extension of the ADI-FDTD method to Debye media［J］.IEEE Transactions on Antennas and Propagation，2003，51（11）：3183-3186.

［18］PEREDA J A，GONZALEZ O，GRANDE A，et al.An alternating-direction implicit FDTD modeling of dispersive media without constitude relation splitting［J］.IEEE Microwave and Wireless Components Letters，2008，18（11）：719-721.

［19］汤 炜，胡茂兵.辅助方程-双向隐式差分法的电磁散射研究［J］.电波科学学报，2011，26（5）：904-909.TANG Wei，HU Maobing.Electromagnetic scattering using ADEs-ADI-FDTD method［J］.Chinese Journal of Radio Science，2011，26（5）：904-909.（in Chinese）

［20］常 雨.超声速/高超声速等离子体流场数值模拟及其电磁特性研究［D］.长沙：国防科学技术大学，2009：82-93.CHANG Yu.Numerical Research on Supersonic/Hypersonic Plasma Flow and its Electromagnetic Characteristics［D］.Changsha：National University of Defense Technology，2009：82-93.（in Chinese）

［21］李 毅.雷达隐身目标电磁散射计算与实验研究［D］.长沙：国防科学技术大学，2007：43-47.LI Yi.Study on Electromagnetic Scattering Computation and Experimentation of Radar Stealth Targets［D］.Changsha：National University of Defense Technology，2007：43-47.（in Chinese）

［22］钱志华.等离子体天线的辐射与散射特性分析［D］.南京：南京理工大学，2006：69-101.QIAN Zhihua.Analysis of Radiation and Scattering Characteristics of Plasma Antenna［D］.Nanjing：Nanjing University of Science ＆ Technology，2006：69-101.（in Chinese）

［23］葛德彪，吴跃丽，朱湘琴.等离子体散射FDTD分析的移位算子方法［J］.电波科学学报，2003，18（4）：359-362.GE Debiao，WU Yueli，ZHU Xiangqin.Shift operator method applied for dispersive medium in FDTD analysis［J］.Chinese Journal of Radio Science，2003，18（4）：359-362.（in Chinese）