复杂传输线网络电磁脉冲响应的拓扑分析研究

张 祥 石立华 周颖慧 张 琦

（解放军理工大学 电磁环境效应与光电工程国家级重点实验室，江苏 南京210007）

引 言

为解决复杂电子系统的电磁耦合分析问题，F.M.Tesche、C.E.Baum等人提出了电磁拓扑理论［1-2］.该理论以图论为基础，依据被研究系统的几何结构对其进行拓扑分解，所得到的各个子空间相互独立.整个电磁场耦合问题由此分解为几个不同的空间区域问题，各子空间之间通过孔缝、连接电缆产生相互作用［2］.Baum等人提出的BLT方程［3］为拓扑理论的应用提供了系统分析的工具，从而使得系统的电磁耦合分析避免了传统计算网格划分所需的大量运算，提高了电磁计算的效率，成为一种有效的复杂大系统耦合分析方法［4］.国内外学者对电磁拓扑问题进行了大量研究［5-7］，把BLT方程进行了推广，将电磁场在空间的传播考虑其中［8］以及用于时域计算、非均匀多导体传输线和非线性负载的计算，使得电磁拓扑理论有了更广的应用范围.

虽然目前大量文章研究了传输线系统的电磁脉冲响应问题，但对于大系统和复杂结构的传输线网络开展分析的文献相对较少.而这类系统恰恰是工程中常常遇到的具体问题.本文以引入建筑结构的传输线及在建筑结构内敷设的传输线网络为背景，研究了复杂传输线网络的电磁脉冲响应分析方法.用空间扩展拓扑模型将待求问题进行拓扑分解，采用基于Agrawal模型的传输线BLT方程分析了场线耦合；建立了传输线网络的拓扑模型并分析计算了网络的终端响应，给出此类问题的一般分析步骤，对实际的电磁防护有一定指导意义.

1 传输线网络拓扑结构模型

如图1所示为一类简化的建筑电力网络布局.在电磁脉冲辐照作用下，外部传输线辐射耦合最强，内部传输线也有辐射耦合.文献［9］研究了建筑钢筋结构的屏蔽效能，研究表明，通常的带钢筋网混凝土建筑层对高空核电磁脉冲（High-Altitude Nuclear Electromagnetic Pulses，HEMP）屏蔽效能可达40 dB.因此，建筑层可做“良好屏蔽近似”，即不考虑外界HEMP对室内的辐射耦合.建筑分为L1、D1、D2、U1、U2五部分空间，建筑外部传输线穿过建筑墙壁进入L1室内.配电柜、楼层配电板和分线节点J1、J2、J3、J4分别位于建筑各部分空间，构成了环形电气布线主网络.终端用电设备PC1、PC2、PC3和NB1与电力线网络各节点相连.建筑外部电缆受到HEMP平面波脉冲辐照.电磁拓扑不需要对整个系统结构进行空间网格划分，而是通过构造交互作用关联图，以节点和管道的形式表现电磁能量的传播途径，因而降低了问题分析的复杂性，能够进行系统性能与状态的研究和评估.图1所示网络拓扑结构的构成为：首先由电磁脉冲（Electromagnetic Pulse，EMP）对建筑外部传输线产生辐射耦合，能量由外部进入室内［10］.定义传输线是单芯导体，线缆外部端接匹配电阻［11］；内部是普通三相电力线构成的电气布线网络，网络具有环形和星型混合结构.连接在环形通信主网络上的终端计算机等效为线性负载.传输线在节点J1处将外部的EMP能量引入建筑内网络，通过传导耦合到达终端设备.

图1 受到电磁脉冲照射的建筑电力网络

定义地面为理想大地，单线传输线离地高度为h，线缆终端阻抗为Zl1；建筑内部各段布线具有相同的特性阻抗，模型建立成仅考虑EMP能量耦合线与相同走向地线构成的双平行线，忽略无信号线的影响［12］.通过分析建立了由节点和管道构成的网络扩展拓扑模型，如图2所示.在图2中，线缆管道由实线表示，场传输管道为管道3，用虚线表示.节点1为传输线端点；节点2是传输线通过建筑壁的位置，等效为理想传导节点；节点4在无穷远；节点5为场线耦合点，位于管道1的中点，用实心矩形表示.线缆管道节点存在入射电压和反射电压，场传输管道存在入射电场和反射电场，以Eref3，5为例，3代表管道编号，5代表节点编号，ref代表反射电场.入射波是平面波并处于无穷远处，则在管道3上，有激励源项S1、S2分别对节点5、4作用，激励源项S1＝S2.

2 传输线网络的终端响应求解

建立网络拓扑结构模型后，需要建立描述各管道间相互关系的拓扑关系方程.对于传输线网络，最关心的是传输线终端负载的感应电压，而BLT方程是求解负载端电压响应的有效方法.室外导线的终端感应电压传导至室内网络，在终端节点处产生响应.

2.1 管道传输方程

在图2所示的拓扑模型中，各条管道中均存在传播的电磁波，由管道的一端节点传播至另一端节点，因此需要对每一条管道建立传输方程.空间辐射管道和线缆传导管道性质不同，但都可以用统一的管道传输方程描述为

式中：P为传输矩阵；E为管道上的激励源矩阵，由Agrawal模型求出.管道Ti（i＝1～11）长度记为Li.

空间电场通过节点5作用在导线上，耦合到节点1、2的电场耦合函数为F2、F1，二者是入射角ψ的函数［8］.因此得到

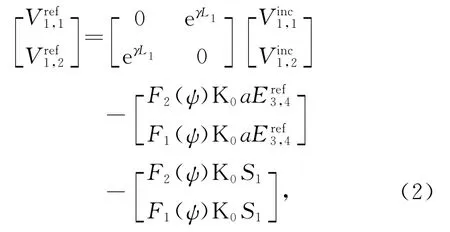
式中：γ为传播常数；K0为源项的格林函数；a为归一化系数，把电场的单位由V/m变化为V.管道2端点为节点2、3，节点2的入射电压Vinc2，2可看作是节点3的反射电压Vinc2，3经管道2传输后的结果.节点3入射电压Vinc2，3与节点2反射电压Vinc2，2同样如此.由此建立管道2的传输方程矩阵为

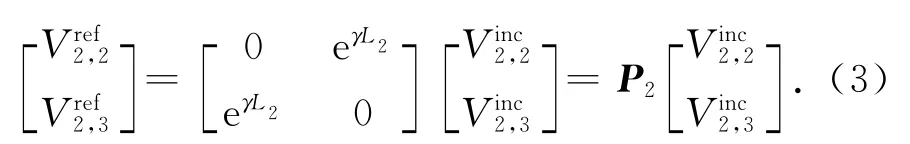
外部传输线受到电场激励，感应电流产生辐射场.管道1对节点4的电场贡献分量可以由节点1、2的入射电压项得到

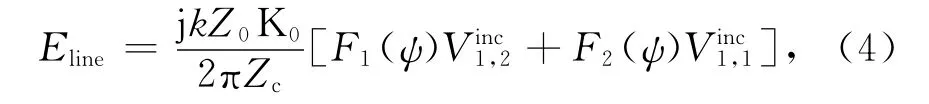
式中：Z0为自由空间波阻抗.则管道3的两个端点电场表达式为

式中：K1、K2为源项的格林函数［13］.考虑到激励源位于无穷远处，产生平面波辐照传输线，节点4同样位于无穷远处自由空间，因此取K0＝K1＝K2.把式（5）和（6）写成矩阵形式有

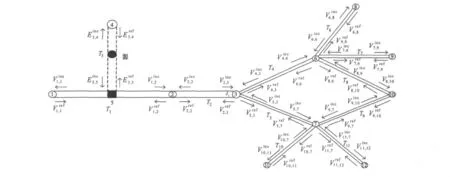
图2 空间拓扑模型与信号流图

同理分析内部各管道，在管道T4至T11上，各管道的传输方程形式与式（3）相同.记Vinc＝［Vinc1，1Vref11，12］T，拓扑结构中管道数量为N，将上述各管道传输方程统一写为一个矩阵形式，有

式中：

B＝［bij］2N×2N＝diag（P1…PN），由式（7）可得到

式（8）的网络传输矩阵方程为

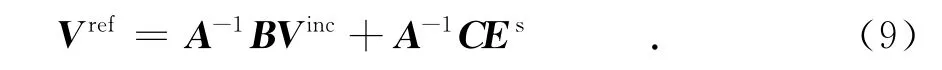
2.2 节点反射系数与散射方程

图2所示的拓扑结构包含了12个节点，要对12个节点分别列出散射方程.拓扑模型中各个节点的入射波和反射波由节点自身的性质所决定.对于节点1有

式中：ρ1是由节点1的负载和传输线特征阻抗定义的反射系数，Zc为传输线特征阻抗.节点8、9、11、12与节点1性质相同，同理求解ρi（i＝8，9，11，12）即可.

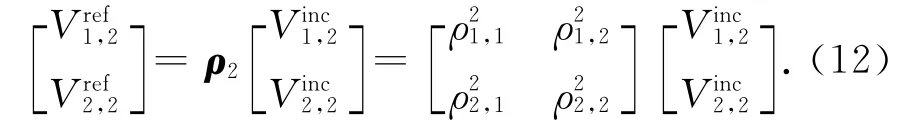
同理，基于基尔霍夫电流定律和基尔霍夫电压定律，分别求出节点3、6、7、10的散射矩阵，其中：ρ3为3×3矩阵，ρ10为2×2矩阵，ρ6、ρ7为4×4矩阵.

节点4是自由空间无穷远处的节点，在这一点可以认为电场无反射，因此

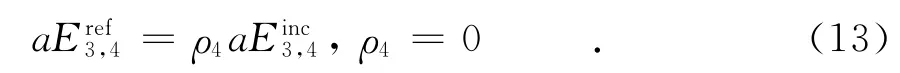
节点5是场耦合节点，只需考虑反射电场，不考虑导线的存在.得到节点5的散射方程为

式中：反射系数为

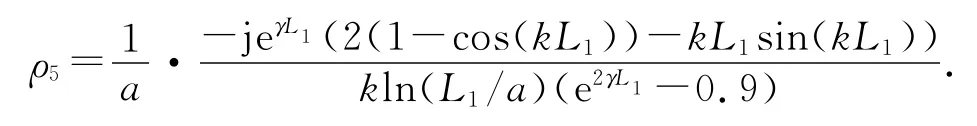
将上述各个节点的散射方程统一写为一个矩阵形式，有

矩阵D是2 N×2 N满置矩阵，其中非零元素由上述各式中的ρ1～ρ11填充.以节点3为例，3×3矩阵ρ3联系了Vref和Vinc的第四项、第七项和第九项，按列顺序依次排列ρ3各项，对应矩阵D的元素d44、d74、d94、d47、d77、d97、d49、d79、d99.

2.3 矩阵求解

定义I为2 N×2 N的单位矩阵，由传输方程式（8b）和散射方程式（14）得到求解终端电压的BLT方程，其形式为

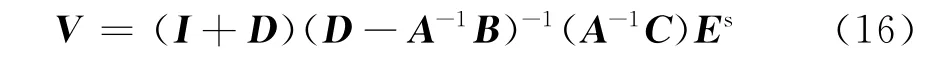
当方程（15）所有所需参数已知时，便可求解该矩阵方程，得到传输线终端在外部电磁脉冲作用下的激励响应.

3 模型验证与结果分析

3.1 场线耦合验证

作为数值验证的例子，采用空间拓扑模型计算文献［13］中理想地面上方单导线响应，单导线传输线的参数为L＝30m，h＝0.1m，a＝0.15m，终端负载为147Ω，入射波为入射角度ψ＝60°，φ＝0°的垂直极化平面波.图3给出了归一化电流复值频谱的幅值，从图中可见计算结果与文献一致.

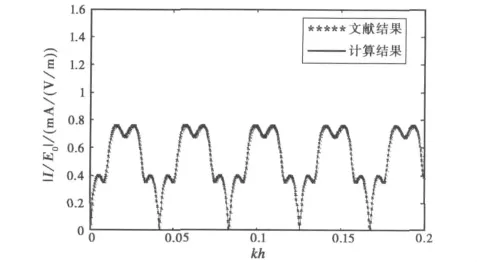
图3 架空单线终端感应电流谱

为说明时域结果的正确性，计算了离地高度0.6m，长度为1m单线的瞬态电流，并与CST仿真软件的结果进行了对比，如图4所示.从图中可见二者是一致的.

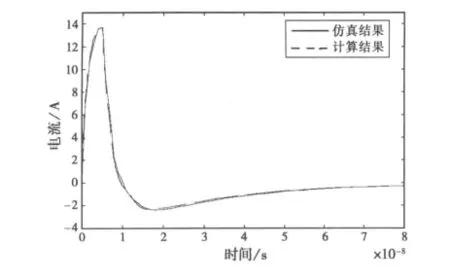
图4 架空单线瞬态电流对比

3.2 终端节点响应与负载影响

定义从外部进入建筑内配电柜的传输线是单线，半径a＝1mm，外部线缆长度30m，内部长度0.3m，离地高度h＝0.1m.建筑内电气布线导体半径1mm，间距3mm，各段线缆具有相同的特性阻抗50Ω.图2中U1室内的设备NB1直接与节点J3相连，因此将其线缆长度定义为0.建筑内线缆T4至T11长度分别为13m、22m、0m、20m、17m、6m、3m、3m.外界EMP脉冲采用双指数脉冲：

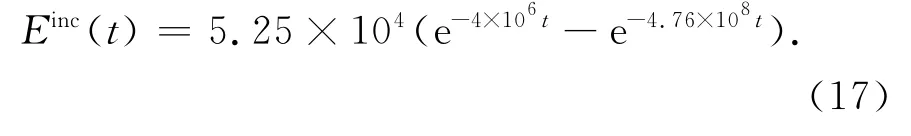
对于单线传输线，以传输线地面的镜像导体作为参考导体，得到传输线特征阻抗为Zc＝60ln（2h/a）＝318Ω，定义线缆端接阻抗为Zc/2.室内线缆分布参数计算由文献［14］给出，将所给参数带入式（15），通过求解BLT方程确定线缆终端的频域响应，再通过Fourier逆变换得到时域波形.图5所示为节点NB1、PC1的时域电压波形.

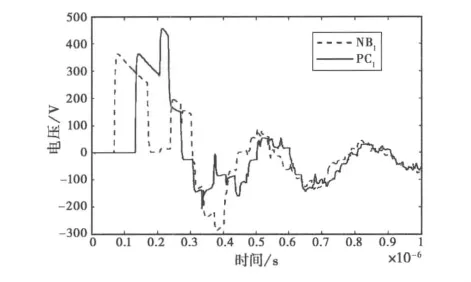
图5 节点NB1和PC1的电压响应

从图5波形可见，节点NB1、PC1的信号经过线缆传输产生了不同的时延.由于终端负载阻抗与传输线特征阻抗不匹配，造成感应电压产生振荡.环形网络产生的谐振作用明显，反映在终端电压上就是信号经过不同路径到达节点后出现电压的叠加，如PC1设备的第二个峰值，由于信号相互叠加而产生了更高的电压峰值.由仿真结果可见：在只考虑HEMP脉冲由外部辐射耦合到传输线网络时，建筑内部的终端设备上会感应出很强的峰值电压，若不加以防护则足以损坏内部设备.

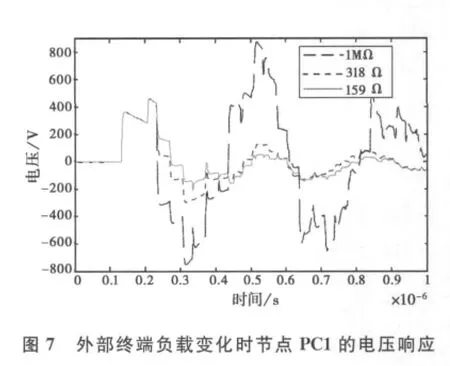
改变建筑内节点PC1的负载，则其终端响应电压发生改变.图6所示为负载值分别为1MΩ、50Ω和25Ω时的终端电压.从图6可见负载大小对电压波形影响很大，其峰值随负载增大而增大.图7所示为建筑外部终端负载值分别为1MΩ、318Ω和159 Ω时，内部节点PC1的终端感应电压.从图7可见，0.2μs之前由于没有反射波的影响波形基本相同，但后续波形由于负载值不同造成振荡和反射，开始出现显著差异.感应电压峰值同样随外部负载的增大而增大.

3.3 网络结构的影响分析

对传输线网络拓扑结构的描述在终端响应分析中是十分重要的环节.计算线缆网络节点上的响应时，整个线缆网络应该整体考虑［4］.如果不能正确的分析网络拓扑结构，得到的结果则不能反映网络的真实响应.例如，对图1的传输线结构作另一种结构划分：外部进入配电柜的传输线作为网络一，内部传输线作为网络二，二者是相互独立的两部分网络.网络一是贯穿建筑内外的单线，在两端加匹配负载，先得到内部节点J1的响应；然后再把此端信号作为新的源信号注入内部的网络二.图8所示为按此拓扑结构得到的内部节点PC1终端感应电压.由于对网络结构进行拆分时改变了图2中节点3的散射性质，结构的改变必然导致整个网络中的信号谐振发生改变，因此此时得到的结果便不再是终端设备的真实响应.只有与线缆的实际连接相吻合的拓扑结构才是正确的.

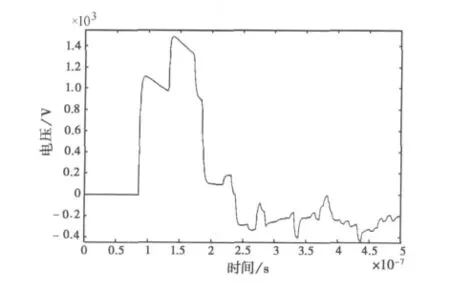
图8 不同结构划分时节点PC1的电压响应

4 结 论

电磁拓扑方法相对于其它方法而言更加简洁高效.文章通过应用电磁拓扑的方法分解系统，得到了基于节点和管道的空间扩展拓扑模型.采用矩阵方程的方式便于计算机进行编程运算，按照BLT方程所包含的各项矩阵逐一进行分析求解，能够方便地分析电磁脉冲作用下建筑内部复杂传输线网络的终端响应.对于存在多个干扰源的问题，则要分别计算只有单一源存在时网络的响应，然后依据叠加定理，对各个单一源存在时的响应波形叠加，得到节点的完整响应波形.同时通过分析计算可知，网络终端的响应与负载的大小关系密切，也为后续的电磁脉冲防护提供了一定依据.

［1］TESCHE F M.Topological concepts for internal EMP interaction［J］.IEEE Trans on EMC，1978，20（1）：60-64.

［2］BAUM C E.Electromagnetic Topology：a Formal Approach to the Analysis and Design of Complex Electronic Systems［R］.Kirtland：Air Force Weapons Laboratory，1980.

［3］BAUM C E，LIU T K，TESCHE F M.On the Analysis of General Multiconductor Transmission Line Networks［R］.Kirtland：Air Force Weapons Laboratory，1978.

［4］ISLAM N E.Application of Advanced Concepts and Techniques in EM Topology Based Simulations：CRIPTE and Related Codes［R］.Missouri：University of Missouri-Columbia，2008.

［5］KIRAWANICH P，YAKURA S J，CHRISTODOULOU C，ISLAM N E.An electromagnetic topology method for cable interactions using a radiating dipole at apertures［J］.IEEE Antennas and Wireless Propagation Letters，2006，5：220-223.

［6］谢鹏浩，刘尚合，谭志良.典型雷达系统的电磁拓扑初步分析［J］.现代雷达，2008，30（2）：17-19.XIE Penghao，LIU Shanghe，TAN Zhiliang.Electromagnetic topological initial analysis of the typical radar system［J］.Modern Radar，2008，30（2）：17-19.（in Chinese）

［7］JUNQUA I，PARMANTIER J P，DEGAUQUE P.Coupling on cables in an electrically large cavity：a theoretical approach［C］//20th Int Zurich Symposium on EMC Proceedings.Zurich，2009：89-92.

［8］TESCHE F M，KEEN J，BUTLER C M.Example of the Use of the BLT Equation for EM Field Propagation and Coupling Calculations［R］.South Carolina：College of Engineering ＆Science，2004.

［9］周璧华，陈 彬，高 成，等.钢筋网及钢筋混凝土电磁脉冲屏蔽效能研究［J］.电波科学学报，2000，15（3）：251-259.ZHOU Bihua，CHEN Bin，GAO Cheng，et al.Study on EMP shielding effectiveness of wire-mesh reinforcement and reinforced concrete［J］.Chinese Journal of Radio Science，2000，15（3）：251-259.（in Chinese）

［10］余同彬，周璧华.贯通导线对屏蔽机箱内电路HEMP耦合电流的影响［J］.电波科学学报，2002，17（5）：481-484.YU Tongbin，ZHOU Bihua.Effects to HEMP induced current in circuits inside the shielding box caused by penetrative wire［J］.Chinese Journal of Radio Science，2002，17（5）：481-484.（in Chinese）

［11］李 莉，冀维林.端接非线性负载的不等长传输线瞬态分析［J］.电波科学学报，2009，24（3）：529-532.LI Li，JI Weilin.Transient analysis of unequal length multiconductor transmission lines loaded by nonlinear devices［J］.Chinese Journal of Radio Science，2009，24（3）：529-532.（in Chinese）

［12］MANSSON D，NILSSON T，THOTTAPPILLIL R，et al.Propagation of UWB transients in low-voltage installation power cables［J］.IEEE Trans on EMC，2007，49（3）：585-592.

［13］TESCHE F M，IANOZ M V，KARLSSON T.EMC Analysis Methods and Computational Models［M］.New York：John Wiley，1997：74-227.

［14］GURU B S，HIZIROGIU H R.Electromagnetic Field Theory Fundamentals［M］.Cambridge：Cambridge University Press，2005：282-295.