改进小波变异粒子群优化算法用于直线阵综合

田雨波 高东慧

（江苏科技大学电子信息学院，江苏 镇江212003）

引 言

阵列天线广泛应用于雷达、无线通信和电子对抗等领域，方向图综合作为阵列天线的关键技术，在抗干扰、参数估计等方面有着重要的作用.文献［1-4］通过粒子群优化算法对电流幅值和相位的连续值进行优化，取得了不错的效果.但在实际应用中可以分别使用数字衰减器和数字相移器对电流幅值和相位进行量化，比如文献［5］用粒子群优化算法对阵列天线电流相位进行量化优化，文献［6］中用改进的遗传算法对连续的电流幅值和量化的电流相位进行优化，文献［7］中对连续的电流幅值量化的电流和6位相位进行优化，同时为了减少相邻阵元间耦合的影响，在目标函数中加入了阵元电流幅值动态范围比，文献［8］中用克隆选择算法对连续的电流幅值和量化的电流相位进行了优化，得到了不错的阵列天线方向图，文献［9］中用蜜蜂算法对量化的电流幅值和量化的电流相位进行优化，该文献把幅值和电流都离散化，取得了不错的效果，但是还有改进的余地.

粒子群优化（Particle Swarm Optimization，PSO）算法是由James Kennedy和Russell Eberhart在1995年提出的一种基于种群搜索的智能优化算法［10］.算法在搜索过程的后期阶段其收敛速度饱和甚至停止，容易陷入局部最优.为了改善PSO算法的性能，避免算法早熟收敛，可以将遗传算法中的变异操作加入到粒子群优化算法中，得到改进的粒子群优化算法.文献［11］中提出了一种基于小波变异的粒子群优化（PSO with Wavelet Mutation，PSOWM）算法，该算法采用了一种基于小波函数理论的新的变异操作，提高了算法的收敛速度和精度，能很好地避免粒子群优化算法陷入局部最优.本文对文献［11］中的算法进行了改进设计，得到一种新的小波变异粒子群优化算法，该算法通过对当前群体最优解有效地运用小波变异操作，并把变异后的值传给当前以一定概率选中的粒子.该算法加大了粒子对整个搜索空间进行搜索的可能性，从而保证改进后的小波变异粒子群算法能够更加快速有效地进行全局搜索.文中首先介绍了IPSOWM算法，然后对直线阵天线在量化幅值和相位情况下进行了综合，结果表明该改进算法在搜索精度及稳定性方面均优于对比文献中结论.

1 小波变异粒子群算法及其改进

文献［11］给出了一种基于小波变异的粒子群算法，该算法的变异功能对粒子起到微调的作用.设每个粒子的变异概率为p∈［0，1］，p的大小根据粒子的维数决定.假设 Xki＝（xki1，xki2，…，xkiκ）是第k次迭代时选中的第i个要变异的粒子，xkiк是该粒子的第κ维，pxmaxi是该粒子搜索空间的上限，pxmini是该粒子搜索空间的下限，则变异公式如下

式中：mut（xkiκ）是变异后的xkiκ；σ是小波函数值，在这里选择Morlet小波函数，其计算公式如下

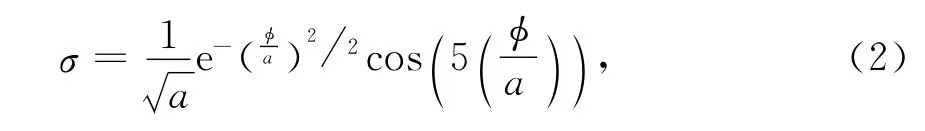
式中φ的取值范围是 ［-2.5a，2.5a］，a的计算公式为

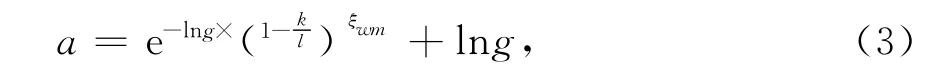
式中：ξωm是单调递增函数的形状参数；g是a的上限值；k是当前的迭代次数；l是最大的迭代次数.

下面对小波变异公式（1）进行改进，得到新的变异公式为

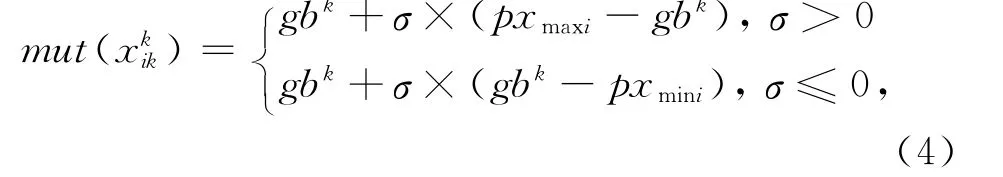
式中：gbk是第k次迭代时的群体最优解；pxmaxi、Pxmini和σ与式（1）中的一样.

式（4）和式（1）的不同之处在于，式（1）是以一定的概率选中某个粒子进行小波变异，变异后的粒子可能还会在局部最优点无法跳出，而找不到全局最优点；而公式（4）则是通过对当前群体最优解进行小波变异操作，然后把变异后的值传给当前以一定概率选中的粒子.因此，该算法能够在当前历史最优解附近进行有效地搜索，从而有效地引导粒子群朝着全局最优点前进，减少每次迭代时粒子陷入局部最优的可能性.关于IPSOWM算法更详细的阐述请参阅文献［12］.

2 直线阵综合

2.1 直线阵综合基本知识

假设N个阵元排列成直线阵，设激励电流为I1＝A1e-jφ1，I2＝A2e-jφ2，…，IN＝ANe-jφN，则该天线的辐射场可以表示为

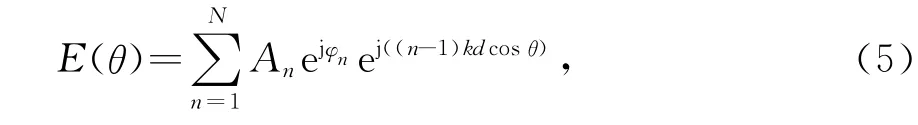
归一化方向函数表示为

考虑2 N个阵元组成的等距不均匀直线阵，阵元间距为d＝λ/2，若电流幅度和相位是对称的，则阵列因子表达式为

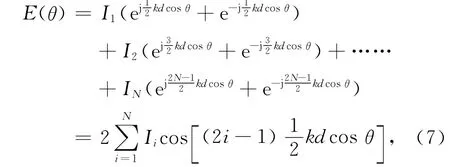
式中：θ是入射信号相对于阵列轴线的方向角；k＝2π/λ为波数.

2.2 直线阵综合实例

本文用IPSOWM算法和PSOWM算法综合直线阵阵列方向图，阵列单元数目20个，激励电流幅度和相位分别在［0，1］和 ［0，2π］范围内变化，考虑到其激励电流幅度和相位的对称性，则算法中每个粒子的维数是20（其中前10位表示电流幅度大小，后10位表示电流相位大小）.算法中种群大小设置为100个，学习因子c1＝c2＝2.05，线性动态惯性权重wmax＝1.2，wmin＝0.1，两种变异算法的变异概率都取p＝0.2，粒子的最大速度vmax＝2.0.在PSOWM算法中形状参数ξwm＝5.0，g＝10 000.在IPSOWM 算法中形状参数ξωm＝0.5，g＝100.

为了减少阵元之间耦合影响，文献［7］中提出了电流幅度动态范围比，它是电流幅度最大值和最小值之间的比值，定义为

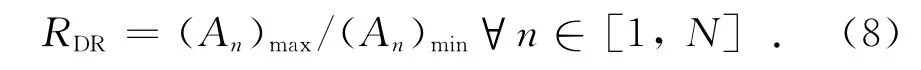
在优化过程中，若数字衰减器的量化位数是m位，则每次幅度值以1/2m变化；若数字相移器的量化位数是n位，则每次相位值以360°/2n变化.

目标函数定义如下

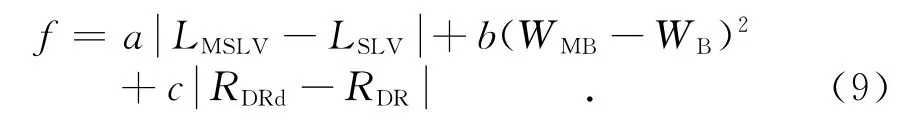
式中：LMSLV、WMB和RDRd分别是算法所优化得到的最高旁瓣电平、零功率波瓣宽度和激励幅度动态范围比；LSLV是设计旁瓣电平；WB是设计的零功率波瓣宽度；RDR是设计的激励幅度动态范围比.在实际仿真中，取a＝0.8，b＝0.2，c＝0.2.

考虑到工程实际，文中主要讨论在量化幅值和量化相位情况下，应用IPSOWM算法和PSOWM算法进行阵列天线综合，算法迭代次数为500次，每种算法分别选取RDR＝5.00，RDR＝10.00两种情况进行优化.

例1 设计指标2 N＝20，LSLV＝-30dB，d＝λ/2，零功率波瓣宽度2θ0＝20°，要求主瓣对准90°方向，电流量化位数5位.算法得到的波束方向图如图1所示，电流分布如表1所示.

图1（a）中PSOWM的零功率波瓣宽度为20°，最大副瓣电平为-30.128 9dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-30.016 6dB，可知PSOWM和IPSOWM分别优化得到的最大副瓣电平都满足指标要求.图1（b）中PSOWM的零功率波瓣宽度为20°，最大副瓣电平为-32.590 8dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-33.305 8dB，可知与 PSOWM 相比，IPSOWM的最大副瓣电平降低0.815 0dB.通过比较图1（a）和图1（b）可知，当RDR取值较大时，算法优化电流幅度的范围比较大，算法优化的结果要比RDR取值较小的好.同时从图1可以看出：当RDR＝10.00时，IPSOWM算法优化的结果明显的比PSOWM算法好.

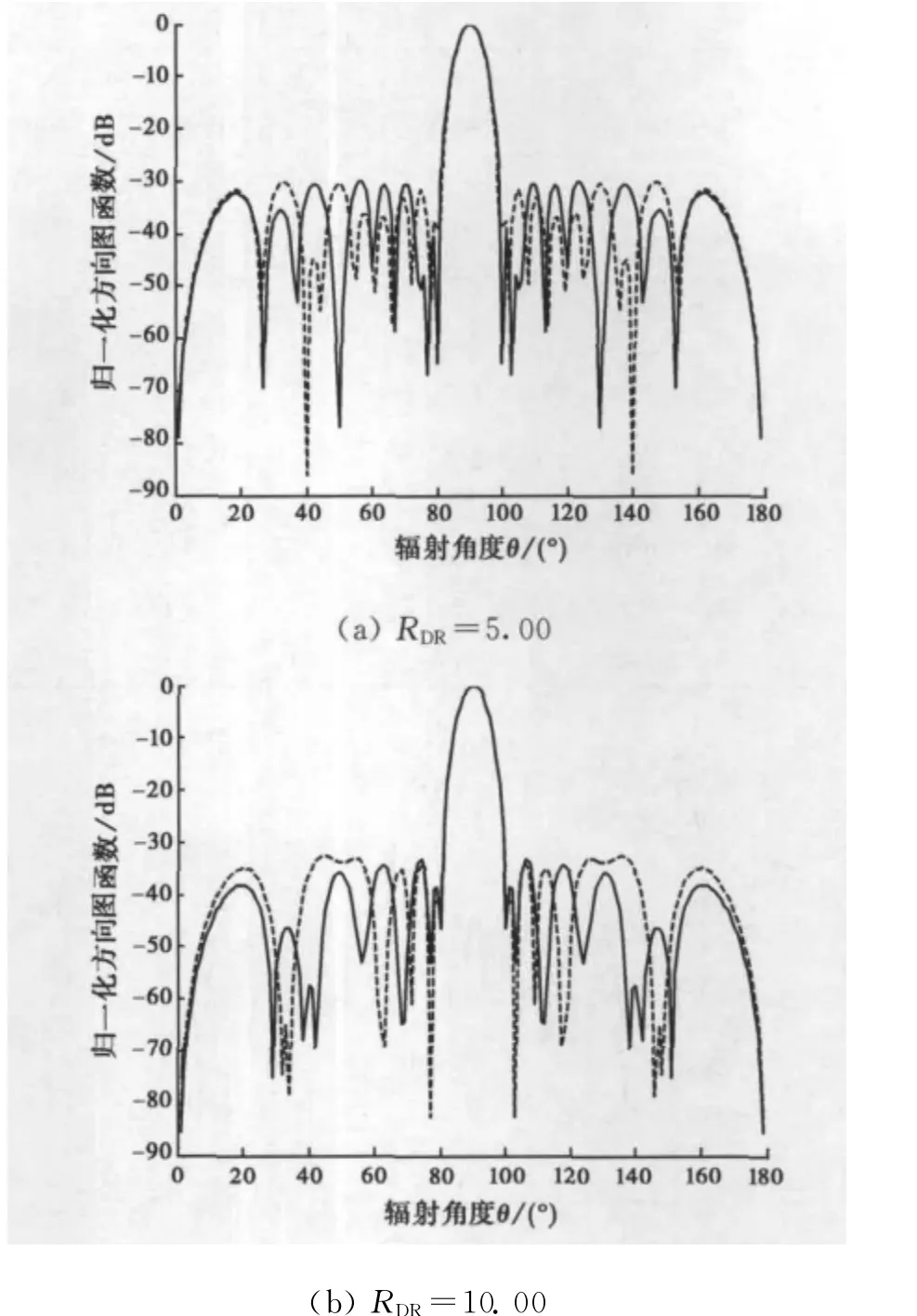
图1 例1中PSOWM（虚线）和IPSOWM（实线）优化得到的波束方向图

例2 设计指标2 N＝20，LSLV＝-30dB，d＝λ/2，零功率波瓣宽度2θ0＝20°，要求主瓣对准90°方向，电流幅值量化位数6位.算法得到波束方向图如图2所示，电流分布如表1所示.

图2（a）中PSOWM的零功率波瓣宽度为20°，最大副瓣电平为-31.422 4dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-31.585 8dB，可知与PSOWM相比，IPSOWM的最大副瓣电平降低0.163 4dB.图2（b）中PSOWM 的零功率波瓣宽度为20°，最大副瓣电平为-31.419 6dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-36.260 8dB，可知与PSOWM相比，IPSOWM 的最大副瓣电平降低4.841 2dB.通过比较图2（a）和图2（b）可知，当RDR取值较大时，电流幅度的范围比较大，算法优化的结果要比RDR取值较小的好.同时从图2中可以看出：当RDR＝10.00时，IPSOWM算法优化的结果明显的比PSOWM算法好.当RDR＝10.00时，比较图1（b）和图2（b）可知，图2（b）中的最大副瓣电平比图1（b）中的低，说明当电流幅度的量化位数越多时，算法优化得到的最大副瓣电平就越低.

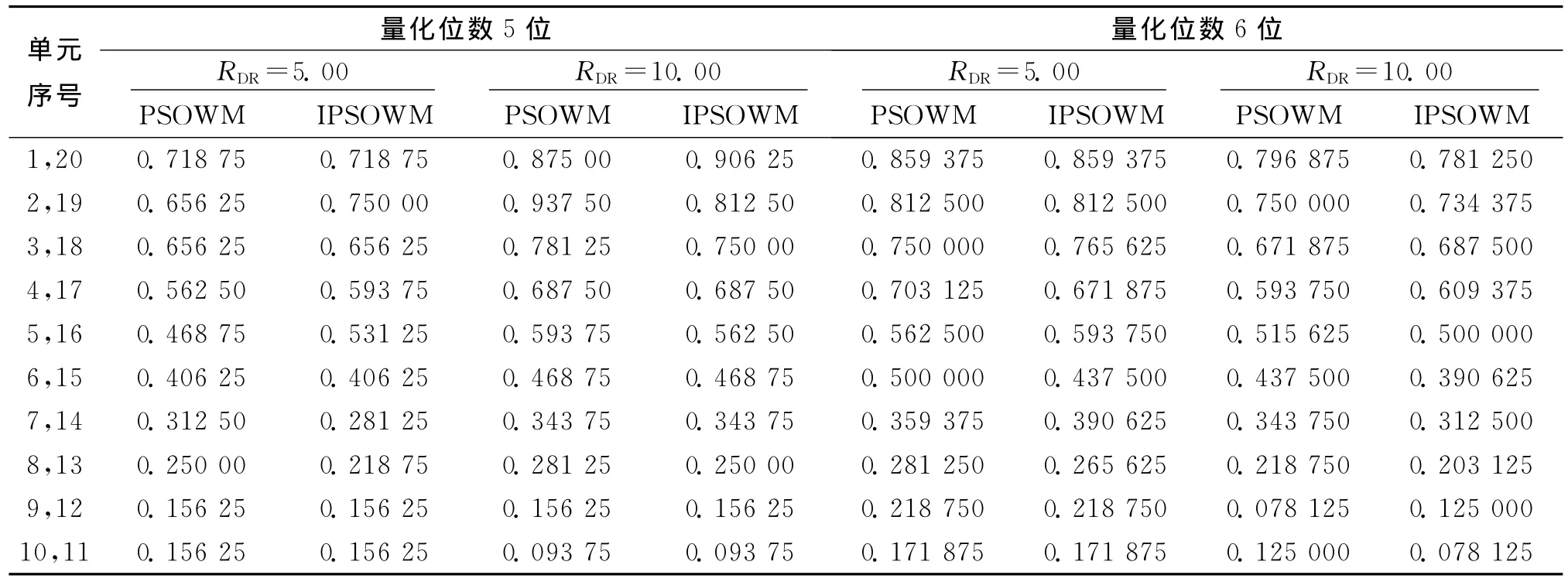
表1 PSOWM和IPSOWM优化的阵元电流幅度分布

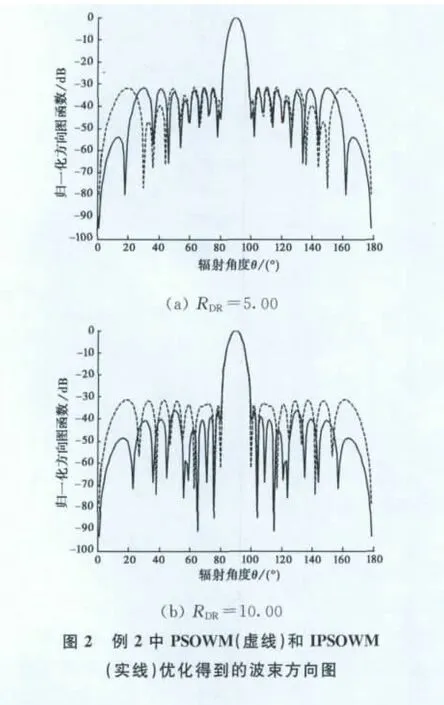
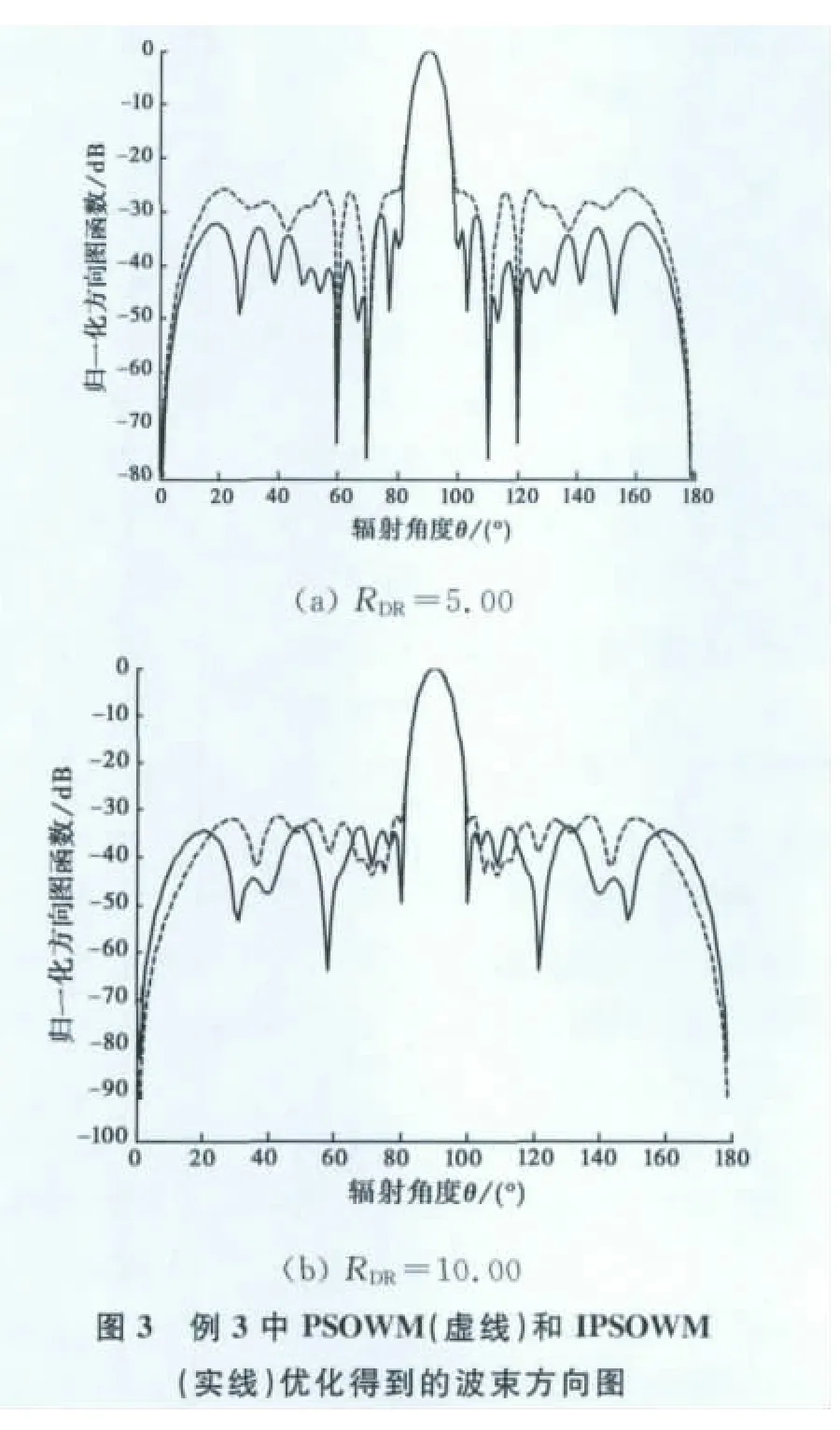
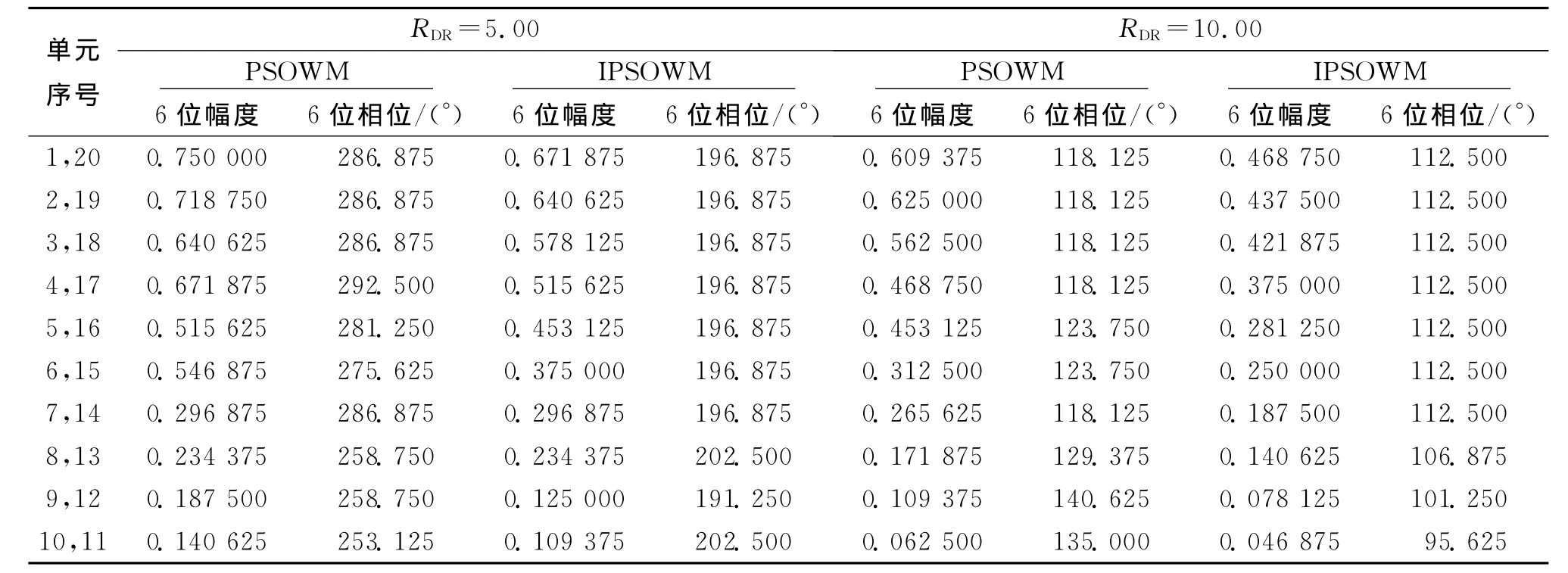
表2 PSOWM和IPSOWM优化的阵元电流幅度和相位分布

例3 设计指标2 N＝20，LSLV＝-30dB，d＝λ/2，零功率波瓣宽度2θ0＝20°，要求主瓣对准90°方向.电流幅值量化位数6位，相位量化位数6位，算法优化得到波束方向图如图3所示，电流和相位分布如表2所示.

图3（a）中PSOWM的零功率波瓣宽度为20°，最大副瓣电平为-25.899 4dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-30.574 5dB，可知与PSOWM相比，IPSOWM的最大副瓣电平降低4.675 1dB.图3（b）中PSOWM 的零功率波瓣宽度为20°，最大副瓣电平为-31.537 0dB，IPSOWM的零功率波瓣宽度为20°，最大副瓣电平为-33.636 7dB，可知与PSOWM相比，IPSOWM 的最大副瓣电平降低2.099 7dB.从图3（a）和图3（b）中看出：当RDR＝10.00时IPSOWM 算法和PSOWM算法优化得到的方向图达到设计指标，同时IPSOWM算法优化的方向图最大副瓣电平更低，证明了该算法改进的有效性.

3 结 论

文中针对PSO算法易发生早熟收敛、陷入局部最优的缺点以及收敛精度低的问题，对文献［11］中给出的基于小波变异的粒子群（PSOWM）算法进行了改进，得到改进的小波变异粒子群（IPSOWM）算法.考虑到实际工程中数字衰减器和数字相移器在阵列天线方向图综合问题中的应用，分别用PSOWM算法和IPSOWM算法在量化的电流幅值和量化的电流相位情况下进行了优化，并对优化后的方向图进行了比较，证明了IPSOWM算法的有效性.尽管论文中只是讨论了直线阵方向图综合，但是进一步工作可以考虑把该方法运用到面阵和共形阵方向图综合问题中去.

［1］KHODIER M，CHRISTODOULOU G.Linear array geometry synthesis with minimum side-lobe level and null control using particle swarm optimization［J］.IEEE Trans AP，2005，53（8）：2674-2679.

［2］金荣洪，袁智皓，耿军平，等.基于改进粒子群算法的天线方向图综合技术［J］.电波科学学报，2006，21（6）：873-878.JIN Ronghong，YUAN Zhihao，GENG Junping，et al.The pattern synthesis of antennas based on a modified PSO algorithm［J］.Chinese Journal of Radio Science，2006，21（6）：873-878.（in Chinese）

［3］焦永昌，杨 科，陈胜兵.粒子群优化算法用于阵列天线方向图综合设计［J］.电波科学学报，2006，21（16）：16-20＋25.JIAO Yongchang，YANG Ke，CHEN Shengbing.Application of particle swarm optimization in antenna array pattern synthesis［J］.Chinese Journal of Radio Science，2006，21（16）：16-20＋25.（in Chinese）

［4］李金金，田雨波.基于量子粒子群改进算法的直线阵综合［J］.电波科学学报，2012，27（2）：255-259.LI Jinjin，TIAN Yubo.Pattern synthesis of linear antenna array based on improved quantum particle swam optimization［J］.Chinese Journal of Radio Science，2012，27（2）：255-259.（in Chinese）

［5］GIES D，RAHMAT-SAMII Y.Particle swarm optimization for reconfigurable phase-differentiated array design［J］.Microwave and Optical Technology Letters，2003，38（3）：168-175.

［6］BASKAR S，ALPHONES A，SUGANTHAN P N，Genetic-algorithm-based designed of a reconfigurable antenna array with decrete phase shifters［J］.Microwave and Optical Technology Letters，2005，45（6）：461-465.

［7］PATHAK N，MAHANTI G K，SINHA MAHAPATRA T K.Genetic algorithms for design of discrete phase-only reconfigurable array antennas with fixed dynamic range ratio［J］.International Journal Infrared and Millimeter Waves，2007，28：953-960.

［8］AKDAGLI A，GUNEY K，BABAYIGIT B.Clonal selection algorithm for design of reconfigurable antenna array with discrete phase shifters［J］.Journal of Electromagnetic Waves and Application，2007，21（2）：215-227.

［9］GUNEY K，ONAY M.Bees algorithm for design of dual-beam linear antenna arrays with digital attenuators and digital phase shifters［J］.International Journal of RF and Microwave Computer-Aided Engineering，2008，18：337-347.

［10］KENNEDY J，EBERHART R.Particle swarm optimization［C］// IEEE International Conference on Neural Networks.Perth，Australia，1995（4）：1942-1948.

［11］LING S H，IU H H，CHAN K Y，et al.Hybird particle swarm optimization with wavelet mutation and its industrial applications［J］.IEEE Transactions on Systems，2008，38（3）：743-763.

［12］高东慧，董平平，田雨波，等 .一种改进的小波变异粒子群优化算法［J］.计算机工程，2012，38（21）：145-147.GAO Donghui，DONG Pingping，TIAN Yubo，et al.，An improved particle swarm optimization algorithm with wavelet mutation［J］.Computer Engineering，2012，38（21）：145-147.