基于小波树和四叉树的图像分形编码算法研究*

牟宇飞，张文普，彭 畑，阳 溢

（重庆通信学院，重庆400035）

分形图像编码是近年来发展起来的一种编码技术，它以分形理论为数学基础[1]。BARNSLEY M于1988年首先提出基于块的编码方案[2]，分形编码就作为一种新的图像编码技术受到人们的广泛关注。随后他的学生JACQUIN A提出一个基于仿射变换的完全自动的图像编码方案[3]，分形编码的计算复杂性由值域块的匹配块的搜索过程决定。由于分形编码运算复杂度太大，编码时间过长，极大地限制了其应用。因此，缩短分形编码时间是分形编码技术面临的一个重要问题。

图像经过多级小波分解后，各级小波子带具有明显的相似性，可利用小波变换和分形编码的优势进行图像压缩编码。

小波和分形的混合编码比较经典的算法有两类：RINALDO R等人提出代表性的基于小波变换的分形预测图像编码算法[4]，低分辨率图像预测高分辨率图像的编码仍采用仿射变换，但不需收缩映射，解码时不需迭代且可直接估计均方差；DAVIS G M把零树概念引入到分形图像编码[5]，把相似块与图像块之间的分形匹配转化为相似树与图像树之间的分形匹配，通过小波变换产生子图之间的相似性，用分形方法来开发这些相似性。

1 图像小波变换和分形编码

1.1 图像小波变换

一幅图像经过小波变换后，可分解为不同方向、不同分辨率的子带图像。二维Mallat小波分解和重构算法的公式为：

多级小波变换是将上级小波变换得到的低频子带系数再进行一级小波变换。多级小波变换后将图像分解成不同分辨率的子带，如图1所示。由于图幅大小的关系，只标出了一级和二级分解的小波子带，多级小波变换产生的子带以此类推。其中，HL是水平子带，LH是垂直子带，HH是对角子带。

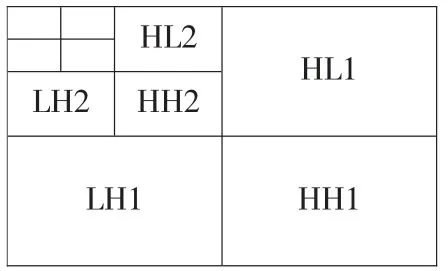
图1 小波多级分解子带示意图

小波系数的零树结构是Shaprio在研究小波系数的渐进传输时提出来的。下文中提到的小波树和零树结构有相同点，也有区别。小波树是将水平、垂直和对角3个方向上的小波子带的小波系数结合考虑，同时小波树的根可以不只是一个系数，还可以是2×2的小波系数块。

1.2 图像分形压缩编码

分形编码的主要理论基础是迭代函数系统理论、不动点定理和拼贴定理，所要解决的主要问题是把待编码的图像作为吸引子时如何得到IFS参数。基本算法的主要步骤如下：

（1）将原始图像分成不重叠的值域块（记为R块），大小为n=B×B像素。

（2）将原始图像分成可以重叠的定义域块（记为D块），大小为2B×2B像素。

（3）对每一个R块，搜索一个D块，使D块经过式（6）变换后得到的D′与R块的误差最小。R和D′的像素值分别为ai、bi（i=1，2，…，n）。

其中，γ是收缩变换，可以采取4像素取平均值得到与R块同样大小的块；Tk是8种仿射变换，包括关于x轴、y轴、y=x、y=-x对称，以及关于中心逆时针旋转0°、90°、180°和270°；I为全1矩阵，s、o、j、k为要求的参数，s为对比度因子，o为灰度偏移量，j为D块的序号，记录了D块的位置，k为仿射变换的种类。

根据最小二乘法，可以计算：

2 相关算法研究

[6]提出小波域内相邻子图的分形预测编码算法。在低分辨率子带水平、垂直和对角3个方向上分别进行分形编码，用此编码对在水平、垂直和对角3个方向上预测得到高分辨率子带的分形编码，但是没有给出具体如何预测。参考文献[7]提出对得到的低分辨率子带的分形编码进行适当的比例变换以得到高分辨率子带的分形编码，其压缩效果较好，但是获得高分辨率子带上的分形编码时，依据不是很充分，在压缩比较大时解码图像质量有所下降。参考文献[8]提出一种基于小波域的分形图像编码改进算法。该算法首先将图像分解到小波域，然后根据各子图像所包含能量的大小和所代表的方向等信息，采用不同大小、形状和类别的图像块及相似块进行分形编码。在编码过程中按照零树结构在同方向不同分辨率的各个子带图像上确定要预测的图像块，同时在同方向低一级分辨率的子带图像上寻找与其最佳分形匹配的相似块，并由各级相似块构成预测树。算法取得较高的压缩比，解码质量也有所下降。参考文献[9]提出基于方向性零树小波的分形图像编码，将小波零树与分形编码的优势相结合。

3 基于小波树和四叉树的图像分形编码算法研究

图像经过小波变换后，除去最后一级小波变换产生的4个最低分辨率子带，对其他高分辨率子带按照小波树结构形成一棵棵小波树，所形成的即为待编码的小波树，记为值域树。值域树根节点所在子带低一级分辨率子带上，也可以形成小波树结构，去掉它们在第一级小波变换的小波系数节点，则与值域树有相同的大小、相同的层次，记为定义域树。

算法的主要步骤如下：

（1）对256像素×256像素大小的灰度图像经过多级小波变换，分解成多级小波子带，如进行4级小波分解。

（2）对最低分辨率子带，也就是最后一级小波分解产生的低频子带LL4和水平HL4、垂直LH4、对角HH43个高频子带，进行失真较小的编码，采用均匀量化编码。

（3）对高分辨率子带按照小波树结构形成一棵棵小波树，即为待编码的小波树，记为值域树。小波树的根可以是单个系数，也可以是2×2的小波系数块等。设定一个阈值，当小波树的所有小波系数都小于等于阈值时直接置0，不进行分形编码。

（4）对小波系数大于阈值的值域树进行分形编码。分形编码就是搜索值域树最匹配的定义域树，搜索的范围在值域树根的位置按小波树结构对应到低一级位置邻近的一个区域，不采用全局搜索，以加快算法的速度。

令i′=ceil（i/2），j′=ceil（j/2），则i′-5≤m≤i′+5且1≤m≤16，j′-5≤n≤j′+5且1≤n≤16。

如果分形编码时误差小于等于设定的误差阈值，则记录分形参数；如果大于设定的误差阈值，则对设立标志位，对大于小波系数阈值的系数进行均匀量化编码。然后去掉根节点，对剩下的小波树结构进行分形编码，此时的定义域树也去掉根节点，如果误差小于等于设定的误差阈值，则记录分形参数；如果大于设定的误差阈值，则进行四叉树分裂，形成根节点在等4个位置上的小波树，即根节点在第2级小波子带上。此后的编码同根节点在第3级小波子带上类似。

（5）对根节点在第2级小波子带上的小波树进行分形编码，如果误差小于等于设定的误差阈值，则记录分形参数；如果大于设定的误差阈值，则设立标志位，对大于小波系数阈值的系数进行均匀量化编码。

编码算法流程图如图2所示。

解码是编码的逆过程，由LL4、HL4、LH4、HH4逐级外推解码出3级、2级、1级小波子带，最后进行多级小波重构，恢复出原图像。

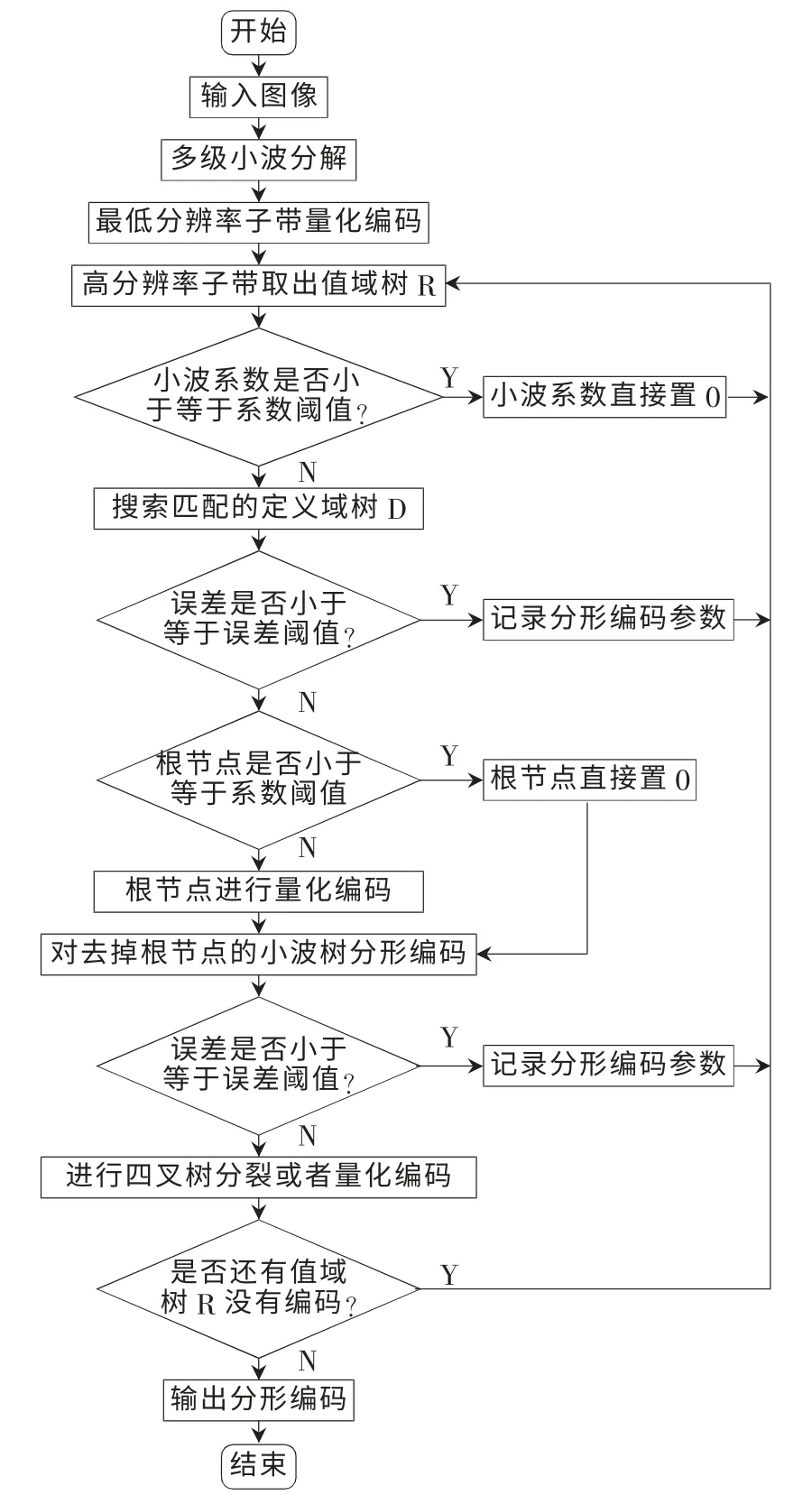
图2 编程算法流程图

4 实验结果与分析

对Lena、cameraman和couple 3幅256×256的标准测试灰度图像进行了分形编码解码实验，实验环境为Core i3 M330 CPU，2GB内存，Windows XP系统。用Matlab进行仿真实验，并将基本算法、参考文献[8]算法与本文算法进行了比较。

实验1

分别用上述3种方法对标准测试图像Lena进行分形编码解码，结果如图3所示。可以看出本文算法还存在一定的块效应，这是由于对某些小波系数直接置0所引起的。

实验2

对标准的测试图像cameraman进行分形编码解码，结果如图4所示。可以看出本文算法存在块效应，同时人物的手部不是很清晰，还有改进的余地。

实验3

对标准的测试图像couple进行分形编码解码，结果如图5所示。

图3 实验1结果

图4 实验2结果

图5 实验3结果

最后列出了各算法的编码时间、PSNR和压缩比，如表1所示。

从表1可以看出，与基本算法相比，本文算法在解码图像质量上，Lena图像在根采用单节点时PSNR略有提高，在根采用2×2块时略有下降；couple图像的PSNR值略微下降；cameraman图像在根采用单节点时PSNR值提高了约1.8 dB，在根采用2×2块时也提高了1.1 dB。与参考文献[8]算法相比，3幅图像的PSNR值都有很大提高，平均提高了5 dB。但是本文算法在一些图像细节边缘上不够清晰，存在一定的块效应，还有待改进，如考虑减小阈值或者设置感兴趣区域。

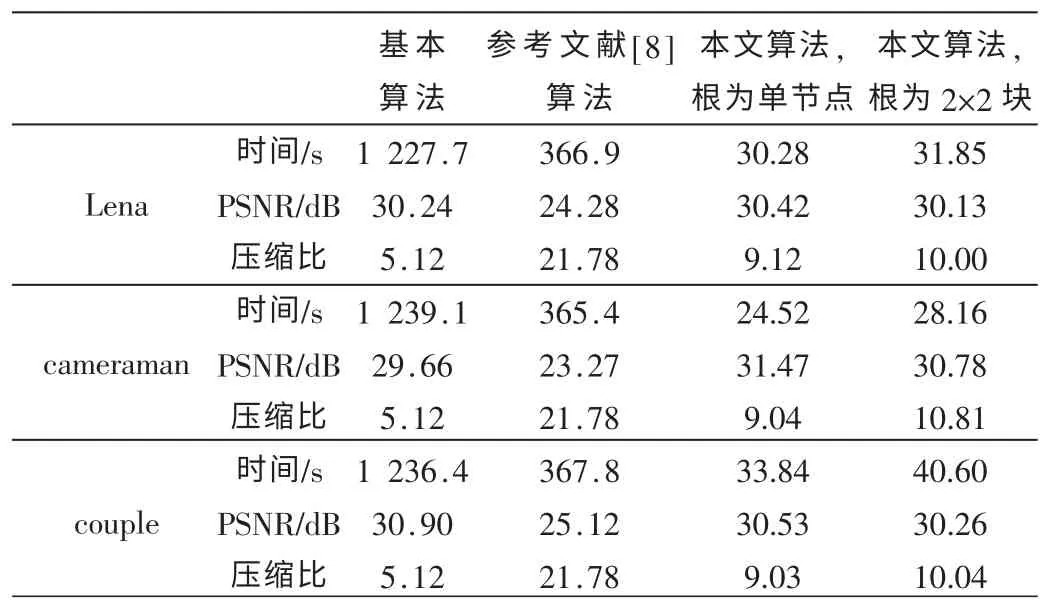
表1 实验结果比较

由于搜索匹配树是在值域树相应的邻近区域搜索，没有采用全局搜索，且没有进行8种仿射变换，运算速度有很大改善，运算时间大约为基本算法的1/40，为参考文献[8]算法的1/12。

从压缩比来看，参考文献[8]算法最高，本文算法次之，基本算法最低。对本文算法，根采用2×2块时与根采用单节点相比，在解码图像略微降低的情况下，提高了压缩比。

将小波变换与分形编码相结合对图像进行压缩编码，发挥两者的优势是值得研究的方向。小波分解形成3个方向的子带，自然地对分形编码中的定义域块和值域块进行了分类，从而减少了编码搜索的时间。同时，小波分解产生的各级子带间具有较强的相似性，分形的优势正好在于自相似性强的图像，如何利用分形开采这种相似性，提高图像解码质量，有待于深入地研究。

参考文献

[1]夏良正，李久贤.数字图像处理（第2版）[M].南京：东南大学出版社，2006.

[2]BARNSLEY M.Fractal everywhere[M].San Diego，CA：Academic Press，1988.

[3]JACQUIN A.A Fractal theory of iterated markov operators with application to digital image coding[D].Atlanta：Georgia Institute of Technology，1989.

[4]RINALDO R，CALVAGNO G.Image coding by block prediction of multiresolution subimages[J].IEEE Transactions on Image Processing，1995，4（7）：909-920.

[5]DAVIS G M.A wavelet-based analysis of fractal image compression[J].IEEE Transactions on Image Processing，1998，7（2）：141-154

[6]谢永华，傅德胜，任卫华.一种基于小波变换的图象分形编码压缩算法的研究[J].中国图象图形学报，2003，8（7）：839-842.

[7]张梁斌，奚李峰.一种基于小波域的分形编码预测方法[J].计算机应用与软件，2007，24（6）：68-70.

[8]娄莉.一种基于小波域的分形图像编码改进算法[J].计算机技术与应用，2010（7）：134-136.

[9]张宗念，马义德，余英林.基于方向性零树小波的分形图像编码[J].电子科学学刊，2000，22（5）：780-784.