数字相移测量中的高精度相位误差补偿＊

褚利文，张 旭，朱利民

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海大学 机电工程与自动化学院，上海 200072）

引 言

相位轮廓术（phase measurement profilometry，PMP）是一种以相移为基础的结构光测量方法，它能够很好地抑制被测对象表面的颜色、反射率以及环境光的干扰［1］。通过分析多幅有一定相位差的光栅条纹图像，PMP能够计算图像中像素的相位值，进而求解出观察点的深度信息［2－3］。投影机和摄像机的非线性所导致的γ 畸变是数字PMP测量的主要误差来源［4－11］。Huang P S［4－8］等学者都先后从不同角度对γ畸变模型进行了深入研究，得出γ畸变引入的高次谐波项是相位误差的主要来源，因此相位误差具有一定的规律［8］。Huang P S［9－11］等提出了多种办法补偿相位误差。

γ校正法和相位误差补偿法能够有效提高相位精度，但均忽略了γ非均匀分布的多特点，仅采用单一γ对整个图像进行校正而导致的参与误差在高精度检测应用场景中是无法忽略的。文章对数字投影机的亮度非均匀分布和γ非均匀分布的规律进行研究，通过理论分析和实验验证相位残余误差，提出一种基于像素的相位误差查找表，根据γ的分布规律进行相位误差补偿，有效提高了相位精度并最大限度优化了算法的空间和时间效率。

1 相移原理

在相移法中，相移条图案中的任意点亮度可表示为：

其中，x 为横 坐 标，In为 亮 度，A 和B 均 为 常 数，f 为 正 弦 曲 线 的 频 率，n 为 当 前 相 移 步 数，N 为 相 移 总 步数。在不考虑γ的情况下，该点在摄像机拍摄到的图像中对应点的亮度为：

其中，A′为该像素在各步相移中亮度的平均值，可以表示为：

该点亮度在相移过程中的变化量可表示为：

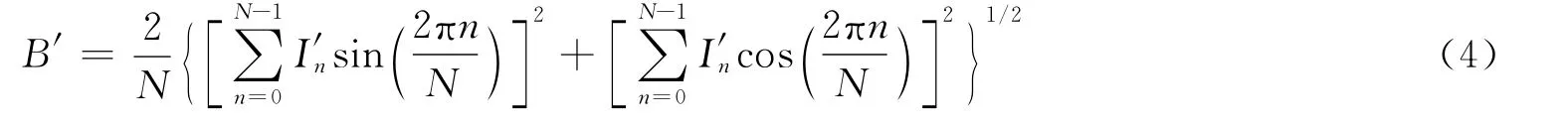
该像素的相位值φ 可表示为：

2 γ畸变

结构光测量系统中的亮度传递函数是非线性的，系统投射出的正弦条纹图案包含了高次谐波项。如图1所示，其中二次、三次谐波项都由γ畸变导致的。γ畸变导致的相位误差，如图2所示。

3 投影机的γ非均匀性

数字投影机的投影范围某一点的实际输出亮度与位置有关。图3所示为不同位置点的亮度传递函数，可表示为：

任意点的γ可以表示为：

图1 γ畸变正弦曲线及频谱分析Fig.1 γdistorted sinusoidal curves and frequency analysis

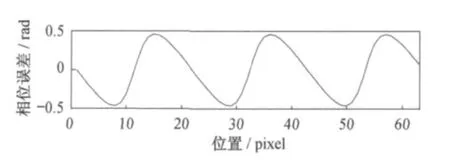
图2 γ为3.3时的相位误差Fig.2 Phase error whenγis 3.3

图3 不同点的亮度传递函数对比Fig.3 Comparison of intensity response curve at different points

因此可以得出如下关系［8］：

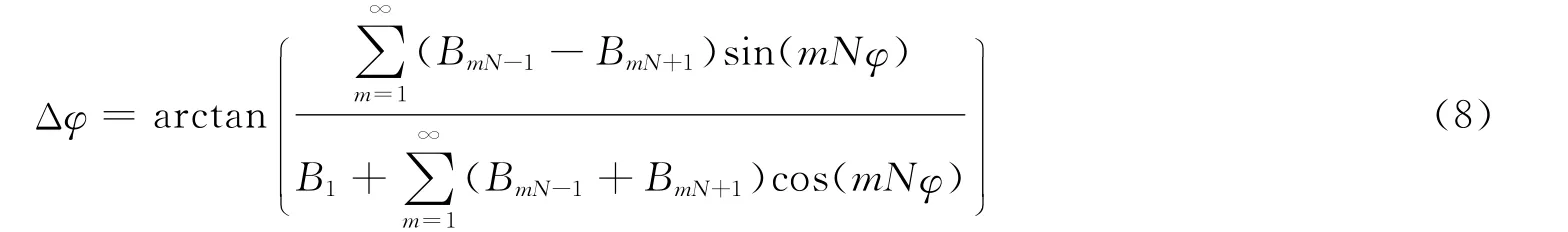
其中

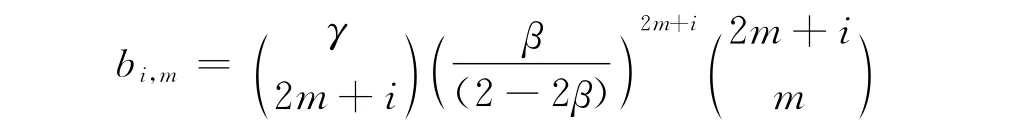
当γ在1～5之间时，γ与最大相位误差之间的关系如图4所示。

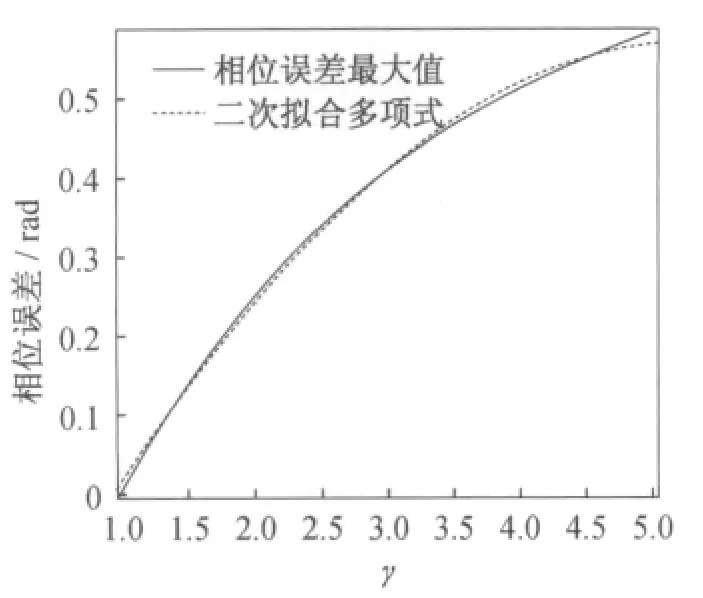
图4 相位误差最大值与γ的关系Fig.4 Relationship betweenγand maximum phase error

图5 亮度输入输出指数拟合Fig.5 Curve fitting of intensity response using power function

γ和最大误差的关系可拟合为：

对式（9）两边同时求一阶导数：

由式（10）得出，当γ变化0.01时，最大相位误差改变了0.003 2。该误差对于高精度测量是不能忽略的。事实上，γ服从正态分布［8］，并且标准差大于0.02。因此γ的非均匀分布特性在进行相位误差补偿时必须加以考虑。

4 相位误差校正

γ可以通过以下方法进行标定［10］：首先调节投影机至聚焦状态，然后向标准白板投射白光，亮度从0～255依次递增。根据γ所服从的幂律定律，由式（6）和式（7）可得式（11），任意点的亮度输入输出关系都服从式（12）的关系函数，并且该点的γ＝g（x，y），进而得到γ矩阵Gm×n。其中，m 和n 分别为图像的宽和高。

根据γ矩阵，可以在相位误差查找表（look up table，LUT）［11］的基础上，基于单个像素建立二维相位误差查找表：

第一步：在γ 的最大值和最小值之间取均匀间隔d，根据γ 标定实验结果的有效数字，间隔d＝0.01时能够获得较高精度。

第二步：用查找表存储理论相位与实际相位之间的相位差。

第三步：将相位误差查找表与相应的γ关联起来，并存储在查找表中，见图6（a）。

测量中对任意点都可以使用相位误差查找表进行相位误差补偿。首先根据γ 矩阵确定该点的γ＝G（x，y）；其次根据γ确定相应的相位误差查找表，对介于表中两个值之间的γ可通过线性插值来计算出相应的相位误差查找表，见图6（b）；最后进行相位误差补偿。

对于特定的系统，只需事先进行一次标定便可建立基于像素的相位误差查找表，不会影响实际测量过程。任意γ对应的相位误差查找表通过线性插值动态生成，具有良好空间效率和时间效率。

图6 基于像素的相位误差查找表及插值方法Fig.6 Pixel based phase error look－up table and interpolation method

5 实验与分析

通过标准白板和复杂自由曲面对象测量实验进一步验证了方法的有效性，并将结果与现有方法进行对比。图7为实验系统设备。实验使用的结构光测量系统由一台联想T160DLP投影机（分辨率1 024×768）和一个Adimec 1000c（分辨率1 024×1 024）工业相机组成，见图7（a）。图7（b）和图7（c）分别为实验用标准白板和复杂曲面对象。

图7 实验系统设备Fig.7 Measuring system and devices

图8 所示为系统标定所得的伽玛矩阵。γ 的分布具有明显的区域性和非线性。图中γ 的平均值为3.44 ，标准差为0.04。

通过以下3种方法分别对标准白板进行测量并获得相位值：

（1）单一γ校正技术［8－9］；

（2）基于固定相位误差查找表的相位误差补偿［11］；（3）基于像素相位误差查找的相位误差补偿。

对三组结果分别选取第100行、450行和800行进行横截面相位分析，每个横截面选取650个数据点，实验结果如表1所示。第一列为单一γ 校正技术结果，存在明显的残余误差；第二列为固定相位查找表补偿结果，图像中心区域的第450行补偿效果良好；但位于图像边缘处的第100行和第800行仍存在明显残余误差；第三列为基于像素的相位误差查找表补偿结果，整个图像区域内具有良好的补偿效果。与前两列相比，相位误差的均值和标准差分别减小了25%和10%，说明该方法能够有效地提高相位误差补偿的精度。

图8 γ分布图Fig.8 γdistribution

对于表面复杂白色石膏雕像同样依次进行了上述三组实验，并且在此基础上进行了相位解卷绕与三维曲面重构，结果如图9所示。图9（a）只进行γ 校正，曲面仍存在水波纹；图9（b）进行线性表校正后，中心区域的水波纹得到了明显的抑制，但是边缘区域仍不够光滑；图9（c）进行了基于像素的相位误差表校正，图整个区域内都得到了光滑的曲面，有效提高了曲面质量。

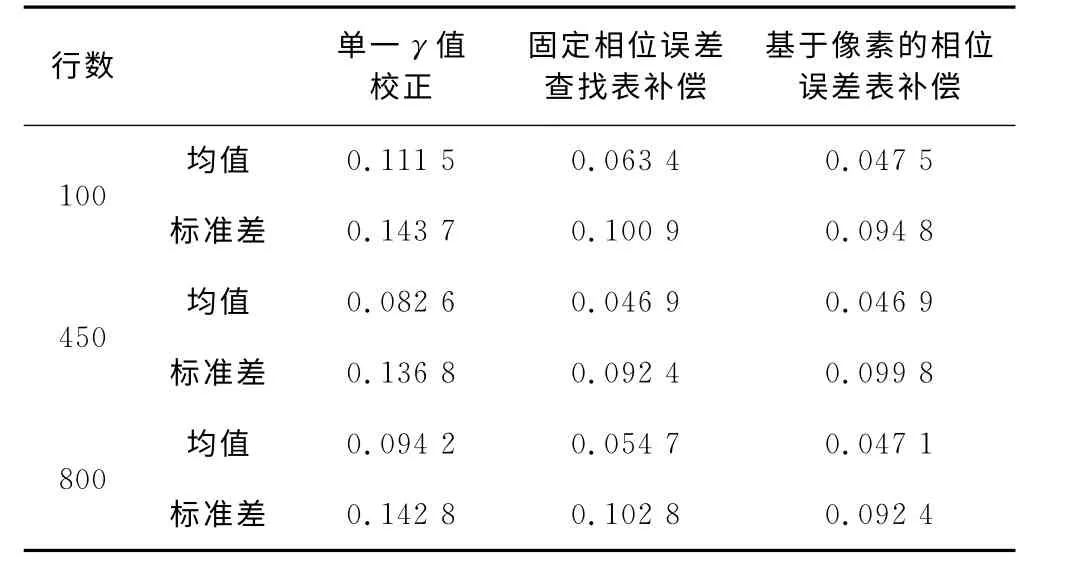
表1 标准白板实验结果Tab.1 Standard white board experiment results

图9 复杂曲面对象实验Fig.9 Complex surface object experiment results

6 结 论

γ畸变导致相移条纹包含高次谐波项，条纹实际亮度变化呈非正弦化，计算求解出的相位结果包含相位误差。针对数字投影机结构特点，通过实验分析研究数字投影机亮度值和γ值非均匀分布的特性，推导出γ波动产生的相位误差波动，指出测量结果中的残余误差对于高精度测量是无法忽略的。在此基础上，通过标定得出γ矩阵，提出了基于像素的二维相位误差查找表，改进了基于单一γ的查找表补偿方法相位测量。通过多组实验，对比了现有校正方法及文中提出的方法。实验结果表明，提出的方法比现有校正方法误差减小了。

［1］ GORTHI S S，RASTOGI P.Fringe projection techniques：whither we are？［J］.Optics and Lasers in Engineering，2010，48（2）：133－140.

［2］ SRINIVASAN V，LIU H C，HALIOUA M.Automated phase－measuring profilometry of 3－D diffuse objects［J］.Applied Optics，1984，23（18）：3105－3108.

［3］ ZHANG S.Recent progresses on real－time 3Dshape measurement using digital fringe projection techniques［J］.Optics and Lasers in Engineering，2010，48（2）：149－158.

［4］ HUANG P S，ZHANG C P，CHIANG F P.High－speed 3－D shape measurement based on digital fringe projection［J］.Optical Engineering，2003，42（1）：163－168.

［5］ GUO H W，HE H T，CHEN M Y.Gamma correction for digital fringe projection profilometry［J］.Applied Optics，2004，43（14）：2906－2914.

［6］ HOANG T，PAN B，NGUYEN D，et al.Generic gamma correction for accuracy enhancement in fringe－projection profilometry［J］.Optics Letters，2010，35（12）：1992－1994.

［7］ 郑东亮，达飞鹏，提高数字光栅投影测量系统精度的Gamma校正技术［J］.光学学报，2011，31（5）：1－6.

［8］ LIU K，WANG Y C，LAU D L，et al.Gamma model and its analysis for phase measuring profilometry［J］.JOSA A，2010，27（3）：553－562.

［9］ HUANG P S，HU Q J，CHIANG F P.Double three－step phase－shifting algorithm［J］.Applied Optics，2002，41（22）：4503－4509.

［10］ ZHANG S，HUANG P S.Phase error compensation for a 3－D shape measurement system based on the phase－shifting method［J］.Optical Engineering，2007，46（6）：0636001－0636019.

［11］ ZHANG S，YAU S T.Generic non－sinusoidal phase error correction for three－dimensional shape measurement using a digital video projector［J］.Applied Optics，2007，46（1）：36－43.