五路环形交叉口交通量观测及计算方法研究＊

（武汉理工大学交通学院 武汉 430063）

0 引 言

交叉口是城市道路的节点，是城市交通网络的瓶颈位置，因而交叉口的通行能力能否满足高峰时段交通流量的需求是反应该地段是否拥堵的重要因素．调查得到的交叉口各个方向的流量数据及对其处理准确与否，将直接影响交叉口通行能力的计算分析，进而影响整个城市的规划布局，因此，对交叉口交通流量的计算方法进行研究的重要性是不言而喻［1］．

对于3路或4路环形交叉口，通过实际交通调查得到的进口交通量、出口交通量、进口右转交通量以及交织断面的交通量4种基础数据就可计算出各进口流向交通量［2－3］，但该方法并不适用于5路环形交叉口．5路环形交叉口流向数量的增多加大了计算交叉口流向分布的难度．马健霄利用不同颜色的卡片对部分进口道的车流进行随机抽样，以样本分析结果推算实际结果，设计了针对5路环形交叉口交通量的卡片调查法［4］，但该方法应用在交通量较大的环形交叉口时获得的理论值与实际值误差较大．以上方法均是将人工观测法与数学理论相结合，只要人力、物力和财力充足，计算出的各流向交通量与实际交通量误差较小．钱红波，况爱武等应用双约束重力法对五路环形交叉口的流向分布进行了预测［5］．于春青、程琳运用线性方程法对4路环形交叉口的流向分布进行了预测，但这2种方法预测的准确性作者均未作相应讨论．本文将以上2种方法应用于5路环形交叉口，将各进口流向预测交通量与实际交通量对比分别确定其适用性和精度．

1 五路环形交叉口

一般来说，城市内外交通衔接区域交通构成复杂，该区域的相交道路数目较多，易形成多路环形交叉的情况．这一结论与实际是极其相符的，有调查统计数据显示大多数的5路环形交叉口一般位于城市交通咽喉［6］．因此如果该类型的交叉口处理不妥当，对城市交通的畅通性将会产生非常重大的影响．

根据交通工程学的定义，5路环形交叉口属于复合型交叉口，此类交叉口的交通组织比较复杂．其每个进口道的车流有4个流向，总共20个流向，即使能够在进口道处直接观测出右转的车流量，依然需要求解剩下的15个流向的车流量，但交织断面调查法只能观测到10个进出口的总交通量，和5个交织断面的交通量，不能求出各个流向的交通量．因此无法通过观测直接求出各个转向的车流量．

车辆在进入环形交叉口后按同一方向绕岛行驶，车辆间的状态分为分流、合流和交织．假设在环岛上车程最大的车辆只行驶在内行车道上，车程最小的车辆只行驶在外行车道上，其他车辆只在中间行车道行驶，且进环之后不准换道．车流在无控交叉口环道行驶过程中共有2类冲突点，分别为同一环道上的交织冲突点和不同环道上的交叉冲突点［7］．5路环交的交织冲突点有15个，交叉冲突点有30个，一共为45个冲突点，见图1．

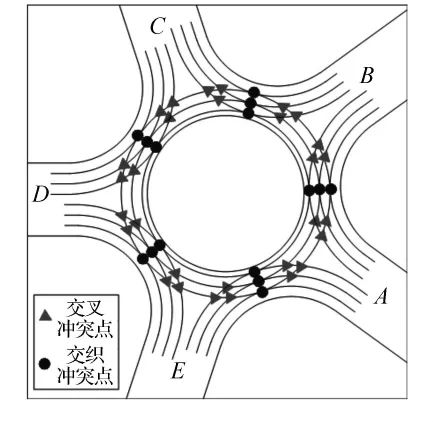
图1 交叉口冲突点示意图

采用交通枢纽复杂性指标A来评价交叉口的复杂程度

式中：A为交通枢纽复杂性指标；nw为交织冲突点，权重系数为1；nc为交叉冲突点，权重系数为3．

线性加权叠加后，算得交叉口复杂度A＝105．

计算环形交叉口的各流向流量要针对不同的情况采取不同的方法，其复杂程度与交叉口的进口道数成正比．5路环形交叉口是较复杂的一类交叉口，其各路流量的算法也不同于4路或3路环形交叉口．目前，较多用的环形交叉口各路流量算法有线性方程组法和双约束重力模型法，下面分别对这2种方法的模型及其使用范围做进一步的分析．

2 环形交叉口各流向流量计算方法研究

对于大型环形交叉口或环岛中心有建筑物等障碍视线的环形交叉口，无法直接观测到转向车辆的种类和流量，这时就无法采用通常的交叉口交通量调查计算办法来进行流量调查．因此，需通过观测进出环交的流量、右转流量以及交织区流量来计算和检验结果．

2.1 五路环形交叉口交通量调查

本次研究设计交通量调查方案中，需观测交叉口各路进出流量、交织区流量和右转流量，各流量及调查人员站位见图2．

图2 调查交通量和调查员站位示意图

图中A路，IA为进口车辆数，OA为出口车辆数，TAB为通过AB2路段交织处车辆数，以及IAB为由A路右转至B路的车辆数，其他B，C，D，E路符号含义类推．一般而言，交通流量调查会选择最不利的情况下进行，即出行的早晚高峰时段，这样更能反映出现状道路网络的结症之处［8］．因此，在做五路环形交叉口流量调查时，选择观测环形交叉口在早、晚高峰时段各2h的流量作为调查的交通流量．同时在对各进出口流量进行统计分析之前，需将各类车辆的交通量换算为标准小客车交通量，各种类型车辆的折算系数见表1．

表1 各种不同类型车辆折算系数

在实际环形交叉口流量调查中，由于调查时会存在一定的误差，驶入交叉口的交通流量之和可能并不等于驶出交叉口的交通流量之和．为了确保调查时段内进出交叉口的流量平衡，必须对调查数据进行一定的预处理．比如将进出口流量两者之间的差值平均地分摊到较小的那个数据上，确保交叉口进出流量保持一致．

2.2 线性方程组法

2．2．1 构造模型 根据交通量观测，假设在A路，进口车辆数IA，出口车辆数OA，通过AB两路段交织处车辆数TAB，以及由A路右转至B路的车辆数IAB，B，C，D，E路同理．见图3．

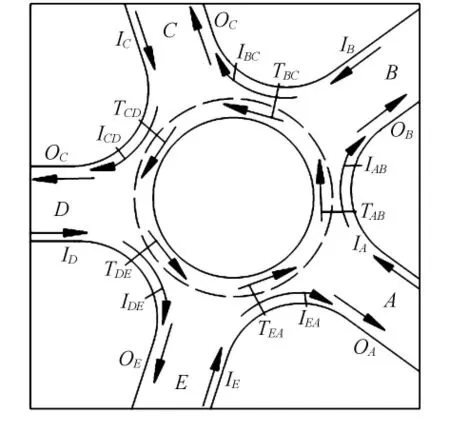
图3 5路环交流量示意图

式中：Tij为由i路口进从j路口出的交通量；Iij为由i路口右转至j路口的交通量；Ii为i路口的进口交通量；Oi为i路口的出口交通量．其中i，j分别为A，B，C，D，E．

2．2．2 具体算法 将式（2）～（4）写成矩阵形式，即将方程组转化为Ax＝b形式．

然后用MATLAB对方程组求解，并满足条件IA＋IB＋IC＋ID＋IE＝OA＋OB＋OC＋OD＋OE．若矩阵的秩不能满足rank（A）＝rank（A／b），则需用x＝A／b除法求解．

从构造线性方程组法模型来看，其思路简单直观，操作便捷，且方程本身已诠释了各路口的车流量分配方法．但是对于5路环形交叉口，方程求解时有一定的难度，尤其是在由普通方程转化为矩阵形式时较复杂，而且对调查数据要求较多、精确程度要求也较高．因此该方法较适合于少于五路的环形交叉口．

2.3 双约束重力模型法

重力模型法预测出行分布考虑了2个交通小区的吸引强度和它们之间的阻力，认为2个交通小区的出行吸引与2个交通小区的出行发生量与吸引量成正比，而与交通小区之间的交通阻抗成反比［9－11］．

2．3．1 构建模型 对于5路环形交叉口，无法直接观测出各流向的交通流量，但可以利用交通分布预测的重力模型法进行流量流向分析．假设交叉口的进口相当于出行起点，交叉口出口相当于出行终点，则进口流量相当于出行生成量，出口流量相当于出行吸引量，那么利用交叉口进出口流量计算交叉口各流向流量的问题就转化为已知交通发生量和吸引量求交通分布的问题，即交通分布预测．在环形交叉口中，假设从第i路口进从第j路口出交叉口的流量Tij与调查时段内第i路口进入交叉口的交通量Ii和第j路口离开交叉口的交通量Oj的乘积成正比，但与距离无关（因为各路口之间的交通流向与它们之间的距离无关）．交叉口的回头车的比例一般较小，可以近似地假设为零，如果遇到掉头车辆数较大的路口，可以通过调查确定掉头车辆的比例，在进行流量分析时直接将其扣除，从而构造一个虚拟的交通阻抗矩阵Rij，矩阵对角线的元素为无穷大，其他元素全部为1．为了保证必须同时引进行约束系数ki和列约束系数，构造双约束重力模型

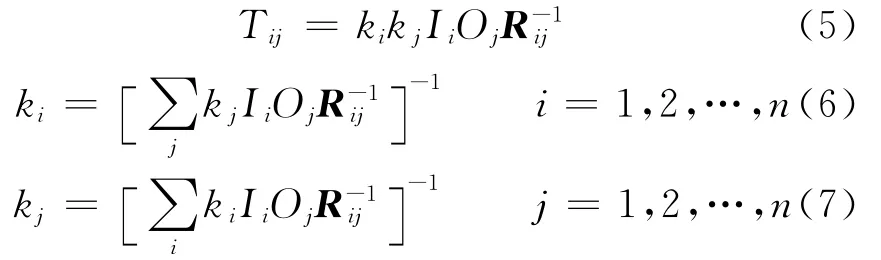
式中：ki，kj分别为行约束系数和列约束系数；Rij为i路口到j路口的交通阻抗矩阵．

2．3．2 具体算法

步骤1 首先令各个列约束系数ki＝1（i＝1，2，…，n）．

步骤2 将各列约束系数kj＝1（j＝1，2，…，n）代入式（6）求各个行约束系数ki．

步骤3 再将求得的各个行约束系数ki（i＝1，2，…，n）代入式（7）中求各个列约束系数kj．

步骤4 比较前后两批列约束系数，考察其相对误差是否小于3%，若是，转至步骤5，否则转至步骤2．

步骤5 将求得的约束系数ki，kj代入式（5）求环形交叉口各路口的车流流向，算法结束．

由双约束重力模型可以看出，只需调查进出口断面通过的车流量即可计算出交叉口各方向的车流量情况．因此，双约束重力法需要调查的数据较少，减轻了调查强度．同时对调查数据精度要求较低，通过多次迭代能够计算出较合理的流量结果．适用于五路或多于五路的环形交叉口各流向流量计算．

3 实例研究

在台州中心大道环形交叉口进行调查，测得五路进出口以及交织段车流量．根据进出口平衡原则，进口多出的流量分摊到各出口中去．通过折算得到标准车流量，见表2、表3．

表2 早高峰各路口进出车流量调查数据 pcu／h

表3 交织段、右转流量调查数据 pcu／h

采用线性方程组法，代入数据得到一个15×15矩阵．基于最小二乘法利用Matlab软件编程对方程求解，得出解为负值或不存在，说明调查数据与真实流量存在较大偏差，致使方程组出现病态．

而在相同的调查数据基础上，采用双约束重力法来确定各路口流量流向，情况却得到明显的改善．经过叠代，得到各路口流量流向，见表4．

表4 早高峰运算结果 pcu／h

4 结束语

本文介绍了2种计算环形交叉口各路交通流量的计算方法，即线性方程组法和双约束重力模型法，并在比较两种方法的基础上分别提出了每种方法的适用范围．线性方程组法要求调查的数据较多，调查工作量繁重，数据处理过程复杂并且求解难度较大，实际上精度也不高；而重力模型法只需各进出口的流量相关数据，对调查数据要求较少，资源占用少，数据处理及求解过程较简单，而且精度满足需求．在调查人力不足时双约束重力模型法更实用．通过实例分析比较得出，对于五路环形交叉口，当在调查数据有误差甚至错误的情况下，通过双约束重力模型法可以获得较准确的流向流量结果．因此，线性方程组法只适合相交道路数在5路以下有准确交通量观测数据的环形交叉口流量计算，双约束重力模型法较之则具有更广宽泛的适用性、更高的精度和更好的实用性．

［1］徐良杰，城市交叉口交通量调查方法研究［J］．交通与计算机，2003，21（4）：6－9．

［2］于春青，程 琳．环形交叉口的流量测定方法探讨［J］．交通标准化，2006（10）：55－58．

［3］Transportation Research Board．Highway capacity manual（HCM），Special report209，TRB，National research couneil［G］．Washington D．C．：Transportation Research Board，1985．

［4］仲小飞．五路环形交叉口交通量卡片调查法［J］．城市交通，2009，7（6）：71－75．

［5］钱红波，况爱武，何显慈．基于双约束重力模型的环形交叉口流量流向分析［J］．长沙交通学院学报，2004，20（3）：74－76．

［6］张卫华，王召阳，张胜凯．五路交叉口交通改善方法及其应用［J］．交通科技，2011（1）：96－99．

［7］杨锦冬，杨晓光．环形交叉口交通控制模式研究［J］．公路交通科技，2000，17（3）：48－51．

［8］杨晓芳，王建蓉，牛兆雨．五路环形交叉口瓶颈控制方法［J］．公路交通科技，2012，29（8）：99－105．

［9］樊立军．环形平面交叉口设计理论的发展及其在我国的应用［J］．民营科技，2007（3）：115－116．

［10］THAI M J．The design of roundabouts in France：Historical context and state of the art．［M］．TRB．Washingdon D．C．，2000．

［11］李安勋．基于运营组织的城市群轨道客流预测方法研究［D］．武汉：武汉理工大学，2007．

Study on Methods of Traffic Volume Observation and Calculation at Five－leg Roundabout

YAO Yihu XU Liangjie QIN Yaxiao
（School of Transportation ，Wuhan University of Technology ，Wuhan 430063，China）