基于遗传算法的数控喷字路径优化方法研究＊

周 盛 李 瑞 汪 洋

（武汉理工大学能源与动力学院1） 武汉 430063） （大连理工大学船舶工程学院2） 大连 116024）

（大连中远船坞工程有限公司3） 大连 116113）

在船体建造过程中，钢料划线和切割主要由数控切割机来完成，但是在大多数船厂中，在切割零件上标注零件编号、装配符号等施工信息时仍由手工完成，效率较低，有的船厂采用数控喷字设备来完成钢板上零件的喷字标注，相对于人工标注，数控喷字设备的使用提高了喷字效率，但是，零件的喷字顺序往往人为给定，容易造成数控喷头空行路径过长，因此，为了减少喷头空走路径，提高设备的效率，本文根据钢板上喷字的坐标位置和字符长度，对喷头行走路径进行了优化研究．

旅行商问题（traveling salesman problem，TSP）是计算机科学中的一个典型问题［1］，本文将数控喷字路径优化问题与旅行商问题进行了对比分析，将旅行商问题中节点间路径的优化扩展为数控喷字路径中有向线段间路径的优化，在此基础上，建立了数控喷字路径优化数学模型，并采用遗传算法对其进行了求解．

1 问题描述与分析

1.1 TSP问题描述［2－3］

旅行商路径问题可描述为：已知n个城市各城市间的距离，某一旅行商从某个城市出发访问每个城市一次且仅一次，最后回到出发城市，怎样安排才使其所走路线最短．

其数学模型为：对于城市ti的一个访问顺序为T＝（t1，t2，…，tn），则旅行商问题为求商人所行的最短路径，即为

式中：Ω为n个城市不重复排列的所有可能的回路．因此，旅行商问题实际上即是给定的一组离散点，求不重复连接所有离散点的最短路径．

1.2 数控喷字路径数学模型

数控喷字路径优化与旅行商问题类似，可以抽象为求不重复连接所有字符串的最短路径，二者的区别是旅行商问题是基于一组离散点，每个离散点的特征属性仅是点坐标；数控喷字路径优化问题是基于一组字符串，每个字符串的特征属性根据数控喷字的指令文件有起始点坐标、字符串与X轴角度和字符串长度，因此，可以将每个字符串看成是一条有向线段，数控喷字路径优化问题再次抽象为求不重复连接所有有向线段的最短路径，见图1a）是给定的一组有向线段，见图1b）是这一组有向线段的路径图．数控喷字路径的优化就是确定这组有向线段的顺序，使得喷头按这一顺序所行的空行路径最短．

图1 喷字路径示意图

1.3 喷字路径优化分析

根据上述对数控喷字路径优化问题的描述及其数学模型的建立，从中可以发现其问题的求解思路、方法与求解TSP问题有相似之处．通过把数控喷字优化问题与TSP问题进行对比分析可知，它们都是一个如何合理安排路径的问题，所以可以把喷字路径优化问题归结为特殊的TSP问题进行求解．

数控喷字路径优化在TSP问题下可以描述为：对于一组待喷字符段，数控喷头首先从原点（未启动的停放位置）开始，在工作台平面上沿着使总空行路径最短的轨迹，空走移动到待喷字符段的起始点上，然后按照数控程序指令进行喷字，喷完该段标注字符后，再移动到其他的喷字字符段重复该喷字过程．直到所有喷字字符段都喷完，然后喷头回到原点位置．

因此，可以根据每个字符串的起始点坐标、与X轴的角度和字符串长度，求出每个字符串的终点坐标，这样，就可以将数控喷字路径优化问题转化为一一对应的一组起始点和终点的TSP问题，增加约束条件为：数控喷头行走到一个起始点后，下一步只能行走到与其对应的终点位置，再下一步的路径，只能以剩下的起始点为目标，以此类推．优化目标即是使数控喷头的空行程最短．

2 遗传算法求解特殊TSP问题

遗传算法是一种搜索最优解的方法［4－6］，该方法是通过模拟生物进化过程实现的．遗传算法以群体中的所有个体为对象，对解空间的每一个个体进行编码，通过遗传操作选择、交叉、变异等迭代从解空间寻找含有最优解或较优解的组合．在进行个体优劣的判断时，利用由目标函数构造的适应度函数来进行判断．通过对每一代群体都进行遗传迭代操作，那么解空间中的解就向最优解逼近，到遗传算法终止，则所得可行解即为最接近最优解的解．

1）编码 本文使用路径顺序表达形式．这种表达方法是TSP问题的最自然、最简单的表示方法．例如：对于一个有9个喷字字符段的的待加工零件，其喷字顺序为1－3－2－5－4－7－6－9－8可简单表示为［1 3 2 5 4 7 6 9 8］，表示从1号字符段出发依次经过3，2，5，4，7，6，9，8字符段最后返回1号字符段的一条路径．并且这种表达方式满足TSP问题的约束条件．保证了每个字符段经过且只经过一次．

2）生成初始群体 种群规模越大，种群的多样性越好，算法越容易跳出局部最优．但随着种群规模的增大，计算量增大，算法易产生早熟，一般都是随机生成规模为N的初始群体，N的值取为20～200．

3）适应度函数 对于求解最小值问题，采用如下变换

式中：cmax为一个适当大的数．cmax取为群体中最差个体的路径长度，就相当于差个体淘汰制．

4）确定交叉算子 目前己有多种交叉算子，如部分映射交叉算子，序交叉算子、循环交叉算子，其中启发式交叉和边重组交叉相对有效．本文选用启发式交叉算子．

3 数控喷字路径优化实例

应用Matlab编写基于遗传算法的数控喷字路径优化程序，以某块船体外板上30个喷字字符段为例，首先确定以下参数如下：种群大小N＝30；最大进化代数T＝100；交叉概率Pc＝0．65；变异概率Pm＝0．01；赌轮盘选择算子；启发式交叉算子；变异算子．

经过遗传算法50代后的结果就得到了较大的改进，已开始在接近最优近似解．在60代之后两代中最好解之间的误差不超过5%，为了在更短的时间内得到较满意的解，即可在60代时终止遗传进化．这在连续处理较多数量钢板的喷字路径优化时，时间上的优势会比较明显．

对于未集成路径优化算法的喷字设备，其原始喷字路径图见图2，图3是采用遗传算法路径优化计算结果的路径图．优化后空行路径比未优化的路径减少了22%．

图2 原始路径图

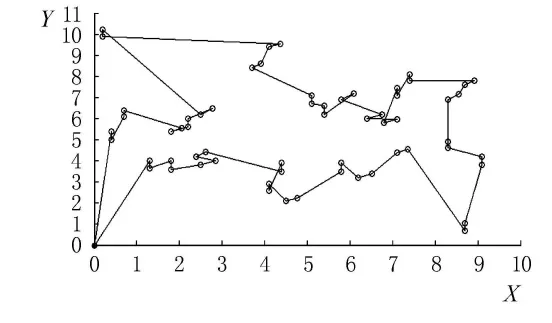
图3 遗传算法优化后路径图

4 结束语

将数控喷字路径优化问题与计算科学中经典的TSP问题进行了对比分析，根据喷字特征，将喷字字符串抽象为有向线段，因此，将数控喷字路径优化问题抽象为一一对应的一组起始点和终点的特殊的TSP问题，建立了数控喷字路径优化的有向线段路径优化模型，以喷字空行路径最短为目标，利用遗传算法进行了求解．

通过实例计算结果表明，基于遗传算法的数控喷字路径优化方法，能够大幅减少数控喷头的空行路径，由此提高数控喷字设备的加工效率．

［1］邢文训，谢金星．现代优化计算方法［M］．北京：清华大学出版社，1999．

［2］ALBERTO G，RICARDO G．A particale swarm－based met heuristic to solve the traveling salesman problem［C］／／Procedings of the 2006International Conference on Artificial Intelligence，2006：698－702．

［3］HANG，NA S．A study on torch path planning in laser cutting process，part 2：cutting path optimization using simulated annealing［J］．Journal of Manufacturing Process，1999（1）：62－70．

［4］孙惠文．遗传算法求解旅行商问题［J］．西南交通大学学报，1996，31（5）：550－554．

［5］喻 菡．遗传算法求解TSP的研究［D］．成都：西南交通大学，2006．

［6］GREFENSTETTE J，COPAL R，ROSIMAITA B．Genetic algorithms for the traveling salesman problem［C］／／Proc Int Genetic Algorithms and Their Applications Conference，1985：160－168．