基于Delaunay三角网的跨比例尺点要素综合算法

柳华桥，舒宾，周义军

(天津市测绘院，天津 300381)

基于Delaunay三角网的跨比例尺点要素综合算法

柳华桥∗，舒宾，周义军

(天津市测绘院，天津 300381)

随着网络地图的兴起以及地理信息在各行业中的应用，兴趣点已经成为地理信息应用中不可或缺的一类要素，在地理信息应用中起到越来越重要的作用。但随之而来的，跨比例尺间的兴趣点取舍问题却成为地理信息应用中的一个难点。提出一种基于Delaunay三角网的跨比例尺点要素综合算法，结合空间和属性特征解决了跨比例尺兴趣点的取舍问题。

地图综合；Delaunay三角网；结点领域；空间聚类；生命周期

1 引 言

随着网络地图的广泛应用，兴趣点在地理信息应用中起到越来越重要的作用，而兴趣点的综合也成为地理信息应用中的一个难点。在跨比例尺时，考虑到点重要性程度的情况，兴趣点的取舍更加复杂。现有的点要素综合算法有基于遗传算法的点群目标选取模型，基于Voronoi图的点群目标普适综合算法等。基于遗传算法的点综合算法是先自适应分类，在每个子点群中利用凸壳化简方法进行选取[2]，此种算法具有分治的思想，有自适应能力，但算法中没有考虑到属性加权的情况；基于Voronoi图的点综合算法考虑拓扑信息，相应的改进算法也考虑了点重要性程度[3]，但此算法选取标准一成不变，对子点群不能区别对待，缺少自适应性，改进的算法中反复构造Voronoi图效率较低。本文在原有算法的基础上，提出一种基于Delaunay三角网的跨比例尺点要素综合算法，兼容已有算法的优点，摒弃已有算法的缺点。

2 相关概念

2.1 Delaunay三角网

1908年，俄国数学家M.G.Voronoi首先在数学上限定了每个离散点数据的有效作用范围，并定义了二维平面上的Voronoi图。1934年，俄国数学家B.Delaunay由Voronoi图演化出了更易于分析应用的Delaunay三角网[6]。

Delaunay三角网具有最大最小角特性和空外接圆特性，即任意三角形的外接圆不包含其他结点，这使它最大限度地避免了尖锐内角的出现。在地图综合种可利用该模型进行目标间邻近关系的搜索和冲突探测[1]，另外，Delaunay三角网外围边界构建的是一个凸壳，且三角网的对偶图形为Voronoi图，这两个性质也可在地图综合算法设计中进行利用，如图1所示。

图1 Delaunay三角网、Voronoi图

2.2 结点领域

Delaunay三角网的对偶图为Voronoi图，也即Voronoi图中的每个单元内有且只包含一个结点，那么，我们定义此单元为包含结点的领域，用单元的面积度量结点领域的大小，面积越大，结点领域越大。

如果结点在点集的凸壳边线上，那么，取凸壳和Voronoi图的相交部分的面积作为结点的领域，因为只考虑结点占据点集内部空间的面积，而不涉及点集的外部空间。

在空间中，结点领域越大，那么，结点的空间重要性就越大。

2.3 生命周期

在地图表达空间中，每一个空间实体存在的尺度范围都是有限的[4]，以独立地物中的报刊亭为例，在大比例尺如1∶500地形图中，以点的形式表达，在小比例尺如1∶25万地形图中则不表达。空间数据在尺度上的展示，犹如自然生命一样，有出生也有死亡，也即拥有生命周期。

我们借用自然生命的生命周期的概念，定义空间数据的生命周期L为:

其中S0为起始比例尺，Sn为终止比例尺。

那么，兴趣点在生命周期内作为选取目标考虑，在生命周期外则不予考虑。

2.4 空间聚类

空间聚类是将空间对象几何划分为由相似对象组成的多个簇的过程。同簇内的对象之间具有尽可能大的相似性，而不同簇的对象之间则具有较大的差异性，从而有助于人们认识现象的整体分布模式。在GIS研究中，学者们将计算几何、图论方法与传统的聚类分析方法结合衍生出了面向空间目标的空间聚类方法。本文将利用Delaunay三角网的特性进行空间聚类。

3 本算法的实现步骤

地理要素的制图综合涉及两方面的内容，一是空间位置的综合，实际表现为图形上的缩减；二是属性方面的综合，实际表现在语义方面的缩减，在地理信息数据模型中，属性以属性项的方式辅助图形上的缩减。本算法综合考虑这两方面的内容，基于Delaunay三角网的特性设计出能够应用于跨比例尺的点要素综合的算法，算法步骤如下。

3.1 设定兴趣点的生命周期，确定综合所需点集

确定综合目标点集是综合算法的第一步，本文先从属性方面入手，通过设定点的生命周期，从语义上剔除不需进行图形缩减的兴趣点。

首先，根据地物的重要性和项目的具体需求，设置兴趣点的生命周期，例如，独立地物点中，报刊亭的生命周期L1=[1/100，1/1万]，即报刊亭的存在于1∶100比例尺到1∶1万比例尺之间；三甲医院的生命周期L2=[1/100，1/25万]。

其次，根据综合前后的比例尺，对照各类兴趣点的生命周期，选取需要综合的兴趣点集。

3.2 建立Delaunay三角网

如图2所示，对3.1所得的兴趣点集，建立Delaunay三角网，本文采用了扫描线算法[7]生成Delaunay三角网。

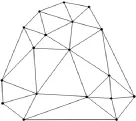
图2 Delaunay三角网

3.3 求得兴趣点的领域

根据结点领域的定义，通过Delaunay三角网求得对偶图形Voronoi图，得到Voronoi图的每个单元的面积，并将面积付给单元内的结点。

3.4 空间聚类

根据国家相关标准和综合项目要求，确定两兴趣点间的最短距离为minD，依据Delaunay的特性，先将三角形进行聚类后，再通过三角形的聚类子集求得兴趣点子集。

输入:三角形集D。

输出:兴趣点集P1，P2，P3，……，Pn

步1:取三角形集D中的一个三角形，此三角形三边长度都小于等于min D或只有一边长度大于min D，以此三角形作为三角形子集D1。

步2:取三角形集D中剩余的任意一个三角形X，X∈D。如图3所示，三角形X的三个顶点为A，B，C。计算三角形X的三边长度S1，S2，S3。

步3:循环所有三角形子集{D1，…，Dn}，针对每个三角形子集Dm，m∈{1，...，n}，判断Dm中是否存在三角形X的相接三角形。如果存在，转到步4。如果所有三角形子集中都不存在三角形X的相接三角形。那么，新增三角形子集Dn+1={X}。

步4:三角形子集Dm中存在三角形X的相接三角形。如图3所示，如果三角形X的三边长度都小于等于min D或只有一边长度大于min D，那么，将三角形X加入到三角形子集Dm中，否则，新增三角形子集Dn+1={X}。

图3 三角形X

步5:转到步2，直到三角形集D中所有符合条件的三角形都被取过为止。

步6:得到三角形子集D1，D2，…，Dn。如图4所示的画红杠的三角形被删除后，得到三个三角形子集。

图4 三角网聚类

步7:针对每个三角形子集，去掉重复的三角形顶点，得到兴趣点子集P1，P2，P3，…，Pn。

3.5 处理各个兴趣点子集

取兴趣点子集PX，X∈{1，...，n}，则综合的结果应为子集PX的一个子集Pend，并且Pend中任意两点之间的距离都大于min D。步骤如下:

输入:兴趣点集P1，P2，P3，…，Pn。

输出:综合结果兴趣点集P。

步1:取兴趣点子集PX，X∈{1，...，n}。

步2:取Px中的一点S，点S的领域在子集Px中的最大。以点S初始化Pend={S}。

步3:取Px的任意一点M，M∈Px且M∈Pend。如果点M到Pend中的任意一点的距离都大于min D，那么，将点S加入到Pend中。否则进行下一步。

步4:转到步3，直到PX中所有符合条件的点都被取到。

步5:得到子集Px的一个子集Pend，将Pend中的点加入到综合结果兴趣点集P中。

步6:转到步1，直到所有的兴趣点集都被取到。步7:得到综合结果兴趣点集P，如图5所示。

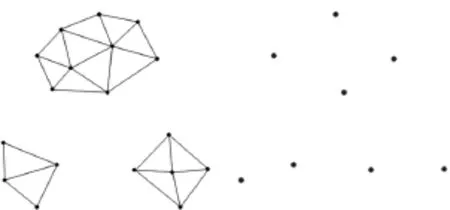
图5 综合结果

在步3中，计算M到Pend中的任意一点的距离，可以通过属性对距离进行加权。例如，医院和学校之间D，在加权后为1.2∗D再与min D进行比较，这样既考虑了空间方面的制约，又考虑了属性方面的影响，在此子集范围内能够做到一定程度的自适应。

4 结 论

本文根据兴趣点要素的特点，先从属性入手，应用生命周期概念，对兴趣点进行初步筛选，然后，通过建立Delaunay三角网，得到结点领域，进行空间聚类，将兴趣点按照空间邻近性分类一个个点集，之后，针对各个点集，以其中结点领域最大的点为起点，集合空间位置和属性两方面的信息，处理各个点集，得到最终结果。本文所提的算法，既考虑了兴趣点的全局分部特征，又针对局部进行区别对待；既考虑了点的空间位置的重要性，又考虑了属性信息的影响，并且，本算法中的步骤大部分都是应用Delaunay三角网的特性，相对反复构造Voronoi图来说，效率有所提高。

[1] 艾廷华，郭仁忠，陈晓东.Delaunay三角网支持下的多边形化简与合并[J].中国图象图形学报，2001，6(7):707～709.

[2] 邓红艳，武芳，钱海忠等.基于遗传算法的点群目标选取模型[J].中国图象图形学报，2003(8):133～135.

[3] 闫浩文，王家耀.基于Voronoi图的点群目标普适综合算法[J].中国图象图形学报，2005(5):665～668.

[4] Cecconi A.Integration of Cartographic Generalization and Multi-Scale Databases for Enhanced Web Mapping[D]. Zurich:University of Zurich，2003.

[5] 艾廷华，李静忠.尺度空间中GIS数据表达的生命期模型[J].武汉大学学报·信息科学版，2010 35(7):756～762.

[6] 普雷帕拉塔FP，沙莫斯MI.计算几何[M].北京:北京科学出版社，1992.

[7] V.Domiter，B.Zalik.Sweep-line algorithm for constrained Delaunay triangulation[J].International Journal of Geographical Information Science，2008，22(4):449～462.

[8] 孙家广，杨长贵.计算机图形学[M].北京:清华大学出版社，2000.

M ulti-scale M ap Generalization Algorithm of Point Feature Based on Delaunay Triangulation

Liu Huaqiao，Shu Bin，Zhou Yijun
(Tianjin Institute of Surveying and Mapping，Tianjin 300381，China)

With the rise of the network map，and geographic information applications in various industries，interest points has become an integral part of the geographic information features and play an increasingly important role in the geographic information application.But the ensuing cross-scale interest point trade-off has become a difficult geographic information applications.This paper presents a delaunay triangulation-based cross-scale point feature algorithm combining spatial and attribute characteristics to solve the problem of cross-scale interest point of the trade-offs.

map generalization；delaunay triangular；node domain；spatial clustering；life period

1672-8262(2013)04-42-03

P208.1，P209

B

2012—11—22

柳华桥(1980—)，男，工程师，注册测绘师，主要从事工程测量、地理信息系统等方面的工作。