电力系统无功优化方法综述

郭经韬，陈璟华，周 俊，许伟龙

(广东工业大学自动化学院，广州510006)

电力系统无功优化问题是一个多目标、多约束、多变量的混合非线性问题，涉及无功补偿装置投入地点的选择、无功补偿装置投入容量的确定、变压器分接头的调节和发电机机端电压的配合［1］。随着电力系统的日益发展，各种分布式发电方式电源的不断接入和智能电网的不断发展，对电力系统的潮流和稳定又产生了新的影响，无功优化问题也随之变得更加复杂，要求有更为有效的方法来适应时代的需要。

1 无功优化数学模型

无功优化的数学模型包括目标函数和约束条件两部分。综合电力系统无功优化的目标函数和约束条件，可以把具体的优化模型化为一般的数学模型:

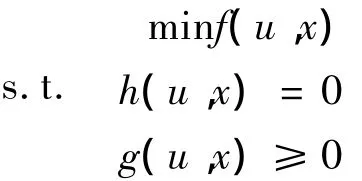
式中:u为控制变量(包括无功补偿装置投入的容量、变压器分接头的档位和发电机机端电压);x为状态变量(包括除平衡节点外其它所有节点的电压相角、除平衡节点和PV节点外节点的电压幅值、PV节点的无功出力);f(u，x)为无功优化目标函数;h(u，x)为等式约束条件(潮流约束);g(u，x)为不等式约束条件(变量约束)。

2 无功优化算法

2.1 传统的无功优化算法

2.1.1 非线性规划法

1968年，H．W．Dommel和 W．F．Tinney首次提出了简化梯度法，其特点是对罚函数和梯度步长的选取要求很严格，在接近最优点时会出现最速下降搜索方法的锯齿现象，收敛慢，不能有效处理函数不等式约束等问题。之后的牛顿优化算法［2］基于拉格朗日乘数法，利用目标函数二阶导数组成的海森矩阵与网络潮流方程一阶导数组成的雅可比矩阵来求解，充分利用海森矩阵与雅可比矩阵高度的稀疏性，一定程度上提高了收敛速度。文献［3］先将目标函数二次化、非线性约束线性化，成功地将二次规划法应用于电力系统无功优化问题的求解。这种方法的数学模型建立比较直观，物理概念清晰，计算精度较高。以上算法不同程度存在计算量、内存需求大，收敛性差，稳定性不好，对不等式的处理存在一定困难等问题，使其应用受到一定限制。

基于非线性规划法所存在的缺陷，不少研究人员不断对此算法进行改进。如文献［4］建立了一种含离散变量的电力系统无功优化的非线性互补约束模型，并提出相应的现代内点非线性互补算法，结果表明该算法收敛性较好、计算速度较高，对离散变量的大规模电力系统无功优化问题，能较好地满足运行需要。

2.1.2 线性规划法

线性规划法由 Maliszewski．R．M 于1968年首先并提出应用于电力系统无功优化的领域［5］，其原理是把目标函数和约束条件全部用泰勒公式展开，略去高次项，使非线性规划问题在初值点转化为线性规划问题，用逐次线性逼近的方法来进行解空间寻优。但对无功优化模型中的目标函数进行线性化时，会给最优解的取得带来一定的误差;在线性逼近的求解过程中，若步长取得过大，可能引发振荡，步长太小，又易使收敛变慢。灵敏度分析法［6］和直接法［7］是对线性规划法的发展，由于也存在局部收敛和难以处理离散变量的问题，虽有不少改进，但都不同程度上存在上述局限。

内点法是美国贝尔实验室的Karmarkar于1984年首先提出来的［8］，它从初始内点出发，沿着最速下降方向，从可行域内部直接走向最优解，因此被称为内点法。由于是在可行域内部寻优，故对大规模线性化问题，当约束条件和变量数目增加时，内点法的迭代次数变化较少，收敛性和计算速度均优于单纯形法。随着内点法的不断发展，逐渐形成三大类内点算法:投影尺度法、仿射尺度法和路径跟踪法，其中路径跟踪法正发展成为一般非线性规划的内点算法，是最具潜力的一类内点算法。文献［9］提出了一种基于预测—校正原对偶内点法的无功优化新模型，测试结果验证了所建模型与方法的正确性与有效性。

2.1.3 混合整数规划法

混合整数规划法的原理是首先确定整数变量，然后采用类似线性规划法的数学模型来处理离散变量，并用整数规划法的数学方法对其进行求解。此方法是通过分支—定界法不断定界以缩小可行域，逐次逼近全局最优解，能够有效地解决优化计算中变量的离散性问题。这类算法的弊端在于计算时间属于非多项式类型，随着维数的增加，计算时间会急剧增加，有时甚至是爆炸性的。文献［10］将混合规划法分解成整数规划和线性规划两个子问题，减少了求解问题的规模，在计算灵敏度矩阵时采用分块矩阵求逆法，节省了计算的时间。

2.1.4 动态规划法

动态规划法是研究多阶段决策过程最优解的一种有效方法，对目标函数和约束条件没有严格的限制，所得的最优解常常是全局最优解。该方法与其它方法结合，可减少计算量，提高计算速度，对解决无功优化控制问题具有较好的应用前景。但存在“维数灾”问题，使解题困难或无法进行;而且这种方法不存在标准的数学构成，要正确构成一个实际问题的动态数学规划模型比较困难。文献［11］提出了一种配电网无功补偿的动态优化算法，先将动态优化问题分解为一系列单节点电容器动态优化子问题，然后通过迭代求解一系列子问题的方式得到整个动态优化问题的最优解，结果表明算法是可行和有效的。文献［12］给出了一种动态无功优化空间－时间解耦的一种新方法，该方法数学模型较为清晰简单，便于实现，且时刻保证了以网损值最小为依据分配动作时间，结果表明能较好地满足动态次数约束下整体优化系统的无功，达到有效降低系统在一天内的有关损耗的目的。

2.2 人工智能算法

2.2.1 遗传算法(GA)

遗传算法是由美国密执安大学的Holland．J．H教授在1975年提出的，目前是模拟进化优化算法中最主要的，也是在电力系统中应用最多的一个分支。其核心思想是模拟自然界生物进化过程的随机搜索方法，采用多路径搜索，对变量进行编码处理，用对码串的遗传操作代替对变量的直接操作，从而可以较好地处理离散变量。它用目标函数本身建立寻优方向，且可以方便地引入各种约束条件，更有利于得到最优解，适合于处理混合非线性规划和多目标优化。虽然算法在解决多变量、多约束、多峰值、非线性、离散等问题有独有的优势，但存在局部收敛的问题，而且收敛速度难于满足实时控制的需要。

由于遣传算法本身存在的缺陷，许多学者提出了不同的方法对其进行改进。其中包括对编码方式、适应度函数、选择操作、交叉操作、变异操作和终止原则的改进，同时还结合了其它的算法，优势互补。如文献［13］是基于遗传算法和内点法的无功优化混合策略，仿真结果表明在计算速度和优化效果方面都具有明显优势。文献［14］给出小生境遗传算法在无功优化中的应用研究，此算法可用共享度改变个体的适应度，同时加速淘汰适应值低的个体，提高每一代个体的平均适应值水平以减少迭代次数，仿真结果表明该算法迭代次数明显少于基本遗传算法，提高了收敛速度。2.2.2 模拟退火算法(SA)

算法最早的思想是由Metropolis在1953年提出的，Kirkpatrick在1983年成功将其应用于组合优化问题中。算法的核心思想在于模拟热力学中液体的冻结与结晶或金属溶液的冷却与退火过程，把组合优化问题的目标函数看成退火系统的能量函数，如果以控制参数作为退火温度，SA寻找基态的过程就是令目标函数极小的过程。但其参数的选取比较复杂，为了使最终解尽可能接近全局最优，退火过程不能太快，这又使算法的计算时间过长。

文献［15］用模拟退火算法求解多状态的离散无功优化问题，并给出了仿真算例。文献［16］建立了一种二层规划数学模型，其中上层采用遗传算法求解，下层采用模拟退火法求解，最后仿真技术表明所建立的模型和算法有效可行，能一定程度上提高计算速度。文献［17］提出一种将遗传算法与模拟退火算法及牛顿下山法相结合的混合求解算法，以仿真算例对算法的性能和求解精度进行测试，结果表明该算法具有较好的计算速度和收敛性。

2.2.3 禁忌搜索算法(Tabu Search，TS)

算法是1986年由Glover首先提出来的，它采用禁忌技术，能在搜索过程中获得知识，并用以避免局部极值点，是一种收敛性较好的智能算法，但它不能在整个寻优空间同时开始搜索，因此初值的好坏直接影响到算法的收敛速度和解的质量。文献［18］提出了遗传禁忌混合算法:针对无功优化过程中控制变量的离散性和连续性相混合的特点，提出了混合编码策略并相应地采用启发式算法进行杂交，保持了遗传算法和禁忌搜索算法的优点，结果表明具有较好的收敛性和较强的全局寻优能力。文献［19］提出将主动禁忌搜索(RTS)算法用于配电网无功电压优化控制问题的求解，并与传统的禁忌搜索比较，证明有更好的灵活性和更高的求解效率。文献［20］在传统遗传算法的基础上，结合模拟退火算法概率性的突跳搜索机制和禁忌搜索算法能避免迂回的领域搜索机制提出一种混合算法，并证明其可提高计算速度、收敛性能和计算效率。

2.2.4 粒子群算法(PSO)

粒子群算法是由Kennedy和Eberhart于1995年提出的一种模拟鸟群觅食过程中迁徙和群集行为的智能算法［21］。粒子群算法需要用户确定参数较少，而且操作简单，但在计算后期收敛较慢，容易陷入局部最优点。对粒子群算法的改进归结起来基本都是在以下方面进行的:参数设置、粒子多样性、种群结构和算法融合。文献［22］提出了一种新颖的用于求解无功优化问题的分布式协同粒子群优化算法，考虑到大规模电力系统集中优化难度较大，采用分层控制中的分解－协调思想将大系统分解成若干个独立的子系统，有效地降低求解问题的复杂度，并采用混合策略在各个子系统间进行协同优化，结果证明提出的方法能够获得高质量的解，并且计算时间短、效率高。文献［23］提出一种基于适应度空间距离评估选取最优解的多目标粒子群算法，该算法避免了多目标优化求解方法中权重选择的难题，保证了寻优方向的多向性，可以获得多目标优化问题的Pareto解集，算例表明在有效性和最优性等方面均有良好表现。文献［24］提出一种基于向量评价的自适应粒子群算法(VEAPSO)来解决多目标无功优化问题，求解出问题的Pareto解集。为从解集中选取合适的最优解，提出一种基于决策者偏好及投影寻踪模型的多属性决策法，使决策结果更加真实可靠，算例表明了该方法的有效性。

2.2.5 模糊优化算法

模糊优化算法源于模糊理论，利用模糊集将多目标函数和负荷电压模糊化，给出各目标函数隶属函数，将问题转化为标准的线性规划和非线性规划处理。由于其所需的信息量少，智能性强，迭代次数少，所以计算速度快于非模糊控制并能较好地反映电压的变化情况，容易在线实现。模糊算法只对一些不确定性问题分析有效，对于精确的概念会使问题复杂化。文献［25］提出了一种结合multi－agent系统和粒子群优化技术，算例结果表明该算法具有较高质量的解，收敛性好、运行速度快。文献［26］运用模糊聚类分析法将系统分区，并基于电压幅值对无功功率的灵敏度定义了电力系统各节点间的电气距离，对待分类对象的全体作适当的标定，运用传递闭包法求出动态分类，通过计算统计量F最后得出最优分类，结果表明该方法所占内存小、计算速度快。

2.2.6 混沌优化算法

将混沌优化方法用于一类连续复杂对象的优化问题，结果表明混沌优化算法比SA等随机优化算法的效率更高。但它也有缺点，即当搜索起始点选择不合适或遍历区间很大或控制参数选取不合适时，搜索结果很难达到或接近最优解，或算法可能需要花费很长的时间才能取得较好的优化性能。文献［27］提出一种混沌粒子群优化方法，以克服粒子群优化中容易出现早熟的问题，该方法结合混沌变量良好的遍历性及混沌优化的特点，对即将重合而引起搜索能力下降的粒子赋予混沌状态搜索，从而提高搜索效率。文献［28］提出一种变尺度混沌优化算法，利用混沌运动的内在随机性、遍历性和规律性进行全局寻优;通过尺度变换不断缩小优化变量的搜索空间，通过“二次搜索”的调节系数提高搜索精度，从而提高局部细化搜索能力，最后由算例验证其有效性。文献［29］针对多目标函数解的不足，提出了混沌免疫混合算法的多目标无功优化，算例结果证明其正确性和可行性。2.2.7 其它算法

专家系统、人工神经网络、鱼群算法、蚁群算法、搜寻者算法、多Agent技术等都被不断引入到无功优化领域中，由于各种算法本身都或多或少存在缺陷，就促使这些算法不断地与其它算法结合，优势互补，使算法的研究更上了一个台阶。

3 结论

随着电力系统的不断发展，配电网络由于分布式电源的接入使电网结构更加复杂，使电网潮流的研究迈入一个新的阶层。电力系统无功优化作为最优潮流的重要一支，对其优化性能和算法的研究也会百花齐放。但就目前而言，无功优化问题至今仍未有一个完整有效的方法，所以对新算法的研究和多种算法的混合算法还需进行深入研究。

［1］ 陈海焱，陈金富，段献忠．含风电机组的配电网无功优化［J］．中国电机工程学报，2008，28(7):40 －45．

［2］ 严正，陈雪青，相年德，等．优化潮流牛顿算法的研究及应用［J］．清华大学学报，1989，29(1):69 －78．

［3］ 沈如刚．电力系统无功功率综合优化——二次规划法［J］．中国电机工程学报，1986，6(5):40 －48．

［4］ 李滨，韦化，李佩杰．电力系统无功优化的内点非线性互补约束算法［J］．电力自动化设备，2010，，30(2):53 －58．

［5］ QIU J，SHAHIDEHPOUR S M．A new approach for minimizing power losses and improving voltage profile［J］．IEEE Trans on Power system，1987，2(5):287 －295

［6］ MARIA G A，FINDLAY J A．A new optimal power flow for ontario hydro EMS［J］．IEEE Trans on Power Systems，1987，2(10):576－584．

［7］ IBA K，SUZUKI H，SUZUKI K － I，et al．Practical reactive power allocation operation planning using successive linear programming［J］．IEEE Trans on PS，1988，3(2):558 －566．

［8］ KARMARKAR N．A new polynomial－ time algorithm for linear programming［J］．Combinatorial，1984，4(4):373 － 395．

［9］ 余娟．基于预测—校正原对偶内点法的无功优化新模型［J］．中国电机工程学报，2005，25(11):146 －151．

［10］ RAMA l S，RAMACHANDRAN K，HARIHARAN S．Optimal reactive power allocation for improved system performance［J］．IEEE Transactions on Power Apparatus and System，1984，103(6)．

［11］刘蔚，韩祯祥．配电网无功补偿的动态优化算法［J］．中国电机工程学报，2006，26(10):79 －85．

［12］杨悦，李国庆．配电网动态无功优化空间－时间解耦的一种新方法［J］．电力系统保护与控制，2010，38(21):39 －43．

［13］刘方，颜伟，DAVID C．Yu．基于遗传算法和内点法的无功优化混合策略［J］．中国电机工程学报，2005，25(15):67 －72．

［14］向铁元，周青山，李富鹏，等．小生境遗传算法在无功优化中的应用［J］．中国电机工程学报，2005，25(17):48 －51．

［15］ Ying－Tung Hsiao，Chun－Chang Liu．A new approach for optimal VAR sources planning in large scale electric power systems［J］．IEEE Transactions on Power Systems，1993，8(3):988 －994．

［16］王淑芬，万仲平，樊恒，等．基于二层规划的无功优化模型及其混合算法［J］．电网技术，2005，29(9):22 －25．

［17］刘科研，盛万兴，李运华．基于改进遗传模拟退火算法的无功优化［J］．电网技术，2007，31(3):13 －18．

［18］谭涛亮，张尧．基于遗传禁忌混合算法的电力系统无功优化［J］．电网技术，2003，28(11):57 －61．

［19］杨银国，张伏生，贺春光，等．配电网无功电压优化控制求解的一种新方法［J］．电力系统自动化，2005，29(9):45 －49．

［20］王春娟，张伏生，王帅，等．基于混合优化算法的电网规划方法［J］．电网技术，2005，29(23):30 －39．

［21］ KENNDY J，EBERHART R C．Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neutral Networks．Perth，Australia，1995:1942 －1948．

［22］赵波，郭创新，张鹏翔，等．基于分布式协同粒子群优化算法的电力系统无功优化［J］．中国电机工程学报，2005，25(21):1－7．

［23］娄素华，吴耀武，熊信银．基于适应度空间距离评估选取的多目标粒子群算法在电网无功优化中的应用［J］．电网技术，2007，31(19):41 －46．

［24］刘佳，李丹，高立群，等．多目标无功优化的向量评价自适应粒子群算法［J］．中国电机工程学报，2008，28(31):22 －28．

［25］赵波，曹一家．电力系统无功优化的多智能体粒子群优化算法［J］．中国电机工程学报，2005，25(5):1 －7．

［26］杨秀媛，董征，唐宝，等．基于模糊聚类分析的无功电压控制分区［J］．中国电机工程学报，2006，26(22):6 －10．

［27］刘自发，葛少云，余贻鑫．基于混沌粒子群优化方法的电力系统无功最优潮流［J］．电力系统自动化，2005，29(7):53 －57．

［28］娄素华，吴耀武，熊信艮．电力系统无功优化的变尺度混沌优化算法［J］．电网技术，2005，29(11):20 －29．

［29］熊虎岗，程浩忠，胡泽春，等．基于混沌免疫混合算法的多目标无功优化［J］．电网技术，2007，31(11):33 －37．