生物医学信号模式的状态评估法分析方法研究*
杨 禹,严中红,易 东
(1.第三军医大学卫生统计学教研室,重庆400038;2.重庆理工大学药学与生物工程学院 400050)
医疗信息系统中存在许多近似连续的周期信号,例如心电、脉搏、心音、呼吸信号等。对这些信号的采集和分析主要有三大基本任务:(1)信号在时域或频域基础上的定位和分割;(2)建立在信号分析和学习基础上的信号分类和识别;(3)基于医疗和临床诊断的统计分析和评估。在频域上,经常需要确定频率和频率变异、频率分布;在时域上,将时域周期化,统计每个周期信号所具有的共同特征,由此找出某些特征信号以及分类特征信息。
在心电图中QRS波具有的复杂性,对心律不齐、异常心音的诊断非常重要[1]。对其分析的主要任务是:对QRS波进行信号分割;分割完成后进行模式描述;在此基础上完成模式评估。本文提出了一种全新的状态表示方法(state representation methodology,SRM)[2],运用文献[3]中的方法实现对心音信号的分割,然后对心音信号的特征分析可以通过频率切片小波变换(frequency slice wavelet transform ,FSWT)来实现,提取信号的时频特征,通过SRM建模方法,进一步建立心音的评估模型,并用QRS波数据进行验证性研究。
1 资料与方法
1.1 一般资料 本文数据采集由日本山本文数口大学与重庆理工大学[2]、第三军医大学[1]合作完成,采用3MTMLittmann®3200型电子听诊器与迈瑞BeneHeart R3心电图机收集数据。研究纳入总人数120例,健康自愿者40例,异常病例80例。
1.2 方法
为了使用新的SRM评估方法[2],临床数据采集只把分为正常与异常两部分。临床正常心音信号,由部分学生与医院志愿者配合完成,心电信号作为辅助验证信号。临床异常心音信号包括了多种症状的心脏疾病临床病例,病例由电脑随机抽选进行测试。
1.2.1 SRM 模型的 建立 SRM 采 用与 RSM[4]或 SVM[5-15]相似的观点来描述系统状态。其不同之处在于SRM中响应是已知的而预测器(即系统的状态)一般是未知的。因此,使用SRM方法将建立一个新的系统状态预测模型,该模型将具有与SVM相类似或相同的方程[5-8]。但用一个简单的尺度概念来取代 VC维(vapnik-chervonenkis dimension)[5-15]。
SRM试图为系统模式识别提供一个新的思路,同时SRM作为一个更广泛的理论可以实现对系统状态的非参数描述。应用SRM方法可证实如下结论:(1)SRM首先接受这些事实:观测数据的不确定性和不完备性;(2)SRM假定系统状态是系统响应环境刺激的函数,它是系统的结构参数和响应特性对偶关系的量化;(3)当系统能满足正常的使用属性,则认为该系统是处于正常的状态,此时SRM定义系统状态变量为一个常数,否则系统状态变量就不会是一个常数;(4)SRM认为任何一个系统的两个状态都存在有差异,但差异的大小取决于所观察的尺度,大尺度下呈现出较小的差异,小尺度下呈现出较大的差异。
SRM 模型可表示为:

ζ是系统的状态变量;λ和x是关于系统的结构参数和响应特性;参照SVM中的核函数的方法,引入观察尺度σ,则SRM状态函数可以改写为:
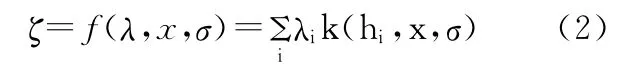
hi和x是相对于系统的响应特征;式(2)可以进一步由SRM工具来处理;对系统的响应特征x可采用频率切片小波变换方法(FSWT)来分析和提取[2,16-18]。
1.2.2 基于SRM模型的识别方法与步骤 针对类似于正常心音信号和心电信号的时间序列生物医学信息模式(biomedical signal pattern,BSP),在建立SRM模型后,进一步就是解决基于SRM模型的模式识别问题了,通常需要解决下面几方面的问题:(1)如何从临床信息中通过SRM方法描述患者的状态?(2)如何通过SRM方法来比较评估患者在两个临床阶段的状态?(3)如何按照某种特定的临床意义,通过SRM方法从一组相似患者的临床信息中描述他们的共同特征?(4)如何按照某种特定的临床意义,如何通过SRM方法对不同组病人之间的差异进行分类。
对于问题1,以心音为例,如果已经采集了临床患者的心音信号,通过文献[3]给出的方法将其分为m个周期,并将这些分段信号记为:S1,S2,……Sm作为对照,我们通过频率切片小波变换以瞬态阻尼参数的方法来分析系统特征,该方法在文献[2]中的第6和7节中给出。这样基于SRM模型,解决问题(1)的方法包含以下5个主要步骤:①计算信号特征;②解SRM特征模型;③通过SRM构建状态参量;④统计状态参量;⑤评估两个时期状态的变化。
问题2可以通过上面第⑤步来实现,关键的问题在于哪些包含于生物医学信号模式中的特征是重要的且能够反映生物学特性?因此,在正式应用之前,通常需要用实验仪器来验证诊断方法的有效性。
本研究也可以应用SRM定义的各种指标来评估问题1~4,对于一组患者的数据而言所采用的SRM方法是相似的。在讨论和解决了问题1和问题2后,每个患者的特征可以合并到一个模型中用以解决问题3,SRM方法也可以描述他们普遍的特征。作为SRM分析中关键的一步,问题3的复杂度决定于信号的全部特征。而频率切片小波变换为时频分析提供了一个全新的工具,它具有很高效率特别是对于动态响应和瞬时振动信号,频率切片小波变换可以方便地表示动态响应的特征[16-18]。
1.2.3 频率切片小波变换分析方法 对心音信号的特征分析可以通过频率切片小波变换(frequency slice wavelet transform,FSWT)来实现,提取信号的时频特征。注意到傅里叶变换和其反变换表示为
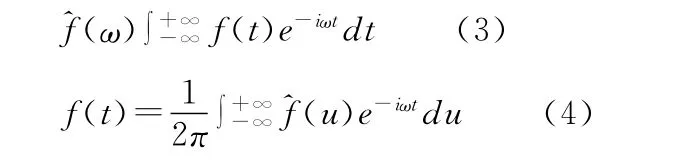
通过对短时傅里叶变换(STFT)的扩展,频率切片小波变换直接在频域定义为

其中k为特定的尺度参数。原始信号可以通过频率切片函数(frequency slice function:FSF)被分解,例如p(ω),它类似于小波基但是可以非常自由地设计。同时,原始信号f(t)又能通过频率切片小波变换的表示方法重建,而不受小波理论的严格限制。并且发展了若干新的时频特征。由于具有这些特性,频率切片小波变换在处理时变信号的时候更加灵活,在使用中易于分析和控制。频率切片小波变换不仅可以单独在频域表示每个模型,也能在时域正确地表现信号的细节。因此,频率切片小波变换的许多优点都适用于生物力学信号的动态特征。由此,频率切片小波变换可以用于发现生物医学信号模式的新特征,并动态地分析这些特征[16-18]。更多关于频率切片小波变换的信息请参见文献[2]。
1.3 统计学处理 利用Matlab平台,首先建立SRM模型,然后采用Matlab平台中提供的正态分布统计方法,分析系统状态随机变量的分布情况,其均值、方差为本文主要研究的统计参数,分析正常临床心音与异常心音信号的状态分布差异性。
2 结 果
下面以心音分析为例给出研究结果。按照前面解决问题1的实现方法,首先应用FSWT抽取心音(包括正常与异常两部分)的动态阻尼特征。然后先用40个正常心音建立SRM状态模型,得到如图1的正常心音状态分布模型。再用80个病例特征代入正常心音的SRM模式,得到异常心音状态的分布模型,见图2。其中σ=1是SRM模型的观察尺度。观察尺度越大正常与异常分布差异越小,尺度越小差异越大。从图1与图2得知,正常与异常两个病例集的状态值分布有明显的差异,有很好的区分度。
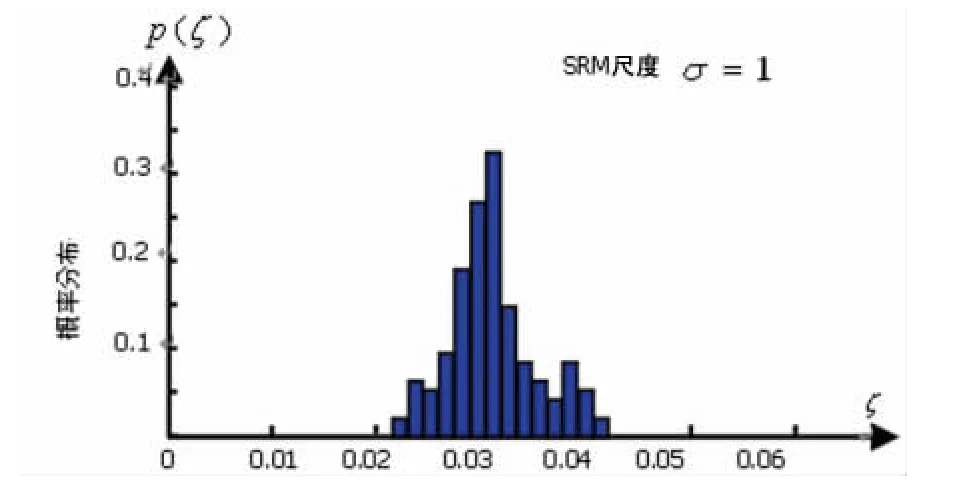
图1 正常心音的状态概率分布
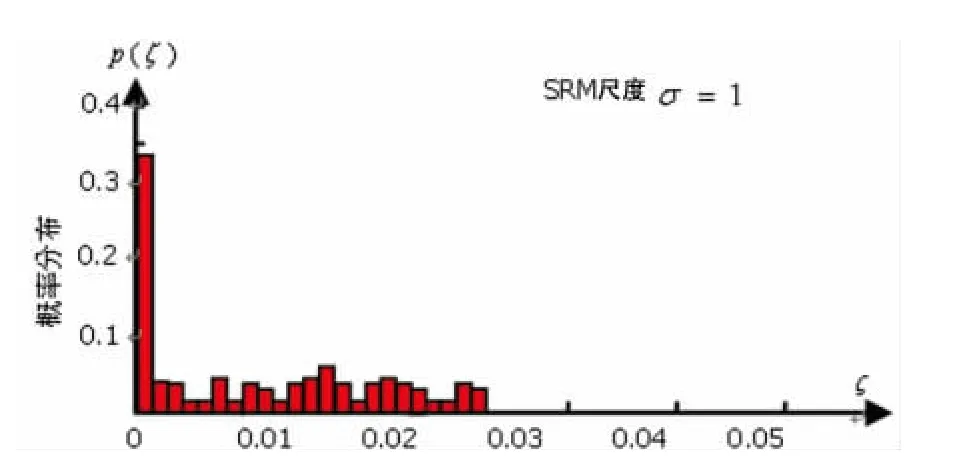
图2 异常心音的状态概率分布
3 讨 论
目前随着移动通讯技术的发展,越来越方便的便携式医疗设备受到人们的普遍欢迎,人们把心音和心电等信号作为重要的应用之一,试图开发基于自动分析技术的家庭心音心电早期预警系统,这就出现了需要实时评估,描述患者的病理状态特征等信号分析的任务。
传统的方法中,利用神经网络、支持向量机等模式识别方法去分析医学信号的模式,这些方法有它的积极作用,但是因为其计算复杂,同时它的特征能力提取有限,其适应性、实用性不够、特别是实时性很差。同时要建立一个计算过程收敛的学习模型难度大、耗时、往往需要复杂的技巧。
本文旨在介绍一种新的医学信号评估方法,从系统状态描述的角度出发,借用文献[2]提出SRM观点,首先接受了SRM关于系统状态的定义:SRM假定系统状态是系统响应环境刺激的函数,它是对系统的结构参数和响应特性对偶关系的量化。其本质上是一种非参数的系统描述方法,系统的状态计算是建立在系统特征的转换基础上的,SRM包括如何定义或记录系统状态变量,以及如何将这个变量描述成一个状态表示方程(SRE)。进而利用SRE计算系统状态变量。SRE可以被近似地认为是系统特征线性或非线性的结合。SRE可以进一步通过核函数法(KFM)[5]来描述,这对于SVM方法来说是经常使用的,而KFM通常是把SVM映射成一个高次非直线型方程。SRE解决状态变量的方法最终将转换成为一个大规模线性问题。对SRM的评估是基于概率的方法,且已经设计了几种算法[2]。文献[2]中采用的一些仿真例子表明SRM新方法相对传统方法而言更容易理解且应用简单。
本文把SRM用于BSP分析中。实验表明SRM它可以用于心音,心电和呼吸等信号分析。心音分析的第一步是周期分割,然后采用频率切片小波变换抽取每一个周期响应的动态特征。本文将收集的标本数据集仅分为两种类型:正常与异常两部分。先用健康自愿者数据建立SRM模型,这一步称为系统状态模型学习。接下来,用异常病例的数据代入该模型进行比较,判断两个分型的差异性,这一步称为系统模型检验。实验表明,患者的状态分布模型,反映了生物结构和生物力学响应的内在关系,两种分型的状态分布差异明显,SRM方法应用简单有效。
综上所述,由文献[2]提出的最早应用于桥梁安全评估的这些新思路和方法将成为一个强有力的开发工具,并能运用于生物力学的信号处理领域。目前,关于SRM,频率切片小波变换[16-17]工具和特征提取算法等方面还需要更多的研究工作,以便对此方法进行深入的讨论与改进。
[1]Jiang ZW,Choi S.A cardiac sound characteristic waveform method for in-home heart disorder monitoring with electric stethoscope[J].Expert Syst Appl,2006,31(2):286-298.
[2]Miyamoto A,Yabe A.State representation methodology and application to bridge condition assessments[J].J Civil Eng Archit,2012,6(4):433-443.
[3]Yan Z,Jiang Z,Miyamoto A,et al.The Moment Segmentation analysis of heart sound pattern[J].Comput Methods Programs Biomed,2010,98(2):140-150.
[4]AndréI,Siuli M.Response surface methodology[J].Wiley Interdiscip Rev Comput Stat,2010(2):128-149.
[5]Yilmaz I.Comparison of landslide susceptibility mapping methodologies for Koyulhisar,Turkey:conditional probability,logistic regression,artificial neural networks,and support vector machine[J].Environ Ear Sci,2010,61(4):821-836.
[6]丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.
[7]顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报:自然科学版,2010,50(7):1063-1066.
[8]顾亚祥,丁世飞.支持向量机研究进展[J].计算机科学,2011,38(2):14-17.
[9]巩知乐,张德贤,胡明明.一种改进的支持向量机的文本分类算法[J].计算机仿真,2009,26(7):165-168.
[10]舒双宝,罗家融,徐从东,等.一种基于支持向量机的人脸识别新方法[J].计算机仿真,2011,28(2):280-283.
[12]汪廷华,田盛丰,黄厚宽.特征加权支持向量机[J].电子与信息学报,2009,31(3):514-518.
[13]杜喆,刘三阳,齐小刚.一种新隶属度函数的模糊支持向量机[J].系统仿真学报,2009(7):1901-1903.
[14]叶圣永,王晓茹,刘志刚,等.基于支持向量机的暂态稳定评估双阶段特征选择[J].中国电机工程学报,2010(31):28-34.
[15]王克奇,杨少春,戴天虹,等.采用遗传算法优化最小二乘支持向量机参数的方法[J].计算机应用与软件,2009,26(7):109-111.
[16]Yan ZH,Miyamoto A,Jiang ZG.Frequency slice wavelet transform for transient vibration response analysis[J].Mech Syst Signal Process,2009,23(5):1474-1489.
[17]Yan ZH,Ayaho M,Jiang ZW.Frequency slice algorithm for modal signal separation and damping identification[J].Comput Struct,2011,89(1/2):14-26.

