底水气藏高速非达西渗流临界产量的一种确定方式

邱先强 （中国地质大学 （北京）能源学院，北京 100083）

邱伟 （中石化中原石油工程有限公司井下特种作业公司，河南 濮阳 457001）

宫红茹，陈艳春 （中石化中原油田分公司采油五厂，河南 濮阳 457001）

底水气藏是指在气藏储层中位于含气边界之内有地层水。气井最 “怕水”，见水气井会导致气相渗透率急剧下降，产量大幅降低。人们普遍认为，如果气井的配产超过了井的临界产量，那么该井必定见水，并且很快见水。因此，在设计合理产量时总以临界产量作为一个约束条件，控制其小于临界产量，以实现无水开采。与一般液体渗流规律不同，由于真实气体黏度低，流动性好，其流动规律一般符合高速非达西渗流规律。针对这一点，笔者从Dupuit临界产量计算公式的推导出发，推导出了在考虑真实气体高速非达西渗流下的临界产量方程并给出了其求解方法。

1 达西渗流下Dupuit临界产量计算公式

Dupuit在解决地下水工程问题时，首先提出 “临界产量”这一概念［1］。将该临界产量的计算公式应用于底水驱气藏之中，得到气井临界产量计算公式为［2］：

式中：qsc为标准状况下的气井产量，m3/d；Kg为气层的渗透率，D；Δρwg为水气密度差，kg/m3；h为气层有效厚度，m；b为气井射开厚度，m；Bg为气体体积因数，1；μg为气层气体黏度，mPa·s；re为气井排泄半径，m；rw为气井井筒半径，m；g为重力加速度，m/s2，一般取g＝9.807m/s2。

式 （1）的适用条件为：稳定渗流；均质地层；忽略因毛管力而引起的气水过渡带；气水密度及黏度为常数；渗流服从达西渗流规律。

2 考虑高速气体非达西渗流下临界产量计算公式

真实气体的高速非达西渗流用Forchheime方程描述为［3～5］：

式中：p为压力，Pa；μ为流体黏度，Pa·s；v为渗流速度，m/s；ρ为流体密度，kg/m3；r为径向渗流半径，m；K为渗透率，D；β为描述孔隙介质紊流影响的系数，称为速度系数，m－1。

其中常用的速度系数β计算公式为：

式中，渗透率K的单位为mD。

2.1 基本假设条件［6］

①忽略毛细管力而引起的气水过渡带；②气层均质，气水密度及黏度为常数；③气体渗流为等温渗流；④真实气体，存在高速渗流，服从非达西稳定渗流规律。

2.2 计算模型建立

在前面的假设条件下，参照李传亮［7］采用一种简单的推导过程。在径向r处取一微元体，相应与某产量qsc下形成的水锥高度在r处为z，如图1所示。其径向上的渗流速度表示为：

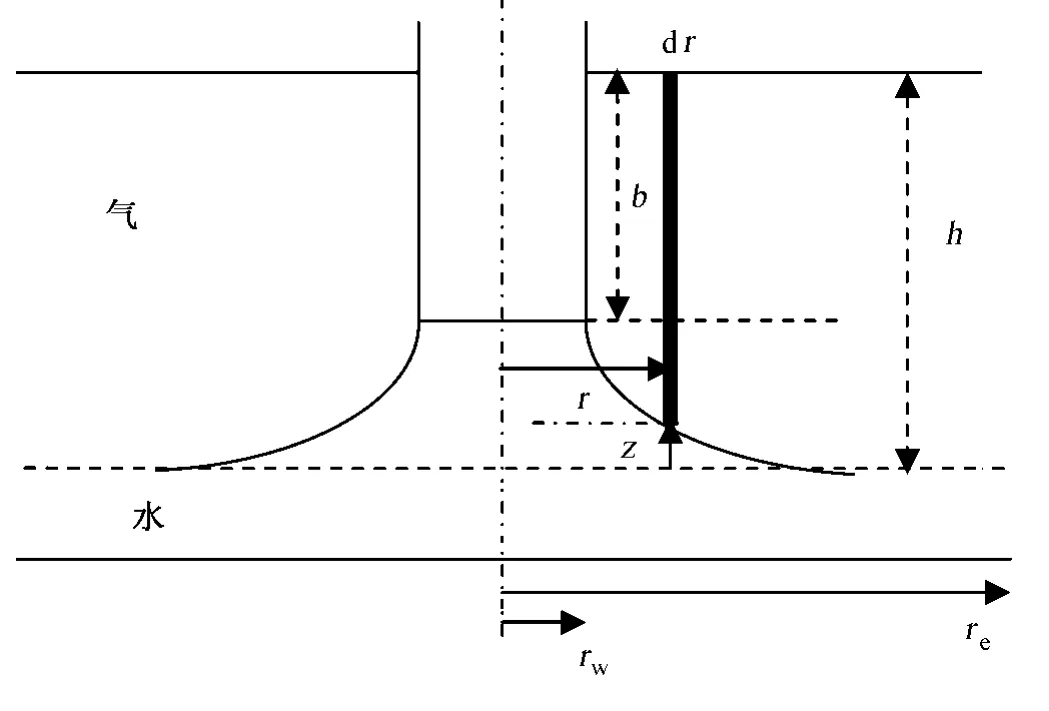
图1 气井临界产量流动微元示意图

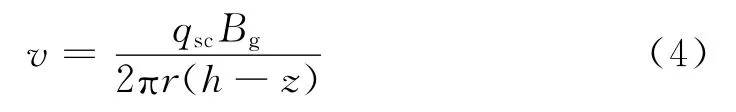
把式（4）代入式（2）中得到：

认为在r处的压力增量与气 －水界面上升增量存在如下关系（即向上的压差dp与气 －水界面上升dz的重力平衡）：

把式（6）代入式（5）中得到：

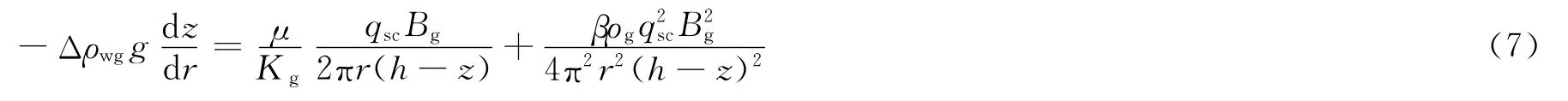
式中：ρg为气体密度，kg/m3。

由式（7）可整理得（并转化为SI实用单位制）：

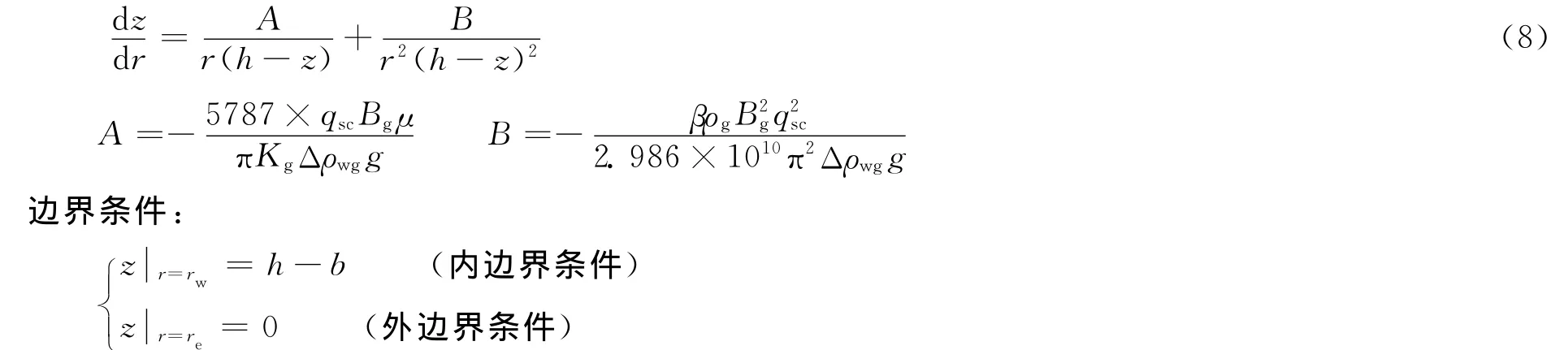
2.3 计算模型求解

建立的上述微分方程为非齐次，很难通过分离变量得到解析解，因此一般采用数值解法。笔者采用四阶龙格－库塔法［8］，并采用试算法求临界产量qsc，具体采用如下步骤进行迭代：① 试算时，任意设定一个qsc值（如qsc＝0.5×104m3/d），代入式（8）中；② 用四阶龙格 －库塔法求式（8）及内边界条件z（rw）＝h－b，划定步长，向前迭代直到算出z（re）的值；③如果算出的z（re）值满足外边界条件，即z（re）≈0，则该qsc值即为所求；④如果算出的z（re）≠0，可根据经验另选一个较大或较小的qsc值再代到式（8）中进行试算，直到有一个qsc满足z（re）≈0即可。

3 气井产量小于临界产量时的水锥形状

3.1 达西渗流下的水锥形状

从Dupuit产量模型中可得到水锥高度z为［2］：

式中：qg为气井产量，m3/d。式（9）表明了水锥高度z随径向r的变化规律。

3.2 高速非达西渗流下的水锥形状

在给定产量qsc下，通过式（8）及其边界条件求出的数值解，便可得到函数z＝f（r）在［rw，re］上的近似解，即水锥高度z随地层径向距离r变化的分布。

4 实例计算分析

某气层厚度20m，气体平均黏度0.0161mPa·s，体积因数0.00663，气层的渗透率0.0075D，孔隙度为0.15，排泄半径为400m，井半径为0.1m，射孔段长度5m，地层条件下气体的平均密度为65.23kg/m3，气水密度差为920kg/m3。

4.1 临界产量计算结果

应用式 （1）计算Dupuit临界产量为：

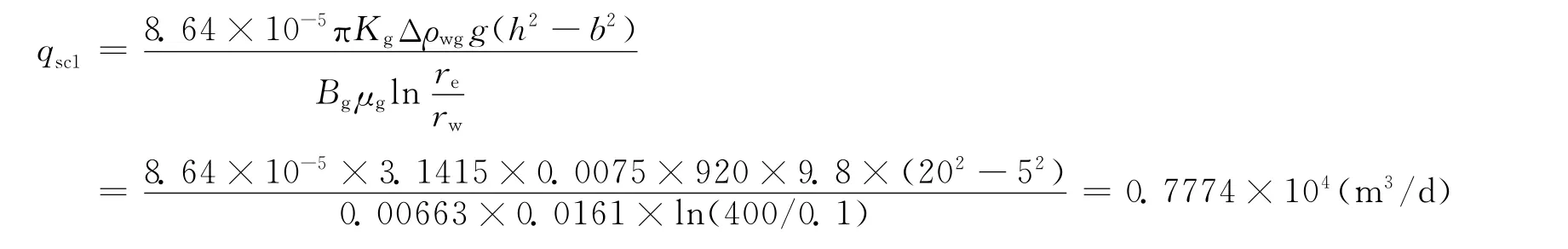
应用式（8）及其边界条件，把求解该计算模型的方法写于计算机Visual Basic程序。为了使数值解趋于精确，划步长Δr为0.05m。划的网格数为（re－rw）/Δr＝8000。试算得到高速非达西渗流下的临界产量qsc2＝0.72×104m3/d。

可以看到，在真实气体高速非达西流下的临界产量要小于达西渗流下Dupuit临界产量。这是因为在高速气流下，流体的惯性阻力不可忽略，气流的阻力增大，特别是在井底附近的压力梯度很大，底水更容易突破。

4.2 水锥形状高度模拟结果

图2是在产量qsc2＝0.72×104m3/d下计算得到的水锥高度的分布。从图2可以看出，由于在气井井底附近压力梯度很大，在这区域内水锥高度急剧上升，在r＝rw处，z值达到最大；在同样的产量下，非达西渗流下的水锥高度比达西渗流下的要略高，前者的水锥形状在后者的上方，底水突破得更为严重。

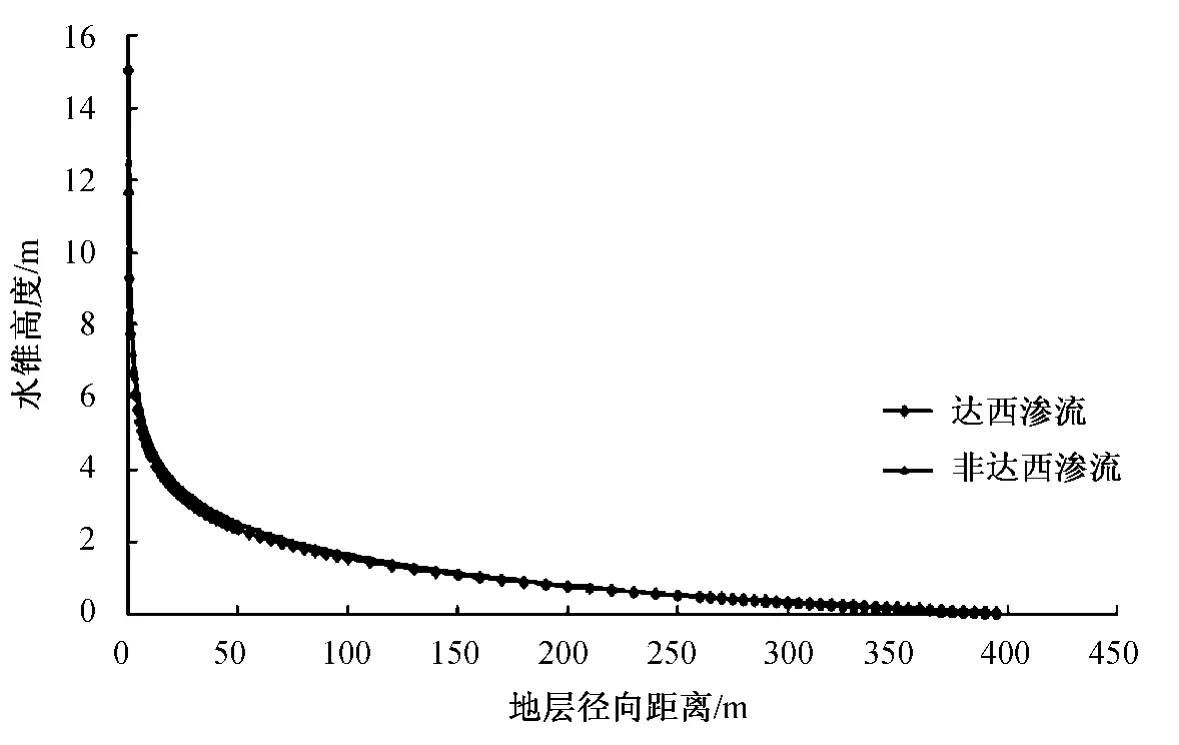
图2 底水气藏水锥形状

5 结 论

1）应用前面的临界产量的推导方程，两种模型下计算出的产气量都偏小，这仍需要进行深入的研究，并在实际的工作中要注意到这一点。

2）在真实气体高速流动下，流体的惯性阻力不可忽略，要考虑非达西效应。

3）在高速非达西稳定渗流的Forchheime方程基础上，建立底水气藏高速非达西渗流下的临界产量是一种新的尝试，并通过算例计算证明了其合理性。

［1］李传亮 .修正Dupuit临界产量公式 ［J］.石油勘探与开发，1993，20（4）：56～59.

［2］黄炳光，刘蜀知，唐海，等 .气藏工程与动态分析方法 ［M］.北京：石油工业出版社，2004.

［3］李晓平 .地下油气渗透力学 ［M］.北京：石油工业出版社，2007.

［4］Huang H，Ayoub J.Applicability of the Forchheimer equation for Non－Darcy flow in porous media［J］.SPE102715，2006.

［5］赵晓燕，姚军，崔传智 .考虑真实气体PVT动态的高速非达西渗流模型 ［J］.石油钻探技术，2009，37（2）：78～80.

［6］张烈辉，朱水桥，王坤 .高速气体非达西渗流数学模型 ［J］.新疆石油地质，2004，25（2）：165～168.

［7］李传亮 .油藏工程原理 ［M］.北京：石油工业出版社，2005.

［8］李庆扬，王能超，易大义 .数值分析 ［M］.北京：清华大学出版社，2008 .

［编辑］ 萧 雨