圆心设站测设曲线的实用方法研究
罗清松,罗尧东
(西南科技大学环境与资源学院,四川绵阳 621010)
圆心设站测设曲线的实用方法研究
罗清松∗,罗尧东
(西南科技大学环境与资源学院,四川绵阳 621010)
道路工程弯曲的地方一般需要加设缓和曲线和圆曲线作为直线道路的链接,对该类道路曲线工程,常用自由设站极坐标法对其进行详细测设。而基于自由设站极坐标法测设带有缓和曲线的曲线基础上,考虑带有缓和曲线的曲线测设中圆曲线圆心的特殊性,建立了将仪器架设在圆曲线圆心点上,采用偏角法一次性完成带有缓和曲线的曲线中线测设的可行性数学模型,并分析其原理和测设方法。结合算例验证了该方法的可行性和实用性且证实了该方法计算简单,测设过程简便、快速、实用,适用于施工现场。
曲线测设;圆心设站;缓和曲线;圆曲线;数学模型
1 引 言
线状工程包括铁路、公路、地铁隧道和轻轨等因线路过长总会受到地形、地物、地质及其他因素的约束,经常要改变路线前进的方向。当路线方向改变时,在转向处需要用曲线将两直线连接起来。除了直线,曲线已经成为线状工程必不可少的部分。而在一般情况下,直线与曲线之间需要增设缓和曲线作为链接,我国道路建设弯曲的地方采用螺旋线作为缓和曲线用于保证车辆运行的安全与平顺。因此,在线状工程施工之前我们需要对带有缓和曲线的曲线进行测设。曲线测设的方法有很多种,例如偏角法、切线支距法、自由设站极坐标法等。而随着光电测距仪和全站仪的广泛实用,自由设站极坐标法在曲线测设中发挥了极大的作用,不仅降低了原先的工作量,而且大大提升了测设精度,并以此在线状工程曲线测设中得到了普及。自由设站极坐标法是把线状工程的直线段、圆曲线段和缓和曲线段组合成的曲线通过坐标转换归算到同一的导线测量坐标系统中,便可计算放样元素。而本文在自由设站极坐标法的基础上,通过对缓和曲线和圆曲线的性质分析,建立了三角形几何数学模型,减少原先自由设站极坐标法的坐标转换工作,且在圆心上设站仍然能够计算出曲线放样元素的方法。本文对圆心设站测设曲线的原理进行了分析,建立了数学模型,并详解运用一实例采用该方法完成了对曲线中线的测设。
2 圆心设站偏角法测设曲线的原理
任意设站偏角法与极坐标法同一个原理。极坐标的原理,如图1,A、B为已知点,P为放样点,其设计坐标已知,在A点架设经纬仪或全站仪,放样一个角β,定出方向AC。然后在这个方向距离放样s(AP的距离为s)便得到P点的实际位置。通过极坐标法原理可以知道极坐标法有两个要素,一个是角度,一个是距离,我们称之为极角和极距。和极坐标法一样,偏角法也有和它相同的两个要素,圆心设站法的极角μi是指以圆心O与ZH(0′)点的连线O′O与曲线上任意一点Pi到圆心O连线间的一个夹角;极距di是指曲线上任意一点Pi到圆心0连线的距离(如图2)。如果能够通过一定的数学几何关系,计算确定Pi点的极角和极距,我们便能通过圆心设站将Pi点的位置确定下来。
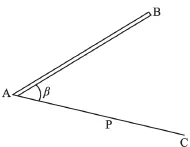
图1 极坐标放样法

图2 缓和曲线上任意一点在其切线坐标系中的位置
3 数学模型
3.1 第一缓和曲线的放样元素计算
图2中,缓和曲线(螺旋线)以ZH点为原点O′,以其切线为X′轴,Y′轴垂直于X′,使得两坐标轴将曲线夹在中间,构成X′O′Y′切线坐标系,设li为曲线任意一点Pi的弧长,如图2所示。
设缓和曲线任意一点Pi的坐标为x′iy′i则由文献[3]得:
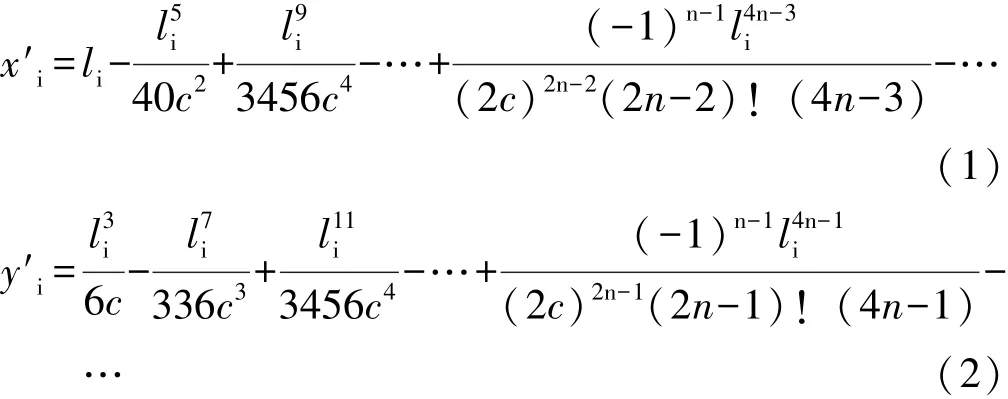
图3中由式(1)、式(2)及勾股定理得在缓和曲线上任意一点到ZH点的弦长长度为:


图3 带有缓和曲线的曲线测设

注:c=Rl0为缓和曲线参数,R为圆曲线半径,l0为缓和曲线长度;δi是指距缓和曲线起点为li的缓和曲线上一点Pi的旋切角。x′iy′i坐标公式中的n根据实际情况进行取值,一般全站仪放样距离时,考虑其他因素的影响,放样距离应控制在500 m以内,则n取值不会太大,一般为n=1,2,3。
则在△GVO中由余弦公式得:

再由正弦公式得:
∠OGV=arcsin{OV/GO·sin[(180°-α)/2]}
易知,ηI=∠OG Pi=∠OGV-δI
由△OGP,由余弦公式得:

则,μi=arcsin(GPi·sinηi/OPi)
其中GV=T为曲线切线长,α为转向角都为已知数据;μi为极角,di为极距。
3.2 第一节圆曲线HY点到QZ点的放样元素计算
根据四边形内角和为360°可知:
∠GO(HY)=[360°-(180°-α)-2∠OGV-(α-2β0)]/2=90°-∠OGV+β0
则在圆曲线上的点的极角为:∠GO(HY)加上其在圆曲线上的弧长所对应的圆心角之和。设li为圆曲线上任意一点Pi到ZH(HZ)点的弧长,则其极角为:
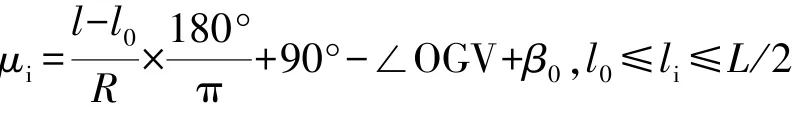
其中α-2β0为圆曲线的总圆心角。
而在圆曲线上的任意点的极距易知为圆曲线的半径长,则极距为:di=OPi=R
其中,l0为缓和曲线长,L为曲线总长度,β0缓和曲线切线角。
3.3 其他部分曲线放样元素计算
其他部分曲线测设包括第二节圆曲线(QZ点到YH点)和第二缓和曲线的测设,该部分的测设方法以HZ点为后视点,放样元素与第一缓和曲线和第一圆曲线的放样元素相同,只是放样角度时,转向相反,在此不用阐述。
4 圆心设站法对现场条件的要求
圆心设站法在测设过程中应当考虑设计道路在现场的具体环境。虽然圆心设站测设曲线避免了其他测设方法的过多设站和重复置镜后视点的工作,但正是如此,圆心设站法一次设站测设曲线只能在圆心上设站的单一性使得它对现场条件有一定的要求。
在施工现场中,圆心点的位置处于河流、沼泽、农田等导致无法在该点架站的条件下,不应当考虑此法。另外在参考文献[7]中作者提出采用标称精度2 mm+2 ppm,2″的全站仪,考虑到精度问题,理想的放样距离应控制在500 m以内。因此为了避免曲线过长造成圆心设站法极距的过大(最大的极距为圆心到直缓点和缓直点间的距离),圆心设站法仅适用于最大极距小于等于500 m的曲线测设。对于极距大于500 m带有缓和曲线的长大曲线,应采取其他测设方法。而为了能够在圆心架站一次性测设完曲线,应考虑到圆心前方通视(如图3ZH-O-HZ-YH-QZ-HY闭合区域)或者障碍物高度不能超过仪器中心到棱镜杆高为5 m时棱镜中心间的视线,如图4所示。

图4 圆心设站法现场条件要求
排除以上3个施工现场条件对圆心设站法测设曲线的影响,该方法将得以实施,并能更好地发挥其优势,简单快速完成曲线的测设。
5 运用实例
某公路有一带缓和曲线的曲线线路R=250 m,l= 63 m,α=46°34′52″,ZH点里程K101+137.89 m(如图5),运用圆心设站测设曲线法求曲线上每隔20 m一个细部点的放样要素和详细测设方法。

图5 圆心设站法运用实例
5.1 曲线要素和参数计算
曲线要素包括圆曲线要素和缓和曲线参数,圆曲线要素有:切线长T,曲线长L,曲线外矢距E,切曲差q;缓和曲线参数有:切垂距m,圆曲线内移值P,缓和曲线切线角β0,其计算结果分别为:
切曲差:q=2T-L=12.524 m
5.2 曲线放样元素计算结果
根据上述推导公式得出该带有缓和曲线的曲线每隔20 m一个细部点的放样要素,在坐标公式中,取n= 2,则细部点放样要素计算数据如表1和表2所示。
从上述计算所得的HY点放样数据与理论数据中进行比较,极角较差为∠OG(HY)=14°22′40″-14°22′41″=-1″,距离较差为R=250-250.00004= -0.00004 m,两者的较差都很小,应属于数据计算时位数取舍原因造成的,因此两者较差的大小可作为检验放样数据是否合格的依据,如果较差太大应重新计算直到与理论数据几乎相同,才可进行实际的曲线测设。而在对主点HY点和YH点时,为了减小计算误差带来的影响,应将其测设数据归为理论值,如上述例子中,HY点放样是极距应为圆曲线的半径长250 m;极角应为14°22′40″,而不是通过余弦定理和反三角函数所得到的14°22′41″。

第一缓和曲线放样元素 表1

第一节圆曲线放样元素 表2
注:铺助计算数据∠OGV=82°50′21″,GO=252.631m,∠OG(HY)=14°22′40″
5.3 圆心的测设
对于圆心的测设,有多种办法进行,选取两种作为说明。一是在JD点架设仪器,后视ZH点,左转(180° -α)/2(曲线是左偏情况)或右转(180°-α)/2(曲线为右偏情况),然后距离放样R+E,便可得到圆心点;第二种在ZH点架设仪器,后视JD点,右转角度∠OGV(曲线为右偏情况)或左转角度∠OGV(曲线为左偏情况),然后距离放样GO便可得到圆心,GO的长度和∠OGV可通过上述计算所得。
5.4 曲线的测设
圆心点位置确定下来之后,在其上面架设全站仪,后视ZH点作为零方向,对于第一部分曲线,只需拔角各个细部点的极距(曲线右偏,则左拔角,左偏则右拔角),确定放样方向后,再距离放样各个细部点的极角,便可得到包括主点在内的各个细部点的位置。对于第二部分的曲线放样数据测设方法与第一部分曲线放样相同,只是需后视HZ点作为零方向;另外曲线右偏,则右拔角,左偏则左拔角便可得到剩余主点及各个细部点的位置完成曲线中线的测设。
6 结 论
本文给出了圆心设站测设曲线的方法及原理,且实例表明该方法具有以下优点:
(1)该方法的放样元素数据计算简单,也可通过计算机编程计算得出,降低了数据计算的工作量,也确保了数据的准确性;
(2)采用该方法,各个细部点的极角、极距互不相关,因此误差不累计,特别是在测设圆曲线时角度方向误差不影响测设结果;
(3)该方法解决了因地形条件影响,不能在ZH (HZ)点或JD点架设仪器的问题;
(4)圆心设站测设曲线计算简单,不搬站,且快速,但考虑到圆心设站法对现场条件有一定的限制性,因此该方法适用于视野开阔,地势平坦的铁路和公路曲线测设中。
[1] 张正禄,李广云,潘国荣等.工程测量学[M].武汉:武汉大学出版社,2005(2).
[2] 彭仪普.任意站极坐标法测设线路平面曲线探讨[J].铁道工程学报,2001(3):11~13.
[3] 谯生有.缓和曲线坐标计算误差分析[J].测绘通报,2001(11):38.
[4] 张玲玲.高速公路互通式立交桥卵形曲线匝道的坐标计算方法[J].公路交通科技,2011,28(12):123~126.
[5] 杨存吉,李全信.线路中线测设的统一数学模型[J].测绘通报,2001(2):14~15.
[6] 高利平,刘霖,林敏等.带缓和曲线的长大曲线实用测设方法研究[J].中国公路学报,2002,15(4):25~27.
[7] 赵一飞.极坐标法放样公路中线的精度保证[J].交通科技,2003(4):34~35.
[8] 郭宗河,郑进风,朱亚光.特殊情况下缓和曲线的测设[J].测绘通报,2003(6):65~66.
[9] 周万枝,李菊霞.全站仪自由设站法道路定测[J].测绘通报,1998(10):37~38.
[10] 张还在.全站仪测设公路平曲线的精度分析[J].内蒙古交通运输,2008(2):17~19.
Study of Practical M ethod for Survey and Design the Curve on the Center
Luo Qingsong,Luo Yaodong
(Institute of Environment and Resource,Southwest University of Science and Technology,Mianyang 621010,China)
Curved road engineering generally require additional transition curve and circular curve as a link to the straight line road each other,its detailed surveying and designing commonly used polar coordinatemethod for free station positioning.On the basis of polar coordinatemethod for free station positioning to survey and design the curve,Considering the special nature of the center of circular curve,Established a feasibility mathematicalmodel for using deflection angle method for the Continuous setting out the curvewith the transition curves and analysis of its principles and surveymethod .By verifying the practicality and feasibility of themethod through an example,it is proved that themethod is simple calculation,and its survey and design process is simple,fast,practical and applicable to the construction site.
arrangement of curve;survey on the center;transition curve;circle curve;mathematicalmodel
1672-8262(2013)03-146-04
U412.245,P258
A
2012—09—04
罗清松(1990—),男,本科生,主要研究方向:工程测量。

