相干两点源角欺骗干扰的极化鉴别方法研究

李永祯，胡万秋，程旭，宗志伟，王雪松

(国防科学技术大学 电子信息系统复杂电磁环境效应国家重点实验室，湖南长沙410073)

0 引言

鉴于角度测量在目标跟踪、定位和制导中的重要性，寻求有效的角度欺骗干扰与抗干扰技术一直是雷达对抗研究的热点问题[1]。两点源角度欺骗干扰是目前使用最多的一种角度欺骗干扰，其本质是通过同时到达雷达接收天线的2 个不同方向的信源，使雷达角度测量出现偏差，进而破坏雷达角度跟踪[2－3]，其中相干两点源干扰由于可以使单脉冲雷达产生平台外的角度欺骗干扰效果而备受关注，其对抗方法的研究也正日益受到重视[3－8]。

目前，现有文献主要集中讨论了相干两点源角度欺骗干扰的基本原理[1，7]，可能的实现方式[9－10]以及相干两点源角度欺骗干扰效果的定量评估[11－13]等方面，而对相干两点源角度欺骗干扰的识别与抑制方面研究较少。极化描述了电磁波的矢量性，是幅度、频率、相位以外的1 个重要基本参量，极化信息的有效利用可以显著提高现代雷达的目标检测、抗干扰与目标识别能力。利用雷达目标和有源欺骗性电子干扰在极化特性上的差异进行真假鉴别与抑制方法的研究日益增多。文献[14]和文献[15]等设计了单极化有源假目标干扰的极化鉴别方法，研究结果表明，极化测量雷达可以以很高的概率鉴别复杂调制的单极化有源假目标。然而，极化信息用于角度欺骗干扰的鉴别与抑制方法尚甚少见诸报道。

随着数字射频存储器(DRFM)技术和相干干扰理论等的发展，相干两点源干扰已逐渐成为现实威胁。在此背景下，本文研究了利用极化信息进行识别相干两点源角度欺骗干扰的方法，给出了相干两点源干扰和雷达目标在单脉冲极化雷达测角系统中的不同极化通道响应函数，提出了一种相干两点源干扰存在的鉴别方法，理论分析和计算机仿真均证实了此算法的有效性。

1 相干两点源角度欺骗干扰原理

1.1 单脉冲雷达测角原理简析

电磁波在雷达接收天线上感应的开路电压[5]可表示为

式中:ei=[EiH，EiV]T为来波的电场矢量;h 为天线的有效接收矢量。有效接收矢量记为

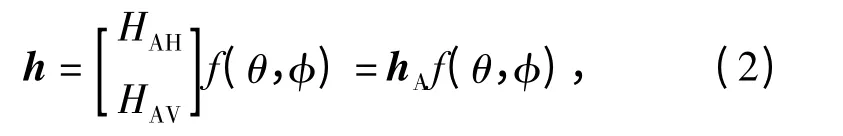
设单脉冲雷达天线波束1 和波束2 的电压方向图为f1(θ)= f(θ0－ θ)和f2(θ)= f(θ0+ θ)，θ0为2 个天线波束最大方向偏离天线瞄准方向的夹角，θ为来波偏离雷达视线(天线瞄准轴)的角度。那么，天线波束1 和波束2 的接收电压分别为

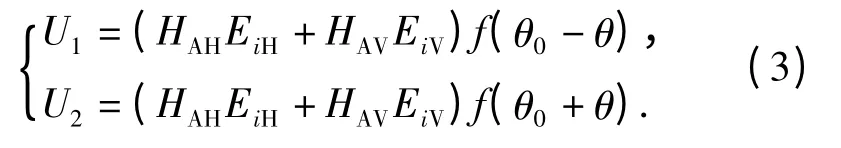
在不考虑接收噪声的情况下，对于幅度和差单脉冲测角体制雷达而言，根据角度鉴别公式，可得雷达角度的测量值为

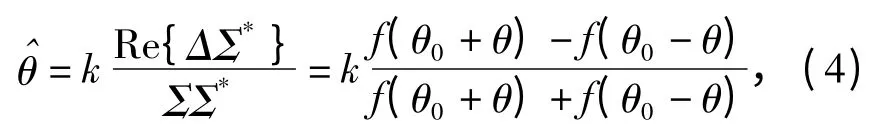
式中:Σ=U1+U2;Δ=U2－U1;k 为角度鉴别曲线斜率。

1.2 相干两点源角欺骗干扰的原理分析

由于雷达跟踪目标信号相位波前的法线方向，因此可以利用相干两点源在雷达天线口径内产生相位的不均匀性(即畸变的相位波前)，诱骗单脉冲雷达跟踪错位的方位。假定两干扰源到达雷达天线口面的信号具有稳定的相位关系，即有

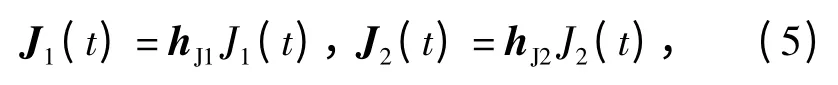
式中:hJ1=[HJH1，HJV1]T和hJ2=[HJH2，HJV2]T为两点干扰源辐射信号的极化方式，‖hJ1‖ =‖hJ2‖ =1(一般情况下，为了保证干扰信号在雷达天线口面具有稳定的相位关系，hJ1≈hJ2，且记为hJ=[HJH，HJV]T);J2(t)=βejφJ1(t)，φ 为两点源的相位差，β为两点源信号的幅度比。相干两点源干扰空间关系如图1 所示，其中:θ1为干扰源1 与瞄准轴的夹角，θ2为干扰源2 与瞄准轴的夹角。

图1 相干两点源干扰空间关系Fig.1 Space relation of coherent dual－source interference

雷达接收波束1、2 收到两干扰源的信号分别为

由(6)式可以得到和差波束信号，由于θ1和θ2均很小，有f(θ0±θ1)≈f(θ0)∓f'(θ0)θ1和f(θ0±θ2)≈f(θ0)∓f'(θ0)θ2成立，在此假设下，容易推得雷达的跟踪角[2，7]为

由(7)式可知，若能够对两点源的相对幅度和相对相位进行精确控制，则产生的线偏差值将非常大，从而达到非常好的干扰效果。

2 全极化雷达回波模型

2.1 相干两点源干扰的回波模型

极化雷达是利用极化状态正交的2 幅天线同时接收雷达目标散射的共极化分量和交叉极化分量，一般通过“轮流发射、同时接收”的模式获得目标的相干极化散射矩阵。

不妨设2 幅正交天线的极化状态分别为hA1=[1，0]T和hA2=[0，1]T，而电压方向图等其他特性均一致;因此，当雷达发射水平极化电磁波时，对于水平极化接收天线而言，相干两点源干扰的波束1和波束2 的接收信号分别为

因此，相干两点源干扰的和差波束回波信号分别为

式中:βH和φH为两点源的幅度比和相位差。

对于垂直极化接收天线而言，相干两点源干扰的和差波束回波信号分别为

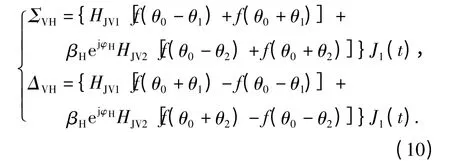
当hJ1=hJ2=hJ时，有

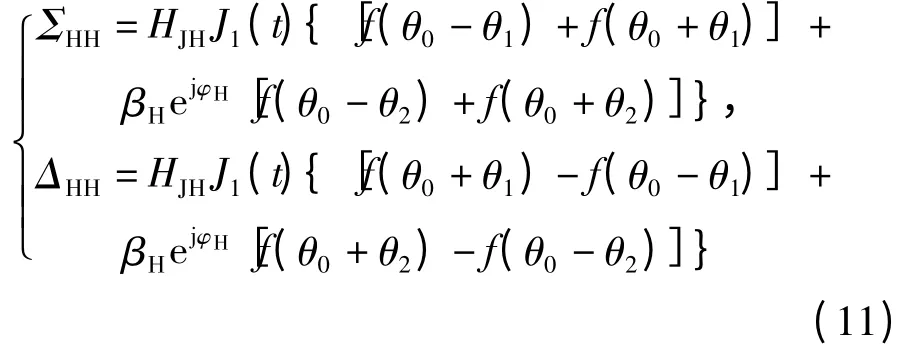
和

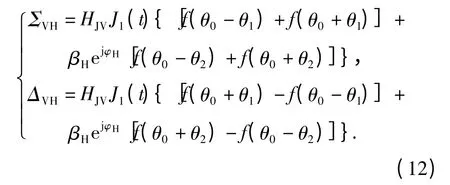
当在下一脉冲重复周期(τR)雷达发射垂直极化电磁波时，由于脉冲重复周期一般为毫秒量级，甚至更短，两点源干扰的极化方式可视为不变。对于水平极化接收天线而言，相干两点源干扰的波束1和波束2 的回波信号分别为

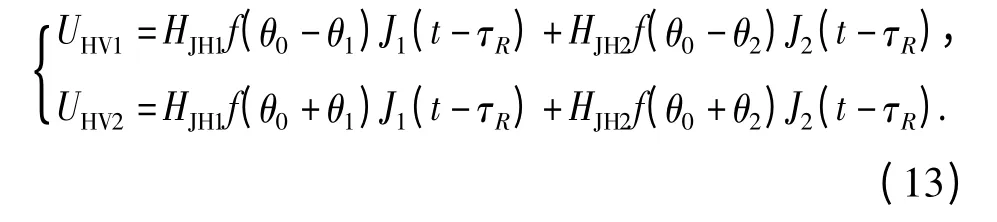
因此，相干两点源干扰的和差波束回波信号分别为

式中:βV和φV为此时刻两点源的幅度比和相位差。对于相干干扰而言，一般设计干扰信号的幅度比和相位差保持稳定，诸如交叉眼干扰，不妨设βH=βV和

对于垂直极化接收天线而言，易得相干两点源干扰的和差波束回波信号分别为

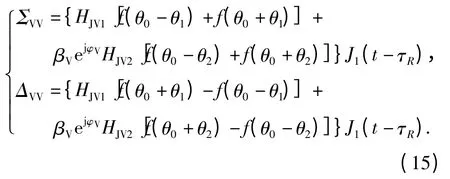
当hJ1=hJ2=hJ时，有

和

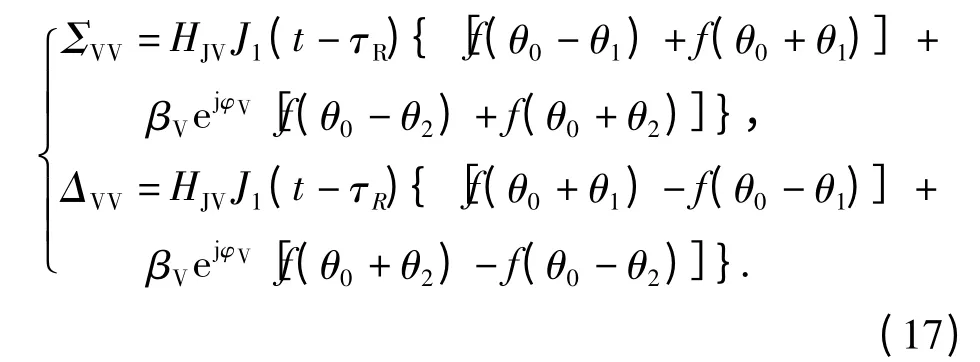
2.2 雷达目标的回波模型

式中:aejα为与雷达发射功率、天线增益、雷达与目标距离等因素有关的1 个常量因子;e(t)为雷达发射信号波形;θS为目标偏离雷达视线的角度。

对于垂直极化接收天线而言，雷达目标的和差通道信号分别为

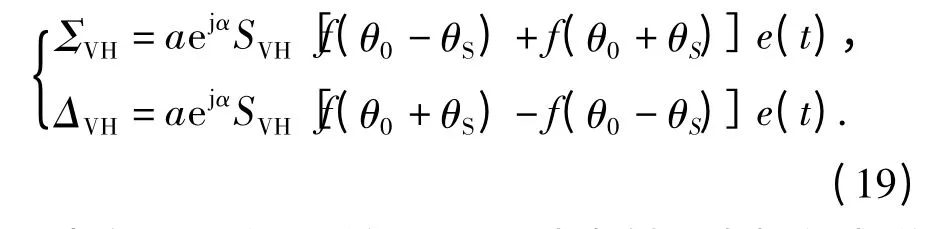
当在下一脉冲重复周期雷达发射垂直极化电磁波时，对于水平极化接收天线而言，雷达目标的和差通道信号分别为

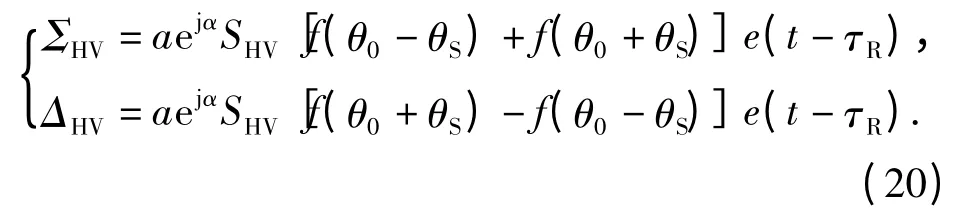
此时，对于垂直极化接收天线而言，雷达目标的和差通道信号分别为

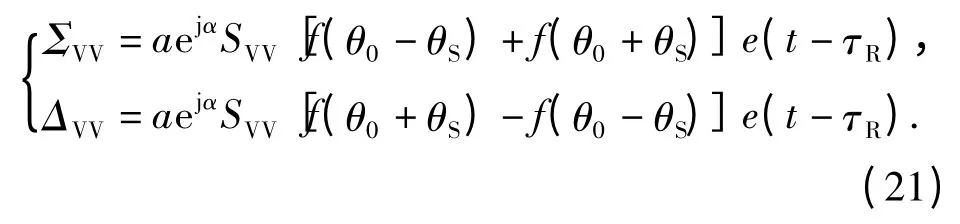
3 相干两点源干扰的极化鉴别方法

根据相干两点源干扰和雷达目标的全极化回波特性的差异，设计相干两点源干扰的极化鉴别方案。由(9)式和(10)式、(14)式和(15)式可得

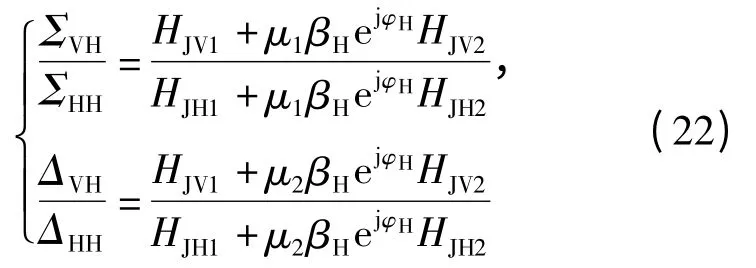
和

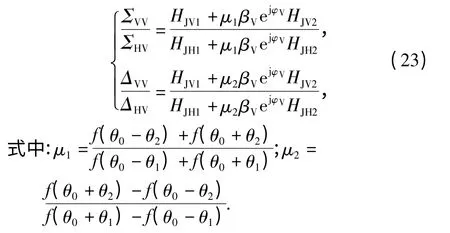
由(22)式和(23)式可得

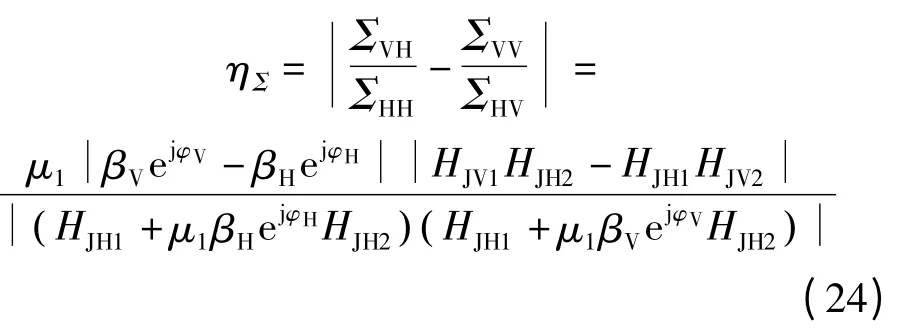
和

对于相干两点源干扰而言，一般有hJ1=hJ2，即HJV1HJH2－HJH1HJV2=0;另外，若幅度比和相位差保持稳定，满足βH=βV和φH=φV时，βVejφV－βHejφH=0;这也就是说，对于相干两点源干扰，在不考虑噪声的情况下ηΣ=ηΔ=0.

根据(18)式～(21)式，类似可推得

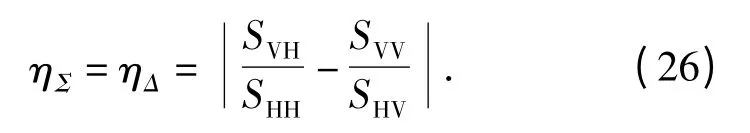
一般情况下，雷达目标的交叉极化分量比其主极化分量要小得多，即对于雷达目标而言，ηΣ=ηΔ＞1，这为判断是否存在两点源相干干扰提供了依据。因此可以按照以下二元假设检验进行判断:

式中:Th 为判决门限，由信噪比、雷达目标相干极化散射特性等共同决定的一个参量，结合典型弹头类和飞机类目标暗室测量数据的统计分析可知，在满足一定置信度水平的前提下，可设Th=1.

前文在没有考虑雷达系统噪声的情况下分析了鉴别检验量ηΣ的统计特性，以下将结合系统仿真给出实际欺骗干扰场景下ηΣ的统计结果。图2 ～图4给出了典型雷达目标的极化鉴别量的统计结果，采用数据为微波暗室测量数据，测量雷达中心频率为9 GHz，和波束的主瓣宽度为2°，雷达信号带宽5 MHz，脉冲重复周期0.6 ms，脉宽100 μs，被测目标位于雷达远场区。图5 给出了相干两点源角度欺骗干扰的极化鉴别量的统计分析结果，仿真选用的雷达工作频率与信号参数与暗室测量所用参数相同，干扰源位于单脉冲雷达的方位向平面内，相距100 m，两干扰源连线中心据雷达30 km.

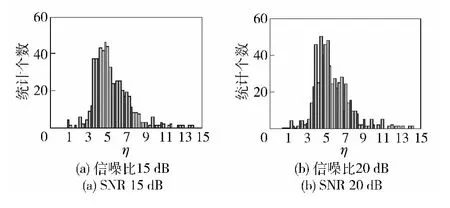
图2 某弹头目标模型极化鉴别量ηΣ 的统计结果Fig.2 Statistical results of polarization discriminating limen ηΣ of warhead target model

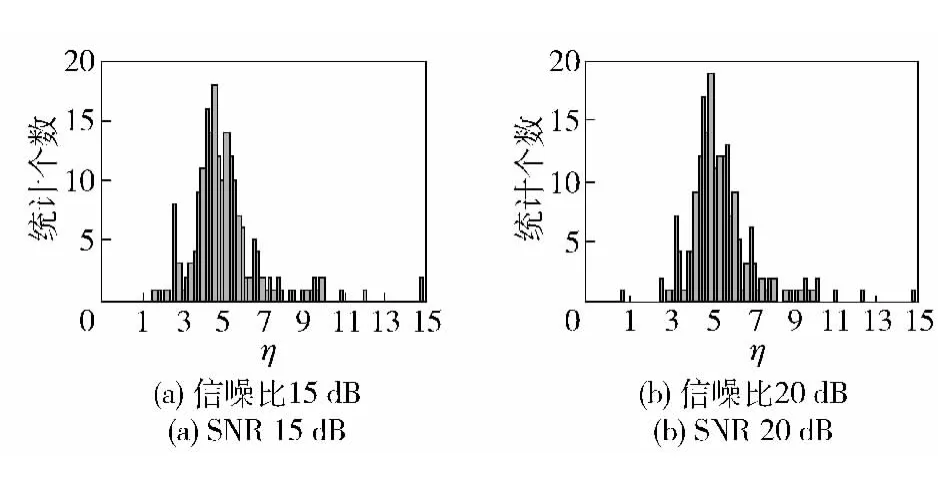
图3 锥球体目标极化鉴别量ηΣ 的统计结果(球直径d=0.140 m，锥体母线L=0.600 m)Fig.3 Statistical results of polarization discriminating limen ηΣ of taper and sphere targets (sphere d=0.140 m，taper L=0.600 m)

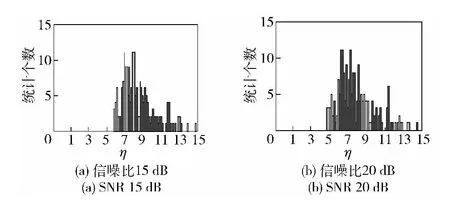
图4 开缝锥球体目标极化鉴别量ηΣ 的统计结果(球直径d=0.140 m，锥体母线L=0.600 m)Fig.4 Statistical results of a gap polarization discriminating limen ηΣ of taper and sphere targets (sphere d =0.140 m，taper L=0.600 m)

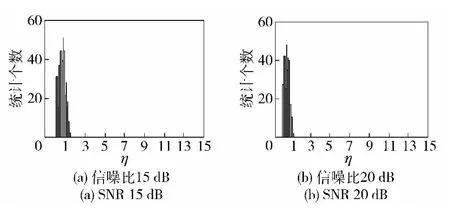
图5 相干两点源干扰的极化鉴别量ηΣ 的统计结果Fig.5 Statistical results of polarization discriminating limen ηΣ of coherent dual－source interference

通过图2 ～图5 及大量仿真结果可见，相干两点源干扰的极化鉴别量ηΣ远小于雷达目标的值，这表明了本文通过对极化鉴别量的检测判断存在相干两点源干扰的正确性。在判断出存在相干两点源干扰的情况下，可以根据具体场景来设计相应的干扰抑制方法，本文不再赘述。诸如对于反辐射应用背景，可以根据极化通道功率的大小，综合判断两点源回波强度的大小和其角度方向[16]，选择其中的1个进行跟踪(选择跟踪回波强度大的，或者回波强度小的);对于精确打击、防空反导等应用场景而言，若相干两点源中还有目标存在的话，可以采用切换复杂波形(诸如极化编码等)、极化滤波等方法滤除相干干扰源信号。

4 结论

本文根据雷达目标与相干两点源干扰的交叉极化分量与其主极化分量的相对大小关系，构建了鉴别典型目标与相干两点源干扰的极化鉴别量。通过对暗室测量结果及计算机仿真结果的分析发现，利用本文所提极化鉴别量可以有效地鉴别目标与相干两点源干扰，进一步说明了极化信息在目标鉴别方面具有显著优势。本文的研究工作对于雷达系统优化设计、干扰系统优化设计等应用领域有着一定的参考价值。

References)

[1]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社，1999:169 －182.ZHAO Guo－qing.Principle of radar countermeasures[M].Xi'an:Xidian University Press，1999:169 －182.(in Chinese)

[2]陈宁，蒋勇.相干两点源对单脉冲角跟踪诱偏方向的研究[J].电子对抗，2009，(3):6 －9.CHEN Ning，JIANG Yong.Study on coherent dual－source counter monopulse angle tracking direction[J].Aero Electronic Warfare，2009，(3):6 －9.(in Chinese)

[3]李雅博，白渭雄.精确制导武器对抗两点源干扰的技术研究[J].飞航导弹，2011，(7):88 －91.LI Ya－bo，BAI Wei－xiong.Study on precision guided weapon counter coherent dual－source[J].Aerodynamic Missile，2011，(7):88 －91.(in Chinese)

[4]杨文化，高梅国.反辐射导弹抗两点源干扰研究[J].航天电子对抗，2005，21(3):17 －19.YANG Wen－hua，GAO Mei－guo.Study on anti－radiation missle dual－source deception interference[J].Aero Electronic Warfare，2005，21(3):17 －19.(in Chinese)

[5]庄钊文，肖顺平，王雪松.雷达极化信息处理及其应用[M].北京:国防工业出版社，1999:93 －103.ZHUANG Zhao－wen，XIAO Shun－ping，WANG Xue－song.Radar polarization information processing and application[M].Beijing:National Defense Industry Press，1999:93 －103.(in Chinese)

[6]Giuli D，Fossi M，Facheris L.Radar target scattering matrix measurement through orthogonal signals[J].IEEE Proceedings－F，1993，140(4):233 －242.

[7]陈安娜.对单脉冲雷达的相干两点源干扰机理研究[J].航空兵器，2007，(2):7 －11.CHEN An－na.Study of monopulse radar coherent dual－source interference mechanism[J].Aero Weaponry，2007，(2):7 －11.(in Chinese)

[8]陆静，郭克成，张社欣.对反辐射导引头的欺骗干扰[J].雷达与对抗，2002，(2):40 － 47.LU Jing，GUO Ke－cheng，ZHANG She－xin.Cheat jamming to the antiradiation direct－head[J].Radar and Counteract，2002，(2):40 － 47.(in Chinese)

[9]司锡才，查玉峰.相干两点源抗反雷达导弹可能性研究[J].航天电子对抗，1988，(1):1 －19.SI Xi－cai，ZHA Yu－feng.The possiblity of coherent dual－source counter anti－radiation missle[J].Aero Electronic Warfare，1988，(1):1 －19.(in Chinese)

[10]李相平，赵腊，胡磊.相干两点源对反舰导弹导引头的干扰研究[J].制导与引信，2008，29(3):48 －52.LI Xiang－ping，ZHAO La，HU Lei.A study on the coherent dual point－source interference to the antiship missile seeker [J].Guidance ＆ Fuze，2008，29(3):48 －52.(in Chinese)

[11]Lian W J.Discussion of radar anti－radiation missile technology alarming plus decoy system，ADA310623[R].Dayton:National Air Intelligence Center，1996.

[12]史震，李岩，于秀萍.多点源作用下反辐射导弹导引信号的形成[J].哈尔滨工程大学学报，2006，27(1):70 －74.SHI Zhen ，LI Yan，YU Xiu－ping.Formation of guidance signal of anti－radiation missile under the action of multiple sources[J].Journal of Harbin Engineering University，2006，27(1):70 －74.(in Chinese)

[13]曲志昱，司锡才，谢纪岭.相干源诱偏下比相被动雷达导引头测角性能分析[J].系统工程与电子技术，2008，30(5):824 －827.QU Zhi－yu，SI Xi－cai，XIE Ji－ling.Analysis of phase－comparison passive－radar－seeker angle measurement with decoy of coherent source[J].Systems Engineering and Electronics，2008，30(5):824 －827.(in Chinese)

[14]李永祯.瞬态极化统计特性及处理的研究[D].长沙:国防科学技术大学，2004.LI Yong－zhen.Study on statistical characteristics and processing of instantaneous polarization[D].Changsha:National University of Defense Technology，2004.(in Chinese)

[15]施龙飞.雷达极化抗干扰技术研究[D].长沙:国防科学技术大学，2008.SHI Long－fei.Study on the suppression of interference with radar polarization information[D].Changsha:National University of Defense Technology，2008.(in Chinese)

[16]罗金亮，赵静静，张建科.单脉冲跟踪雷达抗双点源干扰研究[J].火控雷达技术，2009，38(3):22 －25.LUO Jin－liang，ZHAO Jing－jing，ZHANG Jian－ke.Study on monopulse tracking radar against counter double－point sources jamming[J].Fire Control Radar Technology，2009，38(3):22 －25.(in Chinese)